2. Задания по теме "Динамическое программирование"

Задание 4. Определить оптимальный цикл замены оборудования при исходных данных: Р = 13, S(t) = 0, f(t) = r(t) — u(t), представленных в таблице 2.

Таблица 2

N	0	1	2	3	4	5	6	7	8
f (t)	13	12	11	9	7	4	1	0	0

РЕШЕНИЕ.Функциональные уравнения, основанные на принципе оптимальности, для данного примера имеют вид:

Результаты расчетов помещаем в таблицу, момент замены отмечен звездочкой, после чего дальнейшие вычисления по строчке прекращаем (табл. 3).

Таблица 3

FN(t)	0	1	2	3	4	5	6	7	8
	N	N-1	7	6	5	4	3	2	1
f1 (t)	13	12	11	9	7	4	1	0	0
f2 (t)	25	23	20	16	13	5	5*
f3 (t)	36	32	27	22	22*
f4 (t)	45	39	33	28	28*
f5 (t)	52	45	39	39*
f6 (t)	58	51	50	48	46	43	43*
f7 (t)	64	62	59	55	50	50*
f8 (t)	75	71	66	59	59*
f9 (t)	84	78	70	70*

Вычисления продолжаем до тех пор, пока не будет выполнено условие f1(1) > f2(2), т.е. в данный момент оборудование необходимо заменить, так как величина прибыли, получаемая в результате замены оборудования, больше, чем в случае использования старого.

По результатам вычислений и по линии, разграничивающей области решений сохранения и замены оборудования, находим оптимальный цикл замены оборудования. Для данной задачи он составляет 3 года.

Ответ. Для получения максимальной прибыли от использования оборудования в восьмиэтапном процессе оптимальный цикл состоит в замене оборудования через каждые 3 года.

Задание 5. Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме. Для модернизации предприятий совет директоров инвестирует средства в объеме 250 млн р. с дискретностью 50 млн р. Прирост выпуска продукции зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таблице 4.

Таблица 4

Инвестиции, млн. р	Прирост выпуска продукции, млн. р.
	Предприятие 1	Предприятие 2	Предприятие 3	Предприятие 4
50	12	13	11	11
100	17	15	16	18
150	23	25	21	22
200	34	33	35	34
250	42	41	43	44

Найти распределение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить только одну инвестицию.

РЕШЕНИЕ. Разобьем решение задачи на четыре этапа по количеству предприятий, на которых предполагается осуществить инвестиции. Рекуррентные соотношения будут иметь вид:

• для предприятия № 1: f₁(x)=g₁(x)

• для всех остальных предприятий: f_k(x)= min{f _k(x_k) + f _k-1(x- x_k )}, k =

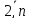
Решение будем проводить согласно рекуррентным соотношениям в четыре этапа.

1-й этап. Инвестиции производим только первому предприятию. Тогда

f₁(50) = 12, f₁(100) = 17, f₁(150) = 23, f₁(200) = 34, f₁(250) = 42.

2-й этап. Инвестиции выделяем первому и второму предприятиям. Рекуррентное соотношение для 2-го этапа: f₂(x)= max {g₂(x₂) + f₁ (x- x₂ )}

Тогда

при х = 50 f₂(50) = max (12 + 0,0 + 13) = max (12, 13) = 13,

при x = 100 f₂(100) = max (17,12 + 13,15) = max (17, 25, 15) =25,

при х = 150 f₂(150) = max (23,17 + 13, 12 + 15,25) = max (23,30, 27,25) =30,

при х = 200 f₂(200) = max (34,23 + 13,17 + 15,12 + 25,33) = max (34, 36, 32, 37, 33) = 37,

при х = 250 f₂(250) = max (42,34 + 13,23 + 15,17 + 25,12+ 33,41) = max (42, 47, 38, 42, 45, 41) = 47.

3-й этап. Финансируем 2-й этап и третье предприятие. Расчеты проводим по формуле F₂(x)= max {g₃(x₃) + f₂ (x- x₃)}

Тогда

при х = 50 f₃(50) = max (13, 11) = 13,

при x = 100 f₃(100) = max (15,13 + 11,16) = max (15, 24, 16) =24,

при х = 150 f₃(150) = max (25,15+ 11, 13 + 16,21) = max (25,26, 29,21) =29,

при х = 200 f₃(200) = max (33,25 + 11,15 + 16,13+ 21,35) = max (33, 36, 31, 33, 35) = 36,

при х = 250 f₃(250) = max (41,33 + 11,25 + 16,15 + 21,13+ 35,43) = max (41, 44, 41, 36, 48, 43) = 48.

4-й этап. . Финансируем 3-й этап и четвертое предприятие. Расчеты проводим по формуле F₄(x)= max {g₄(x₄) + f₃ (x- x₄)}

Тогда

при х = 50 f₄(50) = max (11, 11) = 11,

при x = 100 f₄(100) = max (16,11 + 11,18) = max (16, 22, 18) =22,

при х = 150 f₄(150) = max (21,16+ 11, 11 + 18,22) = max (21,27, 29,22) =29,

при х = 200 f₄(200) = max (35,21 + 11,18 + 16,22+ 11,34) = max (33, 32, 34, 33, 34) = 34,

При х = 250 f₄(250) = max (43,35 + 11,21 + 18,16 + 22,11+ 34,44) = max (43, 46, 39, 38, 45, 44) = 46.

Получены условия управления от 1-го до 4-го этапа. Вернемся от 4-го к 1-му этапу. Максимальный прирост выпуска продукции в 48 млн р. получен на 3-м этапе как 13 + 35, т.е. 13 млн р. соответствуют выделению 50 млн р. третьему предприятию. Согласно 2-му этапу 37 млн р. соответствует выделению 200 млн р. второму предприятию. Таким образом, инвестиции в объеме 250 млн р. целесообразно выделить второму и третьему предприятиям по 200 и 50 млн р. соответственно, при этом прирост продукции будет максимальным и составит 50 млн р.

Задание 6. В трех районах города предприниматель планирует строительство пользующихся спросом одинаковых по площади мини-магазинов "Продукты". Известны места, в которых их можно построить. Подсчитаны затраты на их

строительство и эксплуатацию. Необходимо так разместить мини-магазины, чтобы затраты на их строительство и эксплуатацию были минимальные.

x	1	2	3	4
g1(x), ден. ед.	8	13	21	28
g2(x), ден. ед.	9	14	20	27
g3(x), ден. ед.	7	15	22	30

В данном примере gi(х) — функция расходов в ден. ед., характеризующая величину затрат на строительство и эксплуатацию в зависимости от количества размещаемых предприятий в i-м районе; φk(x) — наименьшая величина затрат в млн. р., которые нужно произвести при строительстве и эксплуатации предприятий в первых k районах.

РЕШЕНИЕ. Решение задачи проводим с использованием рекуррентных соотношений: для первого района: φ₁(x)=g₁(x)

для остальных районов: φ _k(x)= min{φ _k(x_k) + φ _k-1(x- x_k )}, k =

Задачу будем решать в три этапа.

1-й этап.

φ₁(1)=g₁(1)=8, φ₁(2)=g₁(2)=13, φ₁(3)=g₁(3)=21, φ₁(4)=g₁(4)=28

Если все предприятия построить только в первом районе, то минимально возможные затраты при х = 4 составляют 28 млн р.

2-й этап. Определим оптимальную стратегию при размещении предприятий только в первых двух районах по формуле φ ₂(x)= min{φ ₂(x₂) + φ _2-1(x- x₂ )}

Найдем φ₂(l):

g₂(1) + φ₁(0) = 9 + 0 = 9, g₂(0) + φ₁(l)= 0 +8 = 8, φ₂(l) = min (9, 8) = 8.

Вычислим φ₂(2):

g₂(2) + φ₁(0) = 14 + 0 = 14, g₂(l) + φ₁(l) = 9 + 13 = 22, g₂(0) + φ₁ (2) = 0 + 13 = 13, φ₂(2) = min (14, 22, 13) = 13.

Найдем φ₂(3):

g₂(3) + φ₁ (0) = 20 + 0 = 20, g₂(2) + φ₁(l) = 14 + 8 = 22, g₂(1) + φ₁(2) = 9 + 13 = 22, g₂(0) + φ₁(3) = 0 + 21= 21, φ₂(3) = min (20, 22, 22, 21) = 20.

Определим φ₂(4):

g₂(4) + φ₁(0) = 27 + 0 = 27, g₂(3) + φ₁(l) = 20 + 8 = 28, g₂(2) + φ₁(2) = 14 + 13 = 27, g₂(l) + φ₁(3) = 9 + 21 = 30, g₂(0) +φ₁(4) = 0 + 28 = 28, φ₂(4) = min (27, 28, 27, 30, 28) = 27.

3-й этап. Определим оптимальную стратегию при размещении пяти предприятий в трех районах по формуле φ₃(x) = min{g₃(x3) + φ₂(x – х₃)}.

Найдем φ₃(4):

g₃(4) + φ₂(0) = 30 +0 = 30, g₃(3) + φ₂(1) = 22 + 8 = 30, g₃(2) +φ₂(2) = 15 + 13 = 28, g₃(1) + φ₂(3) = 7 + 20 = 27, g₃(0) + φ₂(4) = 27 + 0 = 27, φ₃(5) = min (30, 30, 27, 27) = 27.

Минимально возможные затраты при х = 4 составляют 27 ден. ед. Определены затраты на строительство предприятий от 1-го до 3-го этапа. Вернемся от 3-го к 1-му этапу. Минимальные затраты в 27 ден. ед. на 3-м этапе получены как 7 + 20, т.е. 7 ден. ед. соответствуют строительству одного предприятия в третьем районе. Согласно 2-му этапу 27 ден. ед. получены как 13 + 14, т.е. ден. ед. соответствуют строительству двух предприятий во втором районе.

Ответ. Оптимальная стратегия состоит в строительстве трех предприятий во втором и одного предприятия в третьем районе, при этом минимальная стоимость строительства и эксплуатации составит 47 ден. ед.