Лекции по Матанализу ч1

Теория пределов функции одной переменной.

Предел числовой последовательности.

Определение. Если каждому натуральному числу n поставлено в соответствие число xn , то говорят, что задана последовательность xn

xn x1, x2 , , xn ,

Общий элемент последовательности является функцией от n . xn f xn

Таким образом, последовательность может рассматриваться как функция. Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример.

xn 1 n 1,1, 1,1,

x		sin	n	1,0, 1,0,1,0, 1,0
n
			2

Для последовательностей можно определить следующие операции:

1)Умножение последовательности на число m : m xn mxn mx1, mx2 ,

2)Сложение (вычитание) последовательностей: xn yn xn yn .

3)Произведение последовательностей: xn yn xn yn .

	x	n		x		n			yn 0 n .
4) Частное последовательностей:								при
	yn
				yn

Ограниченные и неограниченные последовательности.

Определение. Последовательность xn называется ограниченной, если существует такое число M 0 , что для любого n верно неравенство:

xn M

т.е. все члены последовательности принадлежат промежутку M , M .

Определение. Последовательность xn называется ограниченной сверху, если для любого n существует такое число M , что

xn M .

Определение. Последовательность xn называется ограниченной снизу, если для любого n существует такое число M , что

					xn M
Пример. xn n – ограничена снизу {1, 2, 3, … }.
Определение.	Число a называется пределом последовательности xn ,
0 N : n N			xn a

Это записывается: lim xn a .

n

В этом случае говорят, что последовательность xn сходится к a при n .

Свойство: Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim ( 1)n 0 . n

21

	Пусть при n N верно	0	( 1)n	, т.е.	1	. Это верно при	n	1	, таким
			n		n

образом, если		за N		взять целую часть от			1		,		то утверждение,								приведенное
выполняется.
Пример. Показать, что при n последовательность 3, 2																	1	, 2	1	, 2	1	,..., 2		1
																2			3		4			n
пределом число 2.
Итого: x		2	1		1	x 2
	n
			n		n	n
															1
Очевидно, что существует такое число n, что										x	n	2				, т.е. lim x							2 .
															n				n		n

выше,

имеет

Теорема. Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность xn имеет два предела a и b,

не равные друг другу.

xn a ; xn b ;

a b .

Тогда по определению существует такое число >0, что

a x

,

b x

n

2

n

2

Запишем выражение:

a b

(a xn )

(xn b)

a xn

xn

b

2

2

А т.к. - любое число, то

a b

0 , т.е. a b . Теорема доказана.

Следствие. (Достаточное условие расходимости последовательности) Если из последовательности можно выделить две подпоследовательности с разными пределами, то эта последовательность расходится.

Пример. xn 1 n . Имеем

x2k 1

lim x2k 1

k

x2k 1 1

lim x2k

1

k

Таким образом, данная последовательность расходится.

Теорема. Если xn a ,

то

xn

a

.

Доказательство. Из xn a следует, что

xn

a

. В то же время:

xn

a

xn a

, т.е.

xn

a

, т.е.

xn

a

. Теорема доказана.

Теорема. Если xn a , то последовательность xn ограничена.

Замечание. Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

			1
	1					, при четном n
			n
Например, последовательность xn			1			не имеет предела, хотя
	2					, при нечетном n
				n

xn 2.

Монотонные последовательности.

Определение. 1) Если xn 1 xn для всех n , то последовательность возрастающая. 2)Если xn 1 xn для всех n, то последовательность неубывающая.

22

3)Если xn 1 xn для всех n, то последовательность убывающая. 4)Если xn 1 xn для всех n, то последовательность невозрастающая

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Пример. xn 1n – убывающая и ограниченная

xn n – возрастающая и неограниченная.

Пример. Доказать, что последовательность xn

n

монотонная возрастающая.

2n 1

Найдем член последовательности x

n 1

n 1

n 1

2n 2 1

2n 3

Найдем знак разности:

x x

n

n 1

2n2 3n 2n2 2n n 1

1

0

n 1

n

2n 1

2n 3

(2n 1)(2n 3)

(2n 1)(2n 3)

т.к. n N ,

то знаменатель

положительный

при

любом n. Таким

образом, xn 1 xn .

Последовательность возрастающая, что и следовало доказать.

Пример. Выяснить является возрастающей или убывающей последовательность

x

n

.

n

5n

Найдем x

n 1

. Найдем разность

x

x

n 1

n

n 1 5n

n 1

5n 1

n 1

n

5

5n

5n

5 5n

1 4n , т.к. n N , то 1 – 4n <0, т.е. xn 1 xn . Последовательность монотонно убывает.

5 5n

Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.

Теорема Вейрштрасса. Монотонная ограниченная последовательность имеет предел.

Доказательство. Рассмотрим монотонную неубывающую последовательность

	x1 x2 xn xn 1
Эта последовательность ограничена сверху:						xn M , где M – некоторое число.
Т.к. любое, ограниченное сверху, числовое множество имеет четкую верхнюю грань,
то 0 N :	xN a , где a – некоторая верхняя грань множества.
Т.к. xn - неубывающая последовательность,								то при	N n a xN xn , т.е.
xn a
Отсюда a xn a или			a xn		. ,	т.е. lim xn			a
								n
Для остальных монотонных последовательностей доказательство аналогично.
Теорема доказана.
			Число е.
							1	n
Рассмотрим последовательность xn : xn 1								.
Если последовательность xn							n
		монотонная и ограниченная, то она имеет конечный

предел. По формуле бинома Ньютона:

23

				1	n								n				1							n(n 1)									1								2					n(n 1)(n 2)																						1 3										n(n 1)(n 2)...[n (n 1)]																									1 n
1								1																																																															...																																		и
																										1 2																									1 2 3																															1 2 3 n
				n								1					n																n																																	n																																				n
ли, что то же самое
x			1 1						1		1							1					...								1		1							1			1							2		... 1								k 1									...						1		1			1		1					2			... 1					n 1
	n
																																																																																																n
									2!									n													k!									n										n												n													n!					n							n
					Покажем,														что последовательность																																						xn – возрастающая. Действительно, запишем
выражение xn 1 и сравним его с выражением xn :
	x				1 1								1			1									1					...								1				1							1					1				2										... 1						k 1					...				1		1							1		1							2			...
			n 1
													2!									n 1															k!											n 1											n 1															n 1									n!								n 1										n 1
	... 1					n 1											1									1				1						... 1													n				.
																															n
						n 1									(n 1)!																			1													n		1
					Каждое слагаемое в выражении xn 1																																																				больше соответствующего значения xn , и, кроме
того,					у			члена									xn 1									добавляется																			еще								одно							положительное																				слагаемое.												Таким									образом,
последовательность																									xn возрастающая.
					Докажем теперь, что при любом n ее члены не превосходят трех: xn 3 .
																																																																																1			1
																				1							1												1																1			1														1											2n											1
					x			1 1																					...													1 1																								...											1												1										3
							n																																																																	2n 1																						1
																			2! 3!																			n!															2 22																														1
																																																																																	1											1
																																																																																				2												2
																																																					1				n
					Итак,								последовательность																																1													-					монотонно															возрастающая														и			ограниченная
																																																					n
сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой e .
																																																											1 n
																																																			lim 1																	e
																																																			n								n
																																1		n					3						следует, что e 3 . Отбрасывая в равенстве для xn все
					Из неравенства 1
																																	n
члены, начиная с четвертого, имеем:
																																																			1		n										1								1
																																												1													2											1
																																																			n												2								n
переходя к пределу, получаем
																																																			e 2								1				2,5
																																																										2

Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа e .

Можно показать, что число е иррациональное и его значение равно 2,718281828459045…

24

f x

Предел функции в точке.

Пусть функция f x определена в некоторой проколотой окрестности точки x a (т.е. в самой точке x a функция может быть и не определена)

Определение. (предел функции по Коши) Число А называется пределом функции

f x при x a , если для любого >0 существует такое число 0 , что для всех x

таких,

что 0

x a

верно неравенство

f x A

, т.е.

0 : из

x a

f x A

(1)

То же определение может быть записано в другом виде:

Если a x a , x a , то верно неравенство A f x A .

Запись предела функции в точке: lim f (x) A

f x A1

x a

Определение.

Если

при x a только при

x a ,

то

lim

f (x) A1 -

x a 0

называется пределом функции f x

в точке x a слева, а

если f x A2

при

x a

только при x a , то

lim

f (x) A2

называется пределом функции

f x

в точке

x a

x a 0

справа.

Запишем сказанное на языке :

lim f (x) A1 0 : из 0 a x

f x f a

x a 0

Приведенное выше определение относится к случаю, когда функция не

определена в самой точке x a , но определена в некоторой сколь угодно малой окрестности этой точки.

25

Пределы A1 и A2 называются также односторонними пределами функции f x в точке x a . Также говорят, что A – конечный предел функции f x .

Теорема о связи между пределом и односторонними пределами. Для того, чтобы функция f x имела в точке x a предел равный A необходимо и достаточно, чтобы в

этой точке существовали одновременно оба равных между собою односторонних предела, т.е.

lim

f (x) A

lim f (x) A

x a a

f (x) A

x a

lim

x a a

Доказательство. Необходимость. Из существования предела в точке x a следует

что

f x A

из 0

x a

Но первое неравенство можно записать в виде системы

из 0

x a

0 x a ,

x a

a x ,

x a

0

откуда получаем существование двух равных односторонних переделов. Очевидно, по той же причине верно и обратное утверждение.

В ряде случаев, удобно использовать другое определение предела функции. Идея этого определения заключается в том, что предел функции сводится к пределу последовательности.

f x

Определение. (предел функции по Гёйне) Число

A называется пределом функции

в точке x a если она определена в некоторой O a

и для любой последовательности

xn ,

такой что

xn O a n N соответствующая последовательность значений функции

f xn сходится к числу A , т.е.

0 и N : n N из

xn a

f xn A

(2)

Теорема. Определение предела функции по Коши и по Гейне эквивалентны.

Доказательство. То, что из существования предела по Коши следует существование

предела по Гёйне очевидно, т.к. условие (1) жёстче условия (2).

Докажем, что из существования предела по Гёйне следует существование предела по

Коши. Предположим обратное, тогда

f xn A

a

0

0 : xn : из

xn

В частности, можно считать, что

из

xn

a

f xn A

0

n

Из этого заключаем, что lim xn

a и при этом, число A не может быть пределом

n

f xn , поэтому, число

последовательности значений функции

A не является пределом

функции f x

в точке x a по Гёйне. Полученное противоречие доказывает утверждение

теоремы. Теорема доказана.

Предел функции при стремлении аргумента к бесконечности.

Определение. Число А называется пределом функции f x					при x , если для
любого числа >0	существует такое число M 0 , что для всех x ,					x		M выполняется
неравенство
		A f (x)

26

При этом предполагается, что	функция f x определена в окрестности
бесконечности. Записывают: lim f (x) A.	Графически можно представить:
x

Аналогично можно определить пределы lim f (x) A для любого		x M и
	x
lim f (x) A для любого	x M .
x

Бесконечно малые функции.

Определение. Функция f x называется бесконечно малой при x a , где а может

быть числом или одной из величин ( + или -) если lim f (x) 0 .

x a

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример. Функция f x xn является бесконечно малой при x 0 и не является

бесконечно малой при x 1 , т.к. lim f (x) 1.

x 1

Теорема. Для того, чтобы функция f x при x a имела предел, равный А,

необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f x A x ,

где x – бесконечно малая при x a ( x 0 при x a ).

Свойства бесконечно малых функций:

1)Сумма фиксированного числа бесконечно малых функций при x a тоже бесконечно малая функция при x a .

2)Произведение фиксированного числа бесконечно малых функций при x a тоже бесконечно малая функция при x a .

3)Произведение бесконечно малой функции на функцию, ограниченную вблизи точки x a является бесконечно малой функцией при x a .

4)Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю, есть величина бесконечно малая.

27

Основные теоремы о пределах.

Теорема 1. lim C C , где С = const.

x a

f x и

g x

Следующие теоремы справедливы при предположении,

что функции

имеют конечные пределы при x a .

Теорема 2. lim( f (x) g(x)) lim f (x) lim g(x)

x a

x a

x a

Доказательство. Представим f x A x ,

g x B

x , где

A lim f (x),

B lim g(x) , тогда

x a

x a

x g x A B x x

f

A B const ,

x x – бесконечно малая при x a , значит

lim( f (x) g(x)) A B lim f (x) lim g(x)

x a

x a

x a

Теорема доказана.

Теорема 3.

lim[ f (x) g(x)] lim f (x) lim g(x)

x a

x a

x a

Доказательство. Представим f x A x ,

g x B

x , где

A lim f (x),

B lim g(x) , тогда

x a

x a

f (x) g(x) A B A (x) (x)B (x) (x)

A B const ,

x x – бесконечно малая при x a , значит

lim[ f (x)g(x)] lim A B 0 A B lim f (x) lim g(x)

x a

x a

x a

x a

Теорема доказана.

Следствие.

lim C f (x) C lim f (x)

x a

x a

f (x)

lim f (x)

Теорема 4.

lim

x a

при lim g(x) 0

x a

g(x)

lim g(x)

x a

x a

Теорема 5. Если f x 0 вблизи точки x a и lim f (x) A , то A 0 .

x a

Аналогично определяется знак предела при

f x 0 ,

f x 0 , f x 0 .

Теорема 6. Если g x f x u x вблизи точки x a и lim g(x) lim u(x) A , то и

lim f x A .

x a

x a

x a

f x называется ограниченной вблизи точки

Определение.

Функция

x a ,

если

существует такое число M 0 , что

f x

M вблизи точки x a .

Теорема 7. Если функция

f x имеет конечный предел при x a , то она ограничена

вблизи точки x a .

Доказательство. Пусть lim f (x) A ,

f (x) A

, тогда

т.е.

x a

f (x)

f (x) A A

f (x) A

A

или

f (x)

A

, т.е.

f (x)

M , где M

A

Теорема доказана.

Некоторые замечательные пределы.

Первый замечательный предел. lim

sin x

1

x 0

x

Доказательство. Рассмотрим тригонометрический круг. Имеем

28

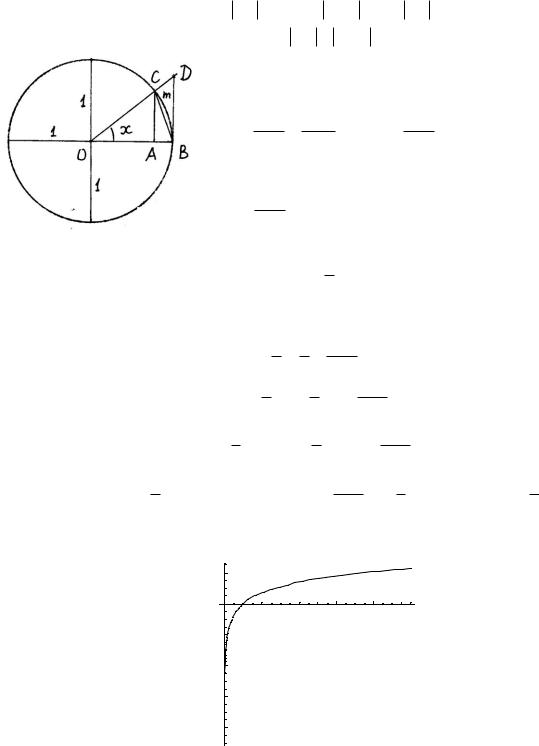
AC sin x,

BmC x,

BD tgx

Так как

AC BmD BD то

sin x x tgx

( при 0 x ).

2

Разделим неравенство на

sin x 0 , тогда

1

x

1

или 1 sin x

cos x

sin x

cos x

x

Применяя теорему о трёх функциях находим, что

lim sin x 1

x 0

x

1 x

e

Второй замечательный предел. lim 1

x

x

Доказательство.

Предположим:

n x n 1

1

1

1

n

x

n 1

1

1 1

1

1

1

n

x

n 1

1

n 1

1

x

1

n

1

1

1

n

x

n

1

1 n 1

e 1 e;

1

n

e

e;

1 x

e

Найдем lim 1

lim 1

n 1

lim 1

n

n

n

1

x

x

Число е является основанием натурального логарифма.

log

e

x ln x y,

т.е.

e y

x.

2

2

4

6

8

10

- 2

- 4

- 6

- 8

Выше представлен график функции y ln x .

Связь натурального и десятичного логарифмов.

	Пусть x 10y , тогда			ln x ln10y , следовательно ln x y ln10
	у = lg x	ln x	M ln x;	ln x	1	lg x , где M	1	0,43429 - модуль перехода.
		ln10			M		ln10

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

29

Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

lim

ln(1 x)

1;

lim

a x 1

ln a;

lim

(1 x)m 1

m.

x

x

x

x 0

x 0

x 0

0,

при

n m

lim

Pn (x)

a0

,

при

n m

b

x Q (x)

m

0

при

n m

,

где P

x a xn a xn 1

a

x a ,

Q

x b xm b xm 1 b

x b - многочлены.

n

0

1

n 1

n

m

0

1

m 1

m

Доказательство последнего предела.

xn (a

a1

...

an

)

a

a1

...

an

P( x)

0

x

xn

xn m

0

x

xn

Q( x)

xm (b

b1

....

bm

)

b

b1

...

bm

xm

0

x

xm

0

x

a0		,	n m
	b
0			n m
,
0,			n m

Бесконечно большие функции и их связь с бесконечно малыми.

Определение. Предел функции f x при x a , где a - число, равен бесконечности,

если для любого числа M 0 существует такое число 0 , что неравенство f x M

выполняется при всех х, удовлетворяющих условию

0 x a

Записывается lim f (x) .

x a

Собственно, если в приведенном выше определении заменить условие f x M на f x M , то получим:

lim f (x) ,

x a

а если заменить на f x M , то:

lim f (x) .

x a

Графически приведенные выше случаи можно проиллюстрировать следующим образом:

Определение. Функция называется бесконечно большой при x a , где a – число

или одна из величин , + или - , если lim f (x) A , где А – число или одна из величин ,

x a

+ или -.

30