
Метод обратных функций
Лемма.
Если
случайная величина
 имеет плотность распределения
имеет плотность распределения
 ,
то случайная величина
,
то случайная величина

 имеет равномерный закон распределения на
интервале
имеет равномерный закон распределения на
интервале  , т.е.
, т.е.

Теорема.
Пусть
 – функция распределения некоторой
случайной величины
– функция распределения некоторой
случайной величины
 ,
γ
– случайная величина с равномерным
законом
распределения на интервале
[0, 1]. Тогда случайная величина
,
γ
– случайная величина с равномерным
законом
распределения на интервале
[0, 1]. Тогда случайная величина
 ,
где
,
где
 –
обратная функция
–
обратная функция ,
подчиняется закону распределения
,
подчиняется закону распределения  .
.










 1
1




Исходя
из этого, случайное число
 ,
подчиняющееся закону
,
подчиняющееся закону
 ,
,
определяют по формуле:

Пример.
Пусть
 .
Пусть получено равномерно распределенное
на
.
Пусть получено равномерно распределенное
на
 случайное
число
случайное
число
 .Решаем
уравнение
.Решаем
уравнение
 (2)
(2)


С учетом этого уравнение (2) принимает вид
 ,
,
откуда
 .
Последнее верно, т. к. и
.
Последнее верно, т. к. и
 ,
и
,
и
 - равномерно распределенные на
- равномерно распределенные на
 случайные числа.
случайные числа.
К
сожалению, интегралы могут быть
«неберущимися», и тогда пришлось бы
использовать численное интегрирование
совместно с численным решением уравнения
(2). Это крайне трудоемкая процедура,
которая приводит к ощутимым затратам
машинного времени.
Вернемся к имитационной модели.
В
нашем случае от подобных процедур легко
избавиться, если учесть, что на практике
функция
 - монотонно возрастающая. Это позволяет
для заданного времени безотказной
работы
- монотонно возрастающая. Это позволяет
для заданного времени безотказной
работы
 найти значения
найти значения
 .
Тогда проверка работоспособности
элементов сведется к проверке условия
.
Тогда проверка работоспособности
элементов сведется к проверке условия
 ,
,
где
 -
равномерно распределенное на
-
равномерно распределенное на
 случайное число;
случайное число;
 -
номер элемента;
-
номер элемента;
 -
номер очередной реализации случайного
процесса.
-
номер очередной реализации случайного
процесса.
Это
равносильно условию
 .
.

Как видно, громоздкая процедура вычисления обратной функции здесь не требуется.
Можно также существенно упростить логическое выражение, если перейти от события «безотказная работа системы» к событию «отказ системы». Отказ системы означает истинность выражения

С учетом сделанных упрощений алгоритм моделирования принимает следующий вид.
-
По заданному времени безотказной работы системы
 вычислить
вычислить
 .
.
-
Положить
 ,
,
 .
. -
Получить три равномерно распределенных на
 случайных числа
случайных числа
 .
. -
Проверить истинность логического выражения
 . Если
оно истинно, то положить
. Если
оно истинно, то положить
 и перейти к шагу 5; иначе перейти к шагу
5.
и перейти к шагу 5; иначе перейти к шагу
5. -
Положить
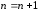 .
. -
Если
 ,
перейти к шагу 3; иначе вычислить и
вывести
,
перейти к шагу 3; иначе вычислить и
вывести
 .
.
-
Стоп.
При построении закона распределения эти действия необходимо повторять последовательно для всех значений t от 0 до arg(P(t)<=0.01), т. е до тех пор, пока вероятность безотказной работы не опустится до значения 0.01 или менее. Среднее время безотказной работы следует вычислить для этого же диапазона значений t.
