fullKG

x	R
n 1
x	cos
n

R cos	n

cos(

xn

n	) R cos		n	cos R sin	n	sin
y	n	sin

R sin	n	x
		n

cos

sin

Постоянные коэффициенты (их постоянно не нужно вычислять).

Т. е. мы затрачиваем на перевод меньше времени (расчет тригонометрических функций задача медленная)

y	n 1	y	n	cos x	n	sin

- Это если центр находится в начале координат.

Если центр не находится в начале координат:

	x x	R cos		(x x ) R cos
	0			0
	y y	R sin		( y y ) R sin
	0			0

(x	n 1	x	) R(cos	n
		0

При описании всех правильных прямых (окружность, дуга окружности, эллипс, дуга эллипса, параболы, гиперболы) стремятся использовать параметрическое задание.

Эллипс:

xn 1 yn 1



a b

cos(		n
sin(	n

b



))

y*

y

x

β

x*

Начинаем формировать с нулевого угла. Для этого считаем сначала точку для обычного эллипса, а потом поворачиваем полученную точку на угол " ".

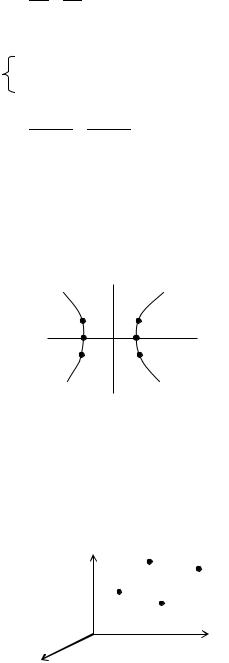
Каноническое описание

y a

	2		x
	2		b

2 2

1

Параметрическое описание гиперболы:

x b sec
y a tg
	sin		2				1
											1
			2					2
	cos					cos
sin		2		1 cos						2	- это тождество.

Для определения энной точки

x	n 1
y	n 1



bsec(
atg(	n

n)

)

Используем формулу разложения sec и tg и получаем зависимость точки от предыдущей.

3	1
4	2

Считаем точку 1, точки 2-3 получаются отображением.

13. Представление пространственных кривых в машинной графике с помощью кубических сплайнов. Задание концевых условий и их влияние на ход кривой.

Неправильные кривые.

Они задаются массивами точек. В параметрическом виде.

y	р1	р3
	р0
		р2

х

z

Методы формирования плавных кривых.

1.Требует прохождения через все заданные точки

2.Определяется этими точками, но через них не проходят

P(t)

- под

P

понимается координата либо “x”, либо “y”, либо “z”

Можно кривую описать полиномом “n+1” степени

P(t) A At A t			2	... A t	n
					n
0	1	2		n

“n+1” неизвестное (коэффициенты А)

у нас есть “n+1” точка, т. е. составляем систему из “n+1” уравнения

при

“n+1” уравнение

t 0	P P(t o) A
	0		0
при t t		P P(t ) A			A t A t 2		... A t n
	1	1	1	0	1	2	n n

………………………………………..

при

	t t		P P(t		) A	A t		A t	2	... A t	n
		n					n		n		n
			n	n	0	1		2		n

Решив эту систему мы получим все неизвестные А, и кривая будет проходить через заданные точки.

Кривая имеет "n"непрерывных производных, эта кривая будет плавная, но волнистая.

Система долго решается Нам нужно, чтобы на внутренних промежутках кривая имела хотя бы один

перегиб, но она может его и не иметь.

Минимально возможная степень кривой – третья

i i 1 : P(t) A At A t			2	A t	3
0	1	2		3

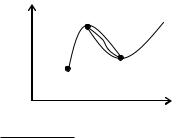
Имеем четыре неизвестных, а промежуток задаем двумя точками, т. е. мы можем написать систему из двух уравнений. Нам не хватает двух условий. Дополнительные условия накладываются на концы кривой и задаются производными.

	'			"		'	P	'	"	"
t 0 P; P		/ P			/ P			1	; P	P	1
i	i			i		i	i		i	i
t 1 P	; P		'	/ P		"
			1			1
i 1		i			i

На первую производную или на вторую производную, либо принимаем за “0” или за “const”, или на равенство производных.

р1

* *

р0 ** **

Производные * и * равны. ** и ** также равны.

Т. е. производные справа и слева от точек равны для плавности.

n + 1 +2 = n + 3

n+1 внутренние уравнения

+2 для границ

n+3 по каждой координате

Кубическая аппроксимация.

0 ≤ t ≤ 1

1

P' (t) A1 2A2t 3A3t2

P A

1 0

P2 A0 A1 A2 A3

	P	'	A
	1		1
	P	'	A 2A 3A
	2		1	2	3
Для Р1	: t = 0
Для Р2	: t = 1

сначала на кривой находятся точки

строится математическое задание

сравнивается с заданной

сдвигаем точки туда, куда надо

пересчитываем точки

Чем больше точек, тем сложнее описание и дольше считать.

14. Параболическая интерполяция пространственных кривых. Ее особенности по сравнению с другими методами представления кривых.

Параболическая аппроксимация

p1

p3

p2

p0

Смешанная С(r) в итоге получили плавную

Предполагает описание тремя параметрами	P	(t)	P	(at	2	bt c)
	1		a

три неизвестных, кривая должна пройти через три заданных точки

Переходя к следующему участку, формируем новую кривую через три следующие

точки: P2 (q) Pb (	2	)

Когда мы стыкуем эти параболы они получаются не гладкие и на участке от

P2 строят смешанную параболу, полученную из смешения этих двух:

C(r) P (t) (1 2) P (q)r
1	2

0 r 1

P1

до

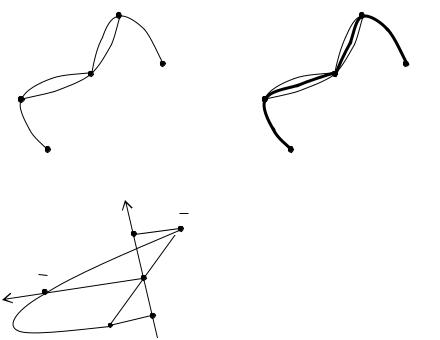
Достоинства: Строим последовательно. Формирование описания проще.

Вточке Р1 – определяется кривой Р1 которая слева.

Вточке Р2 – определяется кривой Р2 которая справа.

Кривые

Кубический сплайн – формируется через три последовательные точки.

Через первые две точки проходит единичная парабола.

Следующие три точки дают смешанную параболу на первых двух точках и мы получаем перегиб и т. д.

Первая производная будет непрерывная, только на самых концах, там где чистые

параболы.	Р3		Р3
Р2	Р4	Р2	Р4
Р1

Р0	Р0
Выбор координатной системы в пространстве:
х*
х*2	Р2

						(		2		0 )
							Р		Р
Р1			Рср
						2
У*
			х*0
	Р0(х0,у0,z0)

Парабола – это плоская кривая.

Парабола меняется от Х*0 до Х*2.

При:

Х=Х0* проходит через точку Р0 Х=0 проходит через точку Р1 -Х0*=Х=Х2* проходит через т Р2

у Р(х) Р (ах	2	вх с)
1

Следует отметить, что будет неоднозначность параболы, если выберем систему координат по-другому.

Достоинство параболической аппроксимации в том, что она позволяет формировать кривую последовательно, т.е. мы можем постепенно ее корректировать и сможем подогнать ее к требуемой кривой не пересчитывая полностью. А при необходимости внутренней корректировки будет достаточным отредактировать только три внутренние точки, в отличии, от кубической аппроксимации, в которой надо было сразу считать все точки и только потом подгонять.

В кубическом сплайне непрерывных две производных. В параболическом – только первая производная непрерывная.

14. Параболическая интерполяция пространственных кривых. Ее особенности по сравнению с другими методами представления кривых.

Параболическая аппроксимация

p1	p3
p2
p0
Смешанная С(r)
в итоге получили плавную
Предполагает описание тремя параметрами		P	(t)	P	(at	2	bt c)
		1		a

три неизвестных, кривая должна пройти через три заданных точки

Переходя к следующему участку, формируем новую кривую через три следующие

точки: P2 (q) Pb (	2	)
Когда мы стыкуем эти параболы они получаются не гладкие и на участке от P1			до
P2 строят смешанную параболу, полученную из смешения этих двух:
C(r) P (t) (1 2) P (q)r
1		2
0 r 1

Достоинства: Строим последовательно. Формирование описания проще.

Вточке Р1 – определяется кривой Р1 которая слева.

Вточке Р2 – определяется кривой Р2 которая справа.

15. Кривые Безье. Их формирование и особенности.

Эти кривые только определяют ход кривой.

Р2

Р1

Р3

Р0 Особенности:

	Р1
Р4
Р5	Р2	Р3

1.Подходит по касательной к внешним ребрам задающего многоугольника, а остальные точки определяют вид кривой. Позволяют качественно оценить ход кривой от задающего многоугольника, задаются параметрически.

2.Это кривая n-ой степени, т.е. сколько ребер – такой степени получается кривая. Можем влиять на степень кривой только изменением количества точек.

	n
Р(t)	i
	P
	i 0

	N		(t)	n!
		i, n		i!(n - i)!

N	i,n	(t)

t	i	(1-

,где Р(t) – полиномиальная функция Рi – вес каждой точки

Ni, n – весовой коэффициент i – номер точки

n – количество точек входящих в определяющий многоугольник.

n-i	, где n! 5* 4*3* 2*1, 0! 1
t)

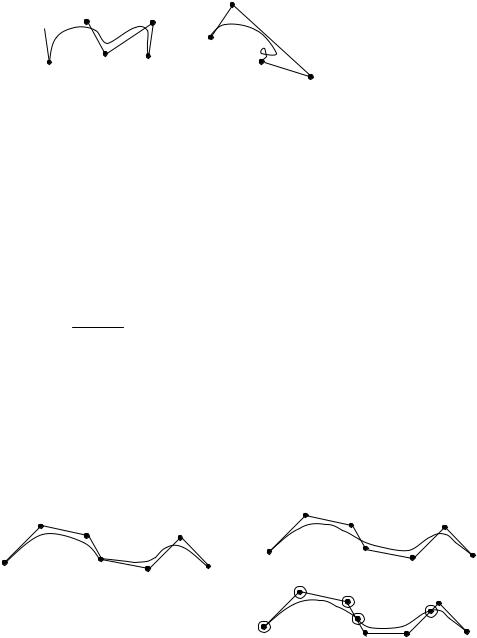
Если множество точек, то строим либо кривую n-ой степени, либо пытаемся построить кривую не высокой степени (например кубическую), но мы находимся в противоречии с количеством точек, тогда мы постепенно будем создавать по четыре точки, но кривая в местах стыка будет неплавная и чтобы этого избежать в последнее ребро вставляем дополнительную точку Р и ее берем за последнею точку данного характеристического многоугольника и первой точкой следующего характеристического многоугольника и тогда она будет плавной кривой третьей степени и называться составной кривой Безье.

Кривая 3 степени:

Составные кривые Безье:

Р

Р

16. Представление кривых с помощью В-сплайнов. Понятие об узловом векторе и его компонентах. Особенности В-сплайнового представления кривых.

Параметрические кривые, у В-сплайновой кривой и кривой Безье общее выражение похоже

	n
Р(t)	P J	i,k	(t)
	i
	i 0

где J – весовой коэффициент, который вычисляется рекуррентно.

1

x

i

t x

i 1

Ji,1

(t)

t

x

t x

0

i

i 1

J

(t)

t - x

i

J

(t)

x

i k

t

J

(t)

i, k 1

i 1,k

x

i,k

x

x

i k-1

i k

i 1

Все коэффициенты вычисляются заранее.

К – это порядок В-сплайна (не степень кривой, а на единицу больше).

Если В-сплайновая кривая четвертого уровня – то это кубическая кривая

Х – элементы углового вектора, который принимает целочисленные значения

{Х0, ….,Хi, ….,Хmax} где Хi Хi+1

xmax=n-k+2, где n – количество сторон, к – порядок Х={0,….,n-к+2}

t – меняется непрерывно от {0 t<tmax=n-k+2}

Число элементов {Х0 ….Хi ….Хmax} в этом узловом векторе связано с числом n и к, т.е. длина узлового вектора L=n+1+k

X {X 0 ,...X i ,...X max }

X i X i 1

В-сплайн характеризуется порядком “К”

1		3	Pi – точки
			(n+1) – точка
			можем построить разные В-сплайновые кривые.
			Порядок их от 2 до (n+1)
0	2		4 2 K n 1

1 степень _ кривой n