978-966-10-2413-6_Matematuka 11_rus

Первообразная				211
	Графиком зависимости высоты h(t) от времени t является часть
параболы, изображенной на рис. 130.
99	Контрольные вопросы
1°.	Может ли функция иметь одну первообразную на некотором
	промежутке?
2°.	Могут ли пересекаться графики первообразных для одной и
	той же функции?
3°.	Среди функций, приведенных ниже, выберите те, которые яв-
	ляются первообразными для одной функции:			г) у = 2х2.
	а) у = х2;	б) у = (х – 1)2;	в) у = х2 + 1;
4°.	Верно ли, что первообразная для произвольной степенной
	функции является степенной функцией?
5.	Пусть у = F1(x) и у = F2(x) – две первообразные для одной фун-
	кции у = f(x). Известно, что		F1(1)= 3, F1(3)= 1,	F2(1) = 5. Чему
	равняется	F2(3)?
6°.	Какой вид имеет первообразная для функции у = sin x, гра-
	фик которой проходит через точку А(0; 0)?
7.	Пусть у = F1(x) и у = F2(x) – две первообразные для одной фун-
	кции у = f(x). Какой вид имеет график функцииу = F2(x) – F1(x)?
8*. На рис. 131 изображен график первообразнойу = F(x) для фун-
	кции у = f(x). Укажите: а) нули функции
	у = f(x); б) промежутки, на которых фун-
	кция у = f(x) принимает положительные
	значения.
9*. Первообразная для функции у = f(x) яв-
	ляется возрастающей функцией. Каким
	свойством обладает функция у = f(x)?

2. Правила нахождения первообразной

Одна из основных задач интегрального исчисле- ния— нахождениедляданнойфункциивсехеепер- вообразных, если они существуют. При нахождении

первообразных пользуются не только табличными формулами, но и некоторыми правилами интегрирования. Эти правила очень напоминают правила дифференцирования (это и не удивительно, ведь операция интегрирования обратна операции дифференци- рования). Известно, что производная суммы дифференцируемых функций равна сумме производных этих функций. Это свойство порождает соответствующее свойство первообразных.

212	Раздел 4. Интеграл и его приложения

Свойство 1. Если y = F(x), y = G(x) — первообраз-

ные для функций у = f(х) иу = g(х) на некотором проме- жутке, то у = F(х) + G(х) является первообразной для функции у = f(х) + g(х) на этом промежутке.

Другими словами, первообразная для суммы двух функций равна сумме первообразных для этих функций.

 Это свойство непосредственно вытекает из определения пер- вообразной и известных правил дифференцирования. Действи- тельно, так как F ′(x) = f(x), G′(x) = g(x), то

( F(x) + G(x))′ = F ′(x) + G′(x) = f(x) + g(x) . g

Свойство 2.Если у = F(х) — первообразная для фун- кции у = f(х) на некотором промежутке и k — постоян- ная, то у = kF(х) является первообразной для функции у = kf(х) на заданном промежутке.

 Действительно, еслиF ′(x) = f(x), то (kF(x))	= kF (x) = kf (x) . g
′	′
Пример 2. Найти первообразные для функции y = 3sin x +		1
на интервале (0; + ∞) .		x

Так как функция y = − cos x — первообразная для функции

у= sin x, то, согласно свойству 2, функция y = −3cos x — первоо-

бразная для		y = 3sin x . Первообразная для функции y = 1 на
промежутке			x
		(0; + ∞) — функция y = ln x, поэтому первообразными
для y = 3sin x +			1 являются функции вида y = −3cos x + ln x + C
(см. свойство 1).			x
			g
Ответ.	y = −3cos x + ln x + C .
Пример	3.	Найти первообразные для функцииf (x) = x2 − 3x + 1 ,

графики которых проходят, соответственно, через точки А(0; –1) и

	1
B 1;	3	. С помощью какого преобразования можно получить гра-
фик второй первообразной из графика первой первообразной?
		Первообразные				для функции у = f(x) имеют вид:
F(x) =		x3	−	3x	2	. Найдем первообразную F1(x), проходящую
		3		2	+ x + C

Первообразная

213

через

точку

А(0;

–1).

Для

нахождения

С имеем

уравнение

−1 =

0

−

0

+ 0 + C , то есть С = –1. Следовательно,

F (x) =

x3

−

3x

2

+

3

2

1

3

2

+

х – 1. Найдем первообразную F2(x), график которой проходит

через

точку

1

Для

нахождения

С имеем

уравнение

B 1;

.

3

− 3x2

+ x + 1 .

1 = 1 − 3 + 1 + C , то есть С = 1 и F (x) = x3

3

3

2

2

2

3

2

2

График функции y = F2 (x)

можно получить из графика фун-

кции

y = F (x) параллельным переносом на 3

единицы в на-

1

2

правлении оси у. g

3x

3x2

1

Ответ.F (x) =

x3

−

2

=

x3

−

+ x +

.

+ x −1 , F (x)

1

3

2

2

3

2

2

Мы знаем, что производная функции

y = f (kx + b)

находится по формуле y (x) = k f (u) , где u = kx +b.

′

′

Используя эту формулу, получим еще одно свойство

первообразной.

Свойство 3. Если у = F(х) — первообразная для фун-

кции у = f(х), то y =

1 F(kx + b) является первообразной

k

для функции у = f(kx + b), где k ≠ 0, b — некоторые по-

стоянные.

 Действительно, если F ′(x) = f(x), то по правилу дифференци-
рования функции у = F(u), где u = kx + b, имеем:
1	′	1	′	=	1	′
	F(kx + b) =	k	(F(kx + b))		k	k F (u) = f(u) = f (kx + b) . g
k
Из этого свойства вытекает правило нахождения первообраз-
ной для функции		y = f (kx + b)		:

1)найти первообразную y = F(x) для функции y = f(x);

2)в выражении для функции y = F(x) аргумент х заменить ли- нейным выражением kx + b;

3)полученное выражение умножить на 1k .

214		Раздел 4. Интеграл и его приложения
	Пример 4.	Найти первообразные для функции y = (3x + 1)7 .

 Будем действовать по приведенной схеме.

1) Для функции y = x7 первообразной является функция

y =

x8

.

8

2) Заменим в выражении для первообразной аргумент х на ли-

нейное выражение (3х + 1): y =

(3x + 1)8 .

8

1

1

8

3) Умножим полученное выражение на 3 :

y =

(3x + 1) .

24

Функция

1

8

является одной из первообразных для

y =

(3x + 1)

24

функции

y = (3x + 1)7 .

По основному

свойству

первообразных,

искомые первообразные имеют вид: y =

1

(3x + 1)

8

+ C . g

24

Ответ.

1

(3x + 1)

8

+ C .

y =

24

1

Пример

5. Найти первообразные для функции y =

.

cos2 (5x − 4)

 Для функции y =

1

первообразной является функция

cos2 x

у = tg x, поэтому, согласно свойству 3 и основному свойству перво-

образных, искомые первообразные для данной функции имеют вид y = 15 tg(5x − 4) + C . g

Ответ. y = 15 tg(5x − 4) + C .

99	Контрольные вопросы
1°.	Известно, что у = F(x) — первообразная для функции у = f(x).
	Укажите первообразные для функции:
				f (x)		x
	а) у = f(x)+ 1; б) у = –f(x);		в) y =		;	г*) y = f .
				2
						2
2°.	Материальная точка движется неравномерно. Ее скорость изме-
	няется по линейному закону. Каков закон движения точки?
3.	Функции у = F(x) и у = G(x) является первообразными соот-
	ветственно для функций	у = f(x) и у = g(x), причем F(1) = 4 и

Первообразная

215

G(1) = –4. Какова первообразная для функции у = f(x)+ g(x),

график которой проходит через точку А(1; 2)?

4*. Материальная точка совершает гармоническое колебание

вдоль прямой со скоростью v = 3sin(2t – 1), где v — скорость,

м/с; t — время, с. Чему равна амплитуда колебания точки?

Задачи

175°. Докажите, что функция

y = F(x) является первообразной

для функции у = f(x) на заданном промежутке, если:

1) F(x)= 9х2

– 2х + 1, f(x)= 2(9х – 1), –∞ < x

< +

∞;

2) F(x) =

1

, f(x) =

1

, 1 < x < + ∞;

1− x

(1 − x)2

3) F(x)= xex, f(x)= (1 + x)ех, –∞ < x < + ∞;

4) F(x) =

1

, f(x) =

sin x

, 0 < x <

π .

cos x

cos2 x

2

176°. Найдите первообразные для функции:

1

1) у = 5;

2) у = х7;

3) у = х–3;

4) у =

;

5) у = 1

7) у = 1

x2

;

6) у = 3 x2 ;

;

8) у = x x ;

x

x

9) у = 3х;

10) у = 3–х;

11) у = ех.

177°. По графику одной из первообразных

y = F(x)

для некоторой функции (рис. 132) восстановите

все множество первообразных для этой фун-

кции.

178. Найдите функцию y = g(x), график которой про-

ходит через точку М, если:

1

π

1°)

′

2°)

′

=

; M

g (x) = 1; M(1; 1) ;

g (x)

cos

2

x

0,

;

1

4

3°)

′

=

; M(9; − 2) ;

4°)

′

= e

x

;

M(ln 3; 0) ;

g (x)

x

g (x)

5)

′

1

; М(–1; 2).

g (x) = x

9°) y = – 4cos x + 5sin x + 0,3; 11) y = sin x2 cos x2 ;

216 Раздел 4. Интеграл и его приложения

179°. Найдите уравнение линии, проходящей через точку А(1; –1),

если угловой коэффициент касательной к ней в точке с аб-

сциссой х равен: 1)

1

; 2)

1 .

x2

x

что ее скорость v

из-

180°. Точка движется вдоль оси абсцисс так,

меняется с течением времени по закону v = t2. Найдите за-

кон движения точки, если:

1) в момент времени t = 0 точка находилась в начале коор-

динат;

2 .

2) в момент времени t = 1 координата точки равнялась −

181.

3

Точка движется вдоль координатной прямой со скоростью

v = sin t, где v — скорость, м/с; t — время, с. Найдите коорди-

нату точки в момент времени t =

π , если в момент времени

2

t = p она находилась в начале координат.

1

182.

График одной из первообразных для функции y =

про-

2

x

3

ходит через точку

А(4; 1), а другой — через точку

B 1;

.

2

График какой из первообразных расположен выше другого?

С помощью какого преобразования можно получить график

первой первообразной из графика второй?

183. Найдите первообразные для функции:

1°)

y = u2

− 3u + 5;

2°)

y =

1

− 2

x ;

x2

2

3)

y = t 3 t +1;

4°)

y = cos x

+

5

;

cos2 x

5

5°)

y =

1

+

2 −1;

6°)

y = ex

+ cos x ;

x2

x

3

2

7°)

y = 4x(x

2

−1);

1

;

8) y = x +

x

10) y = x2 + x − 2 ; x

12) y = 2x(1,5x + 2–x);

Первообразная

217

13*) y = sin

π

14*) y =

2x +1;

6

− 3x ;

1−x

;

16*) y = (5x + 4)6.

15*) y = e 2

184. Найдите первообразную для функции

у = f(x), график кото-

рой проходит через точку М, если:

2

1

3

π

1°) f (x) = 3 x

−

, М(1; –1);

2°) f(x) =

, M −

4

;3 ;

x

2

sin

2

x

3°) f(x) = 2x – 5ex, M(0; 2);

4°) f(x) = 1 – sin x,

π

;

π

;

M

6

6

5°) y = 3x2 − 1

, М(е; е3);

6) f(x) = e2x + ex sin x , M(0; –3);

x

ex

7)f(x) = cos2 x2 −sin2 x2 , M(π; 0).

185.Найдите функцию у = 3f(x)+ 2g(x), график которой проходит через точку А(0; 1), если:

′	1	′	1	′	1	′	1
1) f (x) =	3	, g (x) = −	2 ;	2) f (x) =	3	, g (x) =	2 .
186*. Найдите первообразную для функции у						= 2 – 3	х, наимень-
шее значение которой на промежутке [0;						1] равно 5.

187. Материальная точка движется вдоль координатной прямой

со скоростью v = v(t). Найдите закон ее движения, если:

1°) v = t2

– 3t

+ 2 и в начальный момент времени (t = 0) точка

находилась в начале координат;

2°) v = 1 + 3sin t и в момент времениt =

3π

координата точки

π ;

2

равнялась −

π

2

π

и при t =

координата точки равнялась 2.

3) v = cos

4

− t

4

188. Материаль-

ная точка дви-

жется

вдоль

координатной

прямой со ско-

ростью v = v(t),

график

кото-

рой изображен

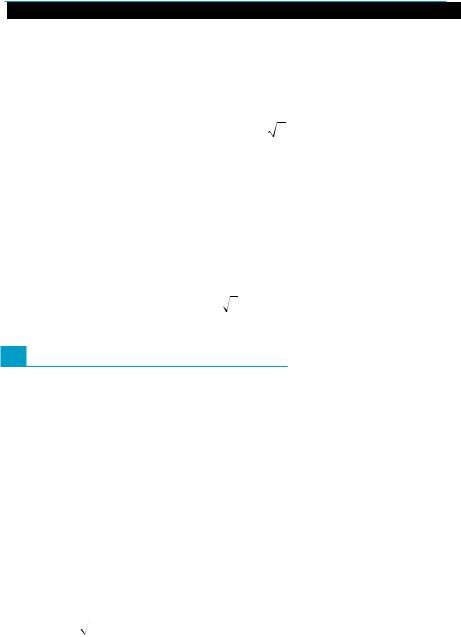
218 Раздел 4. Интеграл и его приложения

на: 1) рис. 133, а); 2) рис. 133, б). Найдите закон движения точки, если в начальный момент времени (t = 0) она имела

координату, равную –1.

	189. Найдите уравнение линии, проходящей через точку А, если
	угловой коэффициент касательной к ней в точке с абсциссой
	х равен:
	1°) 2х −	1 и А(1; 5);				2°) x + ex и А(1; е);
		x
	3) 12 (ex + e−x )			и А(0; 1).
	190*. Материальная точка движется прямолинейно с ускорением
		2t −	π
	a = sin		3	. Найдите:
	а) скорость точки, если ее начальная скорость равнялась
	нулю;
	б) закон движения точки, если в начальный момент време-
	ни она имела координату				3	.
					8

Упражнения для повторения

191. Найдите приращение функции y = f (x) в точке х0, если:

1)f(x)= x2 + 1, x0 = 1, Dx = 2; 2) f(x)= 2x, x0 = 1, Dx = –2.

192.Для функции у = cos x найдите две произвольные перво­ образные и сравните их приращения на промежутке:

1)		π	;	2)		π	;	π	;	3) [x ; x ].
	0;

193.Скорость тела, движущегося вдоль координатной прямой, изменяется по закону v = 2t + 1, где v — скорость, м/с; t — время, с. Найдите ускорение движения тела в момент вре- мени t = 2 с.

194.Изобразите фигуру, ограниченную линиями:

1)у = cos x, − 2π ≤ x ≤ 2π и у = 0;

2)у = 1 – х2 и у = 0;

3)y = x , х = 1, х = 4, у = 0. 1 24 4 2

Первообразная

219

Итог

Основное понятие

Определение Применение

Функция у = F(х) называется Нахождение закона движе- первообразной для функции ния по скорости; скорости — по у=f(х) назаданномпромежутке, ускорению.

если для всех х из этого проме­ жутка выполняется равенство

F ′(х) = f(х).

	Основные утверждения
Название	Формулировка,
утверждения	геометрическая интерпретация
Основное	Если у = F(х) — перво-
свойство	образная для функции
первообразной	у = f(х) на некотором про-
	межутке, то существу-
	ет бесконечное	множе-
	ство первообразных для
	функции у = f(х) на этом
	промежутке и	все они
	имеют вид:
	у = F(х) + С,
	где С — произвольная постоянная.
Правила	1) Первообразная для суммы двух функций
нахождения	равна сумме первообразных для этих функ-
первообразной	ций.	— первообразная для функ-
	2) Если y = F(x)
	ции у = f(х) и k — постоянная, то у = kF(х)
	является первообразной для функцииу = kf(х).
	3) Если y = F(x)	— первообразная для функ-
	ции y = f (x) , то	y = 1 F(kx + b) является пер-
		k
	вообразной для функции y = f (kx + b) , где
	k ¹0, b — некоторые постоянные.

§10. Интеграл

В этом параграфе рассматривается одно из основных понятий математики — интеграл, изучаются его свойства, методы вычисления и некоторые приложения в геометрии и в физике.

1. Физический и геометрический смысл интеграла

Решение многих прикладных задач сводится к на-

хождению приращения первообразной для задан- ной функции на некотором промежутке.

Рассмотрим задачу о нахождении перемещения материальной точки, движущейся прямолинейно со скоростью v = v(t), за проме- жуток времени [t0; T].

Мы знаем, что если x = x(t) — закон движения материальной точки, то есть зависимость ее координаты от времени, то x′(t) = v(t). Это значит, что функция x = x(t) – одна из первообразных для фун- кции v = v(t). Перемещение точки за промежуток времени [t0; T] равно разности ее координат в моменты времени T и t0, то есть x(T) – x(t0). Следовательно, перемещение точки равно прира-

щению первообразной для функции v = v(t) на промежутке

[t0; T].

В частности, если точка в течение промежутка времени [t0; T] движется в одном направлении (направлении оси х), то ее пере- мещение совпадает с путем, пройденным точкой за этот промежу- ток времени. Например, известно, что скорость тела при свобод- ном падении выражается формулой v = gt, где v – скорость, м/с; t — время, с; g ≈ 9,8 м/с2 — ускорение свободного падения. Тогда путь, пройденный телом за первые 4 секунды падения, равен

приращению первообразной F(t) = gt22 для функции v = gt на про-

межутке [0; 4], то есть s = F(4) – F(0)= g 242 – 0 = 8g ≈ 78,4 м.