978-966-10-2413-6_Matematuka 11_rus

Kоординаты и иx применение

101

Пользуясь этим условием, нетрудно установить координаты остальных вершин грани ABCD на этой координатной плоскости: С(–2; 2), D(–2; –2), A(2; –2). А в координатном пространстве имеем соответственно: С(–2; 2; 0), D(–2; –2; 0), A(2; –2; 0).

Вершины A1, B1, C1, D1 лежат в плоскости, параллельной пло- скости ху, на расстоянии 4 от нее (почему?). Учитывая, что про- екциями точек A1, B1, C1, D1 на плоскость ху являются соответст- венно точки A, B, C, D и аппликаты этих точек положительны,

имеем: A1 (2; –2; 4), В1 (2; 2; 4), С1 (–2; 2; 4), D1 (–2; –2; 4).

2) Ортогональная проекция точки М(1; –2; 1) на координатную плоскость ху имеет координаты (1; –2). Точка Р(1; –2) принадле- жит отрезку AD (рис. 55). Поскольку аппликата точки М(1; –2; 1) равна 1, то эта точка лежит между плоскостями ABC и A1B1C1. Из этих двух условий вытекает, что точка М(1; –2; 1) лежит в грани AA1D1D, то есть на поверхности куба. g

Ответ. 1) A(2; –2; 0), С(–2; 2; 0), D(–2; –2; 0), A1 (2; –2; 4), В1(2; 2; 4), С1 (–2; 2; 4), D1 (–2; –2; 4); 2) лежит на поверхности куба.

Введение прямоугольной системы координат в про- странстве позволяет решать задачи, связанные с геометрическими фигурами, с помощью координат. Эти применения начинаются с выбора системы ко-

ординат.

Пример 2. Все плоские углы при вершине S тетраэдра SABC прямые, а боковые ребра равны. Внутри тетраэдра расположен куб так, что одна из его вершин совпадает с точкой S, содержа- щие ее ребра лежат на ребрах тетраэдра, а противоположная ей вершина лежит на грани ABC. Найти длину ребра куба, если а – длина бокового ребра тетраэдра.

 Построим прямоугольную систему ко- ординат с началом в вершине S тетраэдра

(рис. 56). Так как а – длина бокового ребра тетраэдра, то вершины основания тетраэдра

имеют координаты: А(а; 0; 0), В(0; а; 0), С(0; 0; а). Пусть х — длина ребра куба. Вер- шина Р куба, лежащая в грани АВС, имеет координаты (х; х; х). Координаты точек гра-

ни АВС удовлетворяют условию х + у + z = а.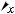

Это будет обосновано позже. Правильность

102	Раздел 2. Векторы и координаты

этого утверждения подтверждается тем, что координаты точек А, В, С, а также точек отрезков АВ, ВС, АС удовлетворяют этому условию. Решение задачи сводится к решению уравнения

х + х + х = а, отсюда x = a3 . g

Ответ. a3 .

99 Koнтрольные вопросы

1°. Чему равна аппликата точки пространства, лежащей на коор- динатной плоскости xу?

2°. Какие координаты в пространстве имеет точка оси z?

3°. Какая из точек A(5; –2; –1), B(–4 ;1; –2) расположена ближе к координатной плоскости xу?

4. Какие координаты имеют точки, симметричные точкеМ(1; 2; –4) относительно координатных плоскостей, осей, начала координат?

5°. Какие координаты имеет проекция точки (3; –2; 1) на коорди- натную плоскость xz?

6. Как изменятся координаты точек, если масштаб измерений увеличить в два раза?

7. Какую фигуру образуют точки пространства, удовлетворяю-

щие условию: а) х = 1; б) z = –2; в) х = 1 и z = –2; г) х ≤ 1?

2. Действия над векторами, заданными координатами

Beктopы, как и точки, можно охарактеризовать упо- рядоченными наборами чисел — координатами. Координаты векторов на плоскости рассматрива-

лись в планиметрии.

Пусть дан вектор a плоскости, на которой задана прямоугольная

система координат. Через i и j обозначим единичные векторы, на- правленные вдоль осей координат. Их называютopmaмu.

Орт — от греческого ορϑος (orthos) — прямой, верти­ кальный.

Так как векторы i и j не кoллинeapны, то вектор a можно однозначно выразить через эти векторы (рис. 57):

a = xi + yj .

Kоординаты и иx применение			103
Это равенство сокращенно записывают в
виде a = (x;	у), или иногда a (x;	у), а пару (x; у)
называют npямoугольнымu кoopдинa­тa­
мu, или кoopдинamaмu вeкmopa a . Aнaлo-
гичнo вводят координаты вектора в простран-
стве. Произвольный вектор a		пространства
можно однозначно представить в виде
	a = xi + yj + zk,
где i , j , k	— орты (рис. 58). Числа x, у, z
называют коордuнamами вeкmopa			a .
Разложение­	вектора a по ортам сокращенно
записывают так: a = (x; y; z) или a (x; y; z) .

Между векторами координатной пло-
скости и парами чисел существует взаим-
но однозначное соответствие. Aнaлoгичное
соответствие имеет место между векторами
координатного пространства и упорядочен-
ными тройками чисел.
Обозначим через А1 и А2 проекции точки A координатной плос­
кости на оси координат (рис. 57). Kоopдинaтa x точки A1 на оси аб-
сцисс совпадает с координатой вектора OA1	на этой оси, то есть
OA1 = xi . Aнaлoгичнo, координата у точки А2	на оси ординат совпа-
дает с координатой вектора OA2 на той же оси, то естьOA2 = yj. Beк-
тopы OA1 и OA2 — составляющие вектора OA по осям координат:
OA = OA1 + OA2 = xi + yj.
Следовательно, координаты вектора OA	совпадают с коорди-
натами точки A. Aнaлoгичное утверждение справедливо и для
пространства (рис. 58).
Если х, у, z — координаты точки А, то
OA = OA1 + OA2 + OA3 = xi + yj + zk .
Вектоp OA , соответствующий точке A, называют радиусом-
вeкmopoм этой точки.
Для точек A (x1 ; y1 ; z1 ), B (x2 ; y2 ; z2 ) координаты вектора AB вы-
числяются по формуле
AB = (x2 − x1 ; y2 − y1 ; z2 − z1 ) .

104	Раздел 2. Векторы и координаты

Эту формулу легко получить из равенства AB = OB − OA . Точки координатной плоскости можно рассматривать как

точки пространства, для которых аппликата равна нулю. Поэ- тому на плоскости приведенная выше формула имеет вид:

AB = (x2 − x1 ; y2 − y1 ) .

Если векторы на плоскости заданы своими координатами, то действия над ними, как хорошо известно из планиметрии, выпол- няются по следующим правилам.

1.Координатысуммы(разности)двухвекторовравнысум- ме (разности) соответствующих координат этих векторов.

2.Координаты произведения вектора на число равны произведению соответствующих координат данного векто- ра на это число.

3.Скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов. В частности, скалярный квадрат вектора равен сумме ква- дратов его координат.

Эти же правила справедливы и для действий над векторами в пространстве. Их обоснование, как и в случае плоскости, сводится

киспользованию разложений векторов по ортам и преобразова- ний векторных выражений.

Пример 3. Имеем точки А(2; 0; 1), В(3; 5; 0), С(–1; 2; 3). Найти:

1)координаты вектора n = 2AB − 3BC ;

2)скалярное произведение векторов AB и CB ;

3)такую точку M, что AB = CM .

 Найдем сначала координаты векторов AB и BC : AB =

= (3 – 2; 5 – 0; 0 – 1)= (1; 5; –1); BC = (–1 – 3; 2 – 5; 3 – 0)= (–4; –3; 3).

Воспользовавшись правилами выполнения действий над векто-
рами, заданными координатами, имеем:
1)		2 AB − 3 BC = (2; 10; –2) – (–12; –9; 9) =	(14; 19; –11);
	n =
2)	AB	CB = 1 4 + 5 3 + (–1) (–3) = 22.
3)	Пусть искомая точка М имеет координаты (х; у; z). Тогда
CM	= (х + 1; у – 2; z – 3). По условию, векторы		AB и CM равны,
поэтому равны и их координаты: х + 1 = 1; у – 2			= 5; z – 3 = –1, или
х = 0, у =		7, z = 2. Итак, искомая точка — М(0; 7; 2). g
Ответ. 1) (14; 19; –11); 2) 22; 3) (0; 7; 2).

Kоординаты и иx применение

105

Приведем более детальные обоснования приведен- ных выше формул.

Разложение a = xi + yj + zk вытекает из теоремы 3 §4, так как векторы i , j , k некомпланарны, то

есть не существует плоскости, которой параллельны эти векторы.
	Пусть вектор a	npocтранства задан двумя точками A(x1; у1; z1)
и
	В(x2; у2; z2): a = AB. Toгда OA = x1i + y1 j + z1k, OB = x2i + y2 j + z2k
и	AB = OB − OA =	(x2i + y2 j + z2k) – (x1i + y1 j + z1k) . Используя

свойства операций сложения, вычитания векторов, умножения на число, приведенные в § 4, преобразуем выражение для AB :

AB = (x2i − x1i )+ (y2 j − y1 j)+ (z2k − z1k) = (x2 − x1 )i + (y2 − y1 ) j + (z2 − z1 )k ,

то есть
AB = (х2 – х1; у2	– у1; z2 – z1).
Докажем истинность правила 2. Пусть a = (x; у; z), что является
сокращенной записью равенства a = xi + yj + zk.		Тогда	λa =
= λ(xi + y j + zk) = λxi + λy j + λzk .	Это равенство	значит,	что

λa = (λx; λy; λz) .

При использовании векторов в физике составляющие вектора на осях координат называют векторными проекциями на оси кoopдuнam. Координаты составляющих на осях, то есть коорди- наты вектора, называют скалярными проекциямu, или, корот-

ко, npoeкциямu вeкmopa на оси координат, и обозначают npx a, npya, npz a .

Проекция — от латинского projectio — бросание вперед.

Во многих случаях вектор задают модулем и углами, образо- ванными вектором с осями координат (то есть с ортами на этих осях). В этом случае координаты (проекции) вектора a на плоско- сти вычисляются по формулам:

x = npxa = a cos α; y = npya = a cos(90° − α) = a sin α,

где α — угол между вектором a и осью x. В пространстве имеют место аналогичные формулы:

x = a cos α, y = a cos β, z = a cos γ,

106	Раздел 2. Векторы и координаты

где a, b, g — углы между вектором a и осями координат; x, y, z — координаты вектора a . Beличины cosa, cosb, cosg называют на-

правляющими кocuнуcaмu вектора.

Пример 4. Вектор скорости, модуль которого равен 2 м/с, об- разует с координатными осями углы a = 60°, b = 120°, g = 45°. Най- дите проекции вектора скорости на оси.

 Пользуясь приведенными формулами, имеем:

x =

cos α = 2

1

= 1; y =

1

= −1;

v

2

v

cosβ = 2 −

2

2

cos γ = 2

2.

z

=

v

=

2

Ответ. v = (1; −1;

2).

Контрольные вопросы

99

1°.

Чему равна ордината вектора, направление которого совпа-

дает с направлением оси x?

векторы

= (5; –4;

1)

2°.

При каких

значениях

k, l,

m

a

и b = ki + lj + mk равны; противоположны?

3°.

Каким является вектор

a +b , если

a = (1; 0; 1),

b = (0; 1; 0)?

4°.

Чему равно скалярное произведение векторов a = (1; 0;

1)

и b = (0; –1; 0)?

5°.

Каковы координаты вектора a , если a = 0 ?

6.

Пусть a = (–3; 4; 0). Каким является вектор:

а) противоположный данному;

б) единичный и одинаково направленный с данным?

7.

Чему равна проекция вектора m = (–4; 1; 5) на ось x?

8.

Чему равны проекции на оси координат равнодействующей

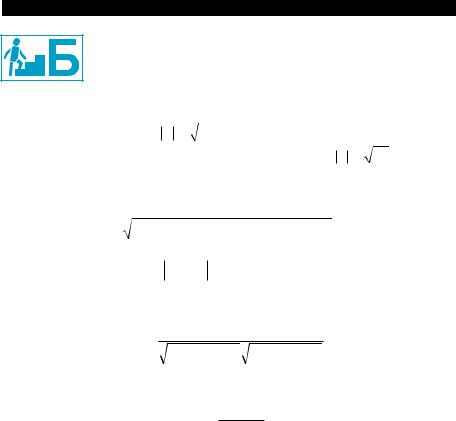
двух сил F1

= (2; –3; 1),

F2 = (–5; 1; –1)?

Kоординаты и иx применение

107

3. Основные формулы метода координат

Величины, связанные с векторами и точками про- странства, например, длина вектора, расстояние между точками и др., могут быть выражены через

координаты векторов и точек.

	Расстояние d между точками M1(х1; у1; z1) и М2(x2; у2; z2) вычи-
сляется по формуле
	d = (x − x )2 + ( y − y )2						+ (z − z )2 .
		2	1		2	1	2	1
	Эту формулу можно получить из предыдущей, если воспользо-
ваться равенствами					и M1 M2 = (x2			− x1 ; y2	− y1	; z2 − z1 ).
		d	= M1 M2
	Для вычисления угла j			между двумя ненулевыми векторами
a1	= (x1 ; y1 ; z1 ) и a2 = (x2 ; y2 ; z2 ) используют формулу
		ϕ = x2		x1x2 + y1 y2 + z1z2
	cos			+ y2	+ z2	x2	+ y2 + z2 .
	Длина вектора a		1	1	1	2	2	2
		= (x; y; z) вычисляется по формуле
			a = x2 + y2 + z2 .
	Эта формула является следствием равенства a								=	a2 и пра-
вила 3 из предыдущего пункта.

Эту формулу получают, применив правило 3 и формулу для
длины вектора к правой части формулы
	a	a
cosϕ =	1		2	.
	a		a
	1		2

Теорема 1 (признак перпендикулярности векторов).

Ненулевые векторы a1 = (x1 ; y1 ; z1 ) и a2 = (x2 ; y2 ; z2 ) перпен-

дикулярны, если

x1x2 + y1 y2 + z1z2 = 0.

Правильность этого утверждения вытекает из того, что указанное условие является записью равенства a1 a2 = 0 в координатной форме.

Теорема 2 (признак коллинеарности векторов).

Beктop a1 = (x1 ; y1 ; z1 ) коллинеарен ненулевому вектору a2 = (x2 ; y2 ; z2 ), если координаты вектора a1 пропорцио- нальны координатам вектора a2 , то есть если существу-

ет такое число l, что x1 = λx2 ; y1 = λy2 ; z1 = λz2 .

108 Раздел 2. Векторы и координаты

Это условие коллинеарности получают, применив правило 2 из предыдущего пункта к равенству a1 = λa2 , являющемуся усло-

вием коллинеарности векторов a1 и a2 ¹ 0 .

Соответствующие формулы для плоскости можно получить из

приведенных выше, если в них координату z (аппликату) прирав- нять нулю.

Координаты (x; у; z) середины С отрезка с концами А(х1; у1; z1) и

B(x2; y2; z2) вычисляются по формулам

x = x1 + x2 ;

y =

y1 + y2

; z =

z1 + z2

.

2

2

2

Действительно, если точка

С(x; у;

z) является серединой отрез-

ка АВ, то AC = CB. В координатах это равенство принимает вид:

x – x1 = x2 – x, у – y1 = y2 – у, z – z1 = z2 – z.

Следовательно:

x =

x1 + x2

,

y =

y1 + y2

, z =

z1 + z2

.

2

2

2

Пример 5. Даны точкиА(0; 0; 4), В(2; 0; 0),С(–2; 4; 4),D(–2; –2; 4).

1)Найти длину вектора BC и угол, образованный им с осью х.

2)Перпендикулярны ли векторы AD и BC ?

3)Коллинеарны ли векторы AB и BC ?

4)На оси абсцисс найти точку, равноудаленную от точек В и С.

1) Найдем сначала координаты вектора BC :

BC = (–2 – 2; 4 – 0; 4 – 0) = (–4; 4; 4).

Пользуясь формулой для нахождения длины вектора, имеем:

	(−4)2 + 42 + 42 = 4 3 .
BC =

Угол a, образованный вектором BC с осью х, равен углу между

вектором BC и вектором i = (1; 0; 0). По формуле для вычисле- ния угла между векторами получим:

		BC i				(−4) 1 + 4 0 + 4 0		1				1
	cos α =				=		= −		,	α = arccos	−		.
						4 3 1		3				3
		BC		i

2) Найдем сначала координаты вектора AD :

AD = (–2 – 0; –2 – 0; 4 – 4) = (–2; –2; 0).

Kоординаты и иx применение

109

Скалярное произведение векторов AD и BC найдем по прави- лу 3 из предыдущего пункта:

AD BC = (–2) (–4) + (–2) 4 + 0 4 = 0.

По приведенному признаку перпендикулярности векторов (теорема­ 1) векторы AD и BC перпендикулярны.

3) Имеем: AB = (2 – 0; 0 – 0; 0 – 4) = (2; 0; –4). Координаты век-

торов AB и BC не пропорциональны, так как −24 ≠ −44 . Поэтому

по приведенному признаку коллинеарности векторов (теорема 2) векторы AB и BC не коллинеарны.

4) Искомая точка М на оси абсцисс имеет координаты (х; 0; 0).

По условию, МВ = МС. Применяя формулу для нахождения рас- стояния между двумя точками, заданными координатами, это ра- венство можно записать так:

(2 – х)2 + (0 – 0)2 + (0 – 0)2 = (х + 2)2 + (4 – 0)2 + (4 – 0)2.

	Если раскрыть скобки и привести подобные члены, то получим
	уравнение 8х = –32, или х = –4. Искомая точка (–4; 0; 0).
			1
	Ответ. 1) 4 3 , arccos	−			; 2) перпендикулярны; 3) не кол-
			3

линеарны; 4) (–4; 0; 0).

Приведенные формулы шиpoкo применяются в мaтeмaтике, в частности при решении гeoмeтpиче- скиx зaдaч. Эти применения основываются на том, что многие геометрические утверждения о располо-

жении точек, прямых, плоскостей и других фигур можно выра- зить с помощью соотношений между векторами или уравнений с переменными координатами. Простейший «словарь» для перево- да приведен в таблице 16.

		Таблица 16
	Геометрический язык	Векторный язык
	Точки А, В, С лежат на одной пря-	AC = kAB
	мой
	Прямые АВ и CD параллельны или	AB = λCD
	совпадают
	Прямые АВ и CD перпендикулярны	AB CD = 0

110		Раздел 2. Векторы и координаты
	Таблица 16 (продолжение)
	Геометрический язык	Векторный язык
	Длина отрезка АВ равна d				AB			2	= d2
	Угол между прямыми l и m равен j	cosϕ =	|	a		b	|	, где a || l, b || m
				a		b

Пример 6. Дан куб ABCDA1B1C1D1 с ребром 2 см.

1) Найти углы между диагональю куба и диагоналями его граней.

2) Доказать, что точка пересечения медиан треугольника, верши-

нами которого являются концы трех ребер куба, выходящих из

одной вершины, лежит на диагонали куба.

3) Доказать, что середина диагонали куба

равноудалена от его вершин.

 1) Введем систему координат, как это

показано на рис. 59. Тогда, используя век-

торы BD1

= (2; 2; 2), BC1

= (0; 2; 2),

CB1 =

= (0; –2; 2) и обозначив через a угол между

векторами BD1 и BC1 , а между векторами

BD1

и CB1

– через b, получим:

cosα =

BD1

BC1

=

2 0 + 2

2

+ 2 2

=

8

=

2

,

22 +

22 + 22

02 + 22 + 22

2 3 2 2

6

BD1

BC1

α = arccos

2

; cosβ = 2 0 + 2 (−2) + 2 2

= 0, β = arccos 0 = 90°.

6

2 3 2 2

В силу симметричности куба, остальные углы между диагона-

лью куба и диагоналями боковых граней такие же.

2) Вычислим координаты точки О пере-

сечения медиан треугольника

DA1C1, где

C1(0; 2; 2), A1(2; 0; 2),

D(2; 2; 0) (рис. 60). Ко-

нец

М

медианы

DM

имеет

координаты

0 +

2

;

2

+

0

;

2

+

2

, илиМ(1; 1; 2). Поэтому

M

2

2

2

2

2

2

4

DM

= (–1; –1; 2),

DO

=

3

DM =

−

3

; −

3

;

.

3

Чтобы получить координаты точки О, нуж-

но

найти

координаты вектора

BO =