Сплайновые кривые Безье.

Сплайновая кривая Безье (Bezierspline), в отличие от кривой Эрмита, определяется только заданием опорных векторов. Если заданыN+1 опорные векторы, то кривая Безье порядкаN, строится с помощью следующей формулы:

. (27)

Здесь b_N,i(t)– многочлены Бернштейна, которые обладают следующим свойством:

. (28)

Это, в свою очередь, приводит к тому, что кривая Безье порядка Nобладает следующими свойствами.

1) Кривая Безье – гладкая кривая.

2) Кривая Безье начинается в точке V₀, а заканчивается в точкеV_N.

(29)

3) Кривая Безье в начале при t=0 касается отрезка, а в конце приt=1 кривая Безье касается отрезка. Другими словами касательные вектора в начале и конце кривой Безье параллельны указанным отрезкам.

4) Кривая Безье лежит целиком в выпуклой оболочке порожденной опорными точками . Другими словами, если на этих опорных точках построить выпуклый многогранник, то кривая Безье будет целиком располагаться внутри этого многогранника.

В дальнейшем многочлены Бернштейна b_N,i(t) будем называть функциями Безье. Запишем в явном виде кубическую сплайновую кривую Безье. В этом случае четыре функции Безье будут иметь следующий вид.

(30)

Соответственно кубическая кривая Безье будет вычисляться по следующей формуле.

(31)

Уравнение (21) для кривой Безье можно записать в матричном виде, как и уравнение (25) для кривой Эрмита. Введем столбец, элементами которого будут опорные векторы.

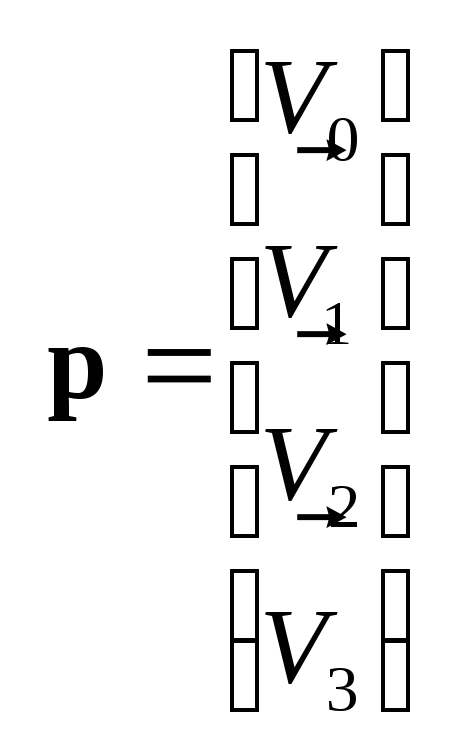(32)

Тогда уравнение кривой Безье (31) можно представить в виде матричного уравнения.

(33)

Здесь матрица M_bназывается матрицей Безье (Beziermatrix) и имеет следующий вид:

(34)

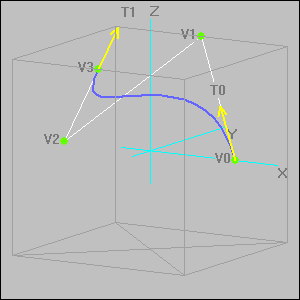
На Рис.13. показана элементарная кривая Безье, построенная с помощью формулы (31). На этом рисунке показаны четыре опорные точки V₀,V₁,V₂,V₃. Из рисунка видно, что кривая Безье начинается в опорной точкеV₀, а заканчивается в опорной точкеV₃.

На Рис.13 показаны также касательные векторы в начале кривой T₀, и в конце кривойT₁. Из рисунка видно, что касательный векторT₀в начале кривой приt=0 параллелен отрезку, а в конце кривой касательный векторT₁приt=1 параллелен отрезку.

Составная сплайновая кривая Безье может быть создана из нескольких стыкующихся между собой элементарных кривых Безье. По сути дела, составная кубическая кривая Безье представляет собой объединение Nэлементарных кубических кривых Безьеc₀,c₀,c₁,,c_N-1. Для определения составной кривой понадобитсяNp= 3N+1 опорных векторов.

Каждая элементарная кривая Безье c_nописывается параметрическим векторным уравнением:

(35)

Здесь векторная функция определятся по формуле (31), где в качестве четырех опорных векторов выступают четыре следующих опорных вектора.

(36)

В опорных точках стыкуются соседние элементарные кривые Безье. Так в точкестыкуются соседние элементарные кривыеc_n-1иc_n, причем выполняется следующее условие:

(37)

На Рис.14. показана составная кривая Безье, полученная путем стыковки трех элементарных кривых Безье.

Рис.13. Элементарная кривая Безье. Опорные точки V0,V1V2,V3. Касательные векторыT0,T1.

Рис.14. Составная кривая Безье. Опорные точки V0,V1,V2,,V9. Касательные векторы – желтый цвет, векторы кривизны – красный цвет.

(Изображение на Рис.13 создано программой line7.cpp, на Рис.14 создано line8.cpp.)

На Рис.14 показаны 10 опорных точек, обозначенные зелеными кружками. Желтыми стрелками показаны касательные векторы в начале и конце каждой элементарной кривой Безье. Красными стрелками показаны векторы кривизны в начале и конце элементарных кривых Безье.

Бросается в глаза, что в местах стыковки составная кривая Безье не является гладкой кривой. Касательные векторы и векторы кривизны в месте стыковки соседних элементарных кривых Безье, вообще говоря, не совпадают.

Чтобы сделать составную кривую Безье гладкой кривой, необходимо предпринять дополнительные усилия по выбору опорных векторов. Пусть стыковка соседних элементарных кривых Безье происходит в точке V_n. Тогда для непрерывности касательного вектора в точке стыковки три вектораV_n-1V_n,V_n+1должны лежать на одной прямой. Такую кривую называютG¹– непрерывной кривой.

На Рис.15. показана гладкая составная кривая Безье, полученная путем стыковки двух элементарных кривых Безье в точке V₃.

Рис.15. Составная кривая Безье. Непрерывный касательный вектор. Опорные точки V2,V3,V4лежат на одной прямой.

Рис.16. Составная кривая Безье. Непрерывный касательный вектор и непрерывный вектор кривизны. Опорные точки V1,V2,V3,V4,V5лежат в одной плоскости.

(Изображения на Рис. 15, 16 созданы программой line8.cpp.)

На Рис.15 видно, что три опорные точки V₂V₃,V₄лежат на одной прямой. В результате касательный вектор оказался непрерывным в точке стыковкиV₃.

Однако в точке стыковки соседних элементарных кривых Безье вектор кривизны претерпевает разрыв. Можно путем выбора опорных точек сделать вектор кривизны непрерывным в точке стыковки. Такую кривую называют G²– непрерывной кривой. Так вот чтобы составная кривая Безье былаG²– непрерывной кривой, нужно чтобы три точкиV_n-1V_n,V_n+1лежали на одной прямой, а пять точекV_n-2,V_n-1,V_n,V_n+1,V_n+2 лежали в одной плоскости.

На Рис.16. показана гладкая составная кривая Безье, которая является G¹– непрерывной кривой иG²– непрерывной кривой. Здесь стыковка соседних элементарных кривых Безье происходит в точкеV₃. Три опорные точкиV₂V₃,V₄лежат на одной прямой, что приводит к непрерывности касательного вектора. В дополнении к этому пять опорных точекV₁,V₂,V₃,V₄,V₅лежат в одной плоскости, что приводит к непрерывности вектора кривизны.