Popov_vorobev

Image1.Canvas.FillRect(Canvas.ClipRect);

Image1.canvas.Brush.Color:=RGB(255,255,255);

Image1.Canvas.Rectangle(0,0,Image1.Width,Image1.Height);

Данные действия необходимо выполнить два раза: при создании формы, когда мы задаем начальные значения угла и цвета прямоугольника, и при изменении пользователем значения угла. Например, в обработчике события TrackBarChange компонена типа TTrackBar. Но только, если в первом случае все параметры у нас фиксированные, то во втором они соответствуют введенным пользователем значениям. Выше приводился пример поиска косинуса угла между нормалью и направлением луча. Это действие как раз необходимо выполнять, например, в обработчике события TrackBarChange или другого, в зависимости от того, как реализовано приложение, и с помощью какого компонента пользователь вводит значение угла. Данное значение в предыдущем примере, мы сохранили в переменной cosNR типа real. Теперь, зная это значение, можно найти цвет области, соответствующий введенному углу и закрасить им область.

color:=255*cosNorm;	//color — вещественная перемен-
	ная, в которой хранится значение
	цвета для каждой составляющей мо-
	дели RGB

Image1.Canvas.FillRect(Canvas.ClipRect);

Image1.canvas.Brush.Color:=RGB(Round(color),Round(color), Round(color)); //так как метод RGB принимает целочисленные значения, переменную color необходимо округлить с помощью встроенной функции Round Image1.Canvas.Rectangle(0,0,image1.Width,image1.Height);

Итак, в практической части выше были описаны основные трудности, с которыми может столкнуться студент, при выполнении данной лабораторной работы. Далее приводятся скриншоты готового приложения (рис. 1–3).

10

Рис. 1. Окно приложения при значении угла 0°

Рис. 2. Окно приложения при значении угла 37°

11

Рис. 3. Окно приложения при значении угла 111°

12

Лабораторная работа № 2

Алгоритм удаления невидимых поверхностей, использующий z-буфер

Теоретическая часть

В первой лабораторной работе кратко говорилось о задаче удаления невидимых поверхностей и, в частности, упоминался метод z-буфера, как один из наиболее простых. В данной лабораторной работе алгоритм z-буфера рассмотрен более подробно, а студентам будет предложено разработать графическое приложение, использующее этот алгоритм.

Предложен данный алгоритм был в 1974 году Эдом Кэтмулом для решения задачи определения видимости объекта в 3D-графике. Другими словами, алгоритм позволяет определить, как объекты перекрывают друг друга. Данная задача решается, в частности, в процессе рендеринга (визуализации) компьютерной 3D-модели, когда на основе формального описания модели, надо получить итоговое изображение, которое увидит пользователь.

При формировании итогового изображения, которое затем выводится на экран, используется два буфера: z-буфер и буфер кадра. В буфере кадра хранятся значения цветов пикселей. Z-буфер используется для запоминания координаты z каждого пикселя. Данный буфер представляет собой двумерный массив, элементы которого соответствуют пикселям экрана. Таким образом, работу алгоритма кратко можно описать так: пиксели объектов просматриваются поочередно, если координата z текущего пикселя больше значения, соответствующего данному пикселю в z-буфере, то это значение заменяется на текущее, а в буфер кадра заносится новый цвет. В противном случае, никакие действия не производятся.

К основным преимуществам алгоритма можно отнести то, что он прост в реализации, решает задачу об удалении невидимых поверхностей и значительно упрощает визуализацию пересечений

13

сложных поверхностей. Кроме того, вычислительная трудоемкость алгоритма увеличивается линейно, а объекты на сцене не нужно сортировать по глубине, то есть их можно заносить в буфер кадра и z-буфер в произвольном порядке, что экономит вычислительное время. Основной недостаток — это большой объем требуемой памяти. Так как информация о глубине должна обрабатываться с достаточной точностью, то под каждый пиксель в z-буфере приходится выделять около 20 бит. Кроме того, к недостатками данного алгоритма принято относить трудоемкость устранения лестничного эффекта и реализацию эффекта прозрачности и просвечивания.

Вернемся к самому алгоритму. Пусть у нас имеется некоторая графическая сцена, на которой расположены трехмерные объекты разной формы, и нам необходимо получить на ее основе двумерное растровое изображение, вид спереди. В данном случае алгоритм начнет работу с того, что заполнит буфер кадра фоновым значением цвета, а z-буфер минимальным значением z, соответствующим также фону изображения. Затем будет произведено преобразование многоугольников в растровую форму. Для каждого пикселя многоугольника будет вычислено значение координаты z, то есть его глубина. После чего, как уже писалось выше, поочередно будет сравниваться глубина каждого пикселя многоугольников со значением, которое уже записано в z-буфер в этой позиции. И, при необходимости, значение в z-буфере и в буфере кадра будет изменяться.

Теперь на примере рассмотрим вопрос получения координаты z произвольного пикселя некоторого многоугольника. Допустим, у нас имеются координаты его вершин. Соответственно, для того чтобы иметь возможность получить координату z любого его пикселя, необходимо найти уравнение плоскости многоугольника.

Итак, пусть координаты вершин многоугольника:

M1 = ( 1 , 2 , –2 );

M2 = ( 3 , 7 , 2 );

M3 = ( –2 , –1 , 1 ).

М ( x ,y ,z ) — произвольная точка, принадлежащая плоскости. Найдем координаты векторов, исходящих из точки M3, соот-

ветственно, в точки M1, M2, M:

14

uuuuur

М3М = (x – (–2 ) , y – (–1 ) , z – 1); uuuuuur

М3М1 = (1 – (–2 ) , 2 – (–1 ) , –2 – 1) = ( 3 , 3 , –3); uuuuuur

М3М2 = (3 – (–2 ) , 7 – (–1 ) , 2 – 1) = ( 5 , 8 , 1).

Таким образом, у нас имеется три вектора, исходящих из одной точки, которые представляют собой некоторую пирамиду. Если все четыре точки лежат в одной плоскости, то объем данной пирамиды равен нулю. Соответственно, именно этот случай нас и интересует. Представить равенство объема данной пирамиды нулю можно следующим образом:

	x −(−2) y −(−1) z −1
	3			3									−3					= 0.
	5			8									1
Данный определитель можно представить в виде разности двух
определителей:
	x −(−2) y −(−1) z −1																						x y						z				−2 −1 1
	3			3									−3						=				3 3 −3								−		3 3 −3
	5			8									1										5	8					1				5		8		1
Первый определитель разлагаем по первой строке:
1+1				x		3 −3						1+2		y							3 −3								1+3				z		3 3					−2 −1 1
(−1)						8 1				+(−1)											5 1						+(−1)								5 8			−		3			3 −3			=
																												−2	−1						1					5			8	1
= x			3 −3					− y		3 −3			+ z					3 3
																								−				3 3 −3								=
			8	1						5	1							5				8						5	8						1

x det A − y det B + z det C −det D;

det A 83 −13 =3 1−(−3)8 =3 −(−24) = 27; det B 53 −13 =3 1−(−3)5 =3 −(−15) =18;

15

det C	3	3	=3 8 −3 5 = 24 −15) =9.
	5	8

Сейчас мы легко нашли определители матриц A, B и C, каждая из которых состоит из двух строк и двух столбцов. Определитель матрицы D(3×3) найти несколько сложнее.

Чтобы упростить эту задачу, прибавим к элементам второй строки соответствующие элементы первой, умноженные на три. Мы можем это сделать, в соответствии со свойством определителя, которое гласит, что если из элементов любой строки (столбца) вычесть или прибавить соответствующие элементы другой строки (столбца), умноженные на произвольное число, то определитель не

изменится. В результате этого получим:
det D =		−2	−1	1				−2	−1	1
		3	3	−3		=		−3	0	0
		5	8	1				5	8	1

Далее разложим определитель по элементам второй строки:
det D = (−1)2+1(−3)		−1	1		+(−1)2+2 0		−2	1		+(−1)2+3 0		−2	−1		=
		8	1				5	1				5	8

=3 −81 11 =3((−1)1−1 8)= −27.

Теперь все четыре значения определителей можно подставить в указанное выше уравнение. Оно и будет являться уравнением плоскости, проходящей через точки M1, M2, M3:

27x – 18y + 9z + 27 = 0.

Сократим уравнение на 9 и получим в итоге

3x – 2y + z + 3 = 0.

Практическая часть

Итак, студентам предлагается реализовать программу, моделирующую процесс работы алгоритма z-буфера. В самом простом виде это должно быть приложение, содержащее некоторое графическое поле, поля для ввода данных о прорисовываемых объектах и кнопку запуска моделирования работы алгоритма. Далее будет

16

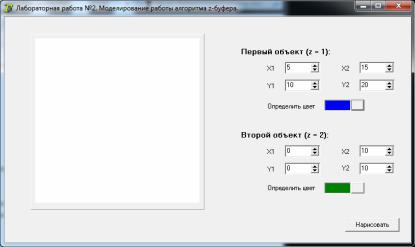
описан принцип работы приложения, удовлетворяющего минимальным требованиям данного задания.

В окне приложения имеются поля для ввода данных о двух объектах, которые будут прорисовываться в графическом поле. Пользователь в них указывает только координаты x и y левой верхней и правой нижней вершин двух прямоугольников, которые будут выводиться на экран, и их цвета. Координаты эти необходимо ограничить значениями, например, от 0 до 25 (рис. 4).

Рис. 4. Ввод входных данных

Это необходимо потому, что в данном случае будет производиться моделирование процесса работы алгоритма с замедлением его по времени. Пользователь будет видеть, как прорисовываются пиксели фона и пиксели графических объектов. Каждый шаг работы алгоритма должен будет производиться с временной задержкой. Поэтому, даже если задержка эта будет минимальной, а размер графического поля всего 250×250, то весь процесс будет занимать достаточно большое время. Таким образом, формальные «точки», из которых будут строиться графические объекты, будут размером, например, 12×12 фактических пикселей. Когда коорди-

17

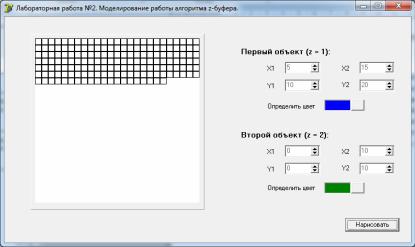
наты и цвет заданы, пользователь нажимает кнопку, запускающую процесс моделирования. В графическом поле начинают последовательно прорисовываться модели «пикселей» фона изображения (рис. 5), а в z-буфер заноситься минимальные значения z.

Рис. 5. Прорисовка моделей пикселей

Далее таким же образом, как фоновые «пиксели» начинают прорисовываться «пиксели» графических объектов, при этом происходит изменение значений в z-буфере (рис. 6–7).

Что касается программной реализации, то все необходимые базовые моменты, касающиеся работы с компонентом TImage, были рассмотрены в первой лабораторной работе. В данной работе рассмотрен только принцип работы с компонентом TTimer, необходимым для реализации временной задержки процесса моделирования. Компонент TTimer находится во вкладке System. Данный компонент не визуальный. Его можно расположить в произвольном месте формы. Работа с ним осуществляется посредством двух основных свойств: Interval и Enabled. Использовать их можно двумя способами. Задать изначально положительное значение свойства Interval, а затем только присваивать значение true свойству

18

Рис. 6. Построение первой фигуры

Рис. 7. Построение второй фигуры

Enabled для запуска таймера и false для остановки. Второй способ — присвоить свойству Enabled значение true, и менять только

19