Popov_vorobev

Рис. 15. Сообщение о результатах отсечения

30

Лабораторная работа № 4

Отсечение многоугольников. Реализация алгоритма Сазерленда-Ходжмена

Теоретическая часть

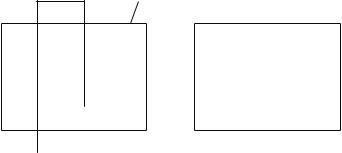
Следующая задача, которая будет рассматриваться в данном методическом пособии — это отсечение многоугольников. Она уже на порядок сложнее задачи отсечения отрезков. На первый взгляд, кажется, что её можно свести к задаче отсечения отрезков, ведь любой многоугольник состоит из ребер, которые представляют собой именно отрезки. Но если это сделать, то получаемая фигура будет не замкнутой. При отсечении многоугольника, в список ребер обязательно придется вносить фрагменты сторон отсекающего многоугольника (рис. 16). Определение этих фрагментов как раз и усложняет задачу.

A	B	Отсекающее окно

a b

		C	D			C	D
				f			e
F			E

Рис. 16. Отсечение многоугольника

Трудности возникают, в частности, когда в результате отсечения получается несколько несвязанных между собой многоуголь-

31

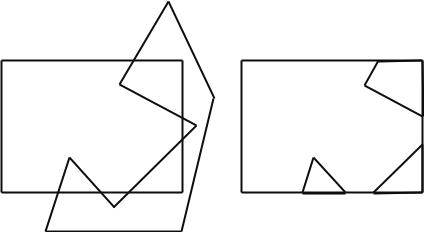
ников меньших размеров (рис. 17). Например, нужно учитывать, что отрезки, соединяющие два многоугольника не должны в итоге входить в список ребер.

Рис. 17. Отсечение многоугольника

Так же как и в случае с отсечением отрезков, задача отсечения многоугольников имеет целый ряд решений, каждое из которых обладает своими достоинствами и недостатками. В данной лабораторной работе мы рассмотрим алгоритм Сазерленда-Ходжмена. Это алгоритм последовательного отсечения многоугольника.

В основе данного алгоритма лежит идея о том, что отсечь многоугольник относительно одной прямой довольно просто. Отсечение в нем происходит в несколько итераций (в зависимости от количества ребер отсекающего многоугольника). Исходный многоугольник отсекается относительно одной стороны окна, затем многоугольник, который получается в результате, также отсекается, только уже относительно следующей стороны и т. д. Этот процесс для прямоугольного окна изображен на рис. 18.

Вначале работы алгоритма одна точка определяется начальной. Далее необходимо рассмотреть все точки из списка вершин многоугольника, кроме первой. Причем рассматривать каждую из них

32

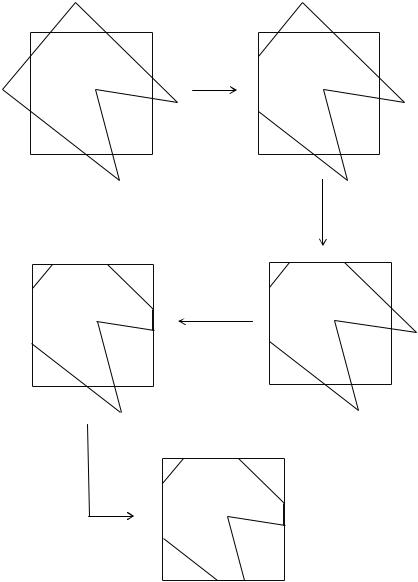
Рис. 18. Порядок отсечения многоугольника

33

мы будем как конечную точку ребра, начальной точкой которого будет вершина, предшествующая ей в списке.

Сопоставляя таким образом каждое ребро многоугольника с отсекающей плоскостью, в список вершин результирующего усеченного многоугольника мы занесем ноль, одну или две вершины.

Если у рассматриваемого ребра начальная и конечная вершины находятся за границей видимой области, то в результат не заносится ни одна точка.

Если обе точки находятся внутри видимой области, то заносится только конечная точка. Начальную точку нет смысла заносить в список, так как в предыдущей итерации она была конечной точкой другого ребра и в результат уже попала.

Если начальная точка находится внутри области, а конечная снаружи, то получается, что ребро «выходит» из области и в результат нужно занести только точку пересечения ребра с отсекающей прямой.

Последний случай — когда начальная точка находится снаружи, а конечная — внутри области, то есть ребро «входит» в область. Тогда в результат надо внести две точки: точку пересечения ребра с отсекающей прямой и конечную точку.

Все эти принципы проиллюстрированы на рис. 19, где S– начальная точка отрезка, P — конечная. Отсечение осуществляется относительно левой стороны прямоугольной отсекающей области.

Особое внимание нужно обратить на последнее ребро. Для работы с ним необходимо запомнить первую вершину многоугольника.

Для определения положения точки отрезка относительно отсекающей прямой и последующего отсечения в случае с прямоугольным окном можно воспользоваться теми принципами, которые были описаны в первой лабораторной работе. Сам же алгоритм Сазерленда-Ходжмена предназначен для отсечения произвольной фигуры любым выпуклым окном. В случае отсечения произвольным выпуклым окном необходимо использовать уже параметрическое представление прямой. Этот метод отсечения используется также в алгоритме Кируса-Бека — алгоритме отсечения отрезка. В рамках данного курса алгоритм Кируса-Бека также

34

P	P

S

S

а)

б)

P

P

S

S

в)

г)

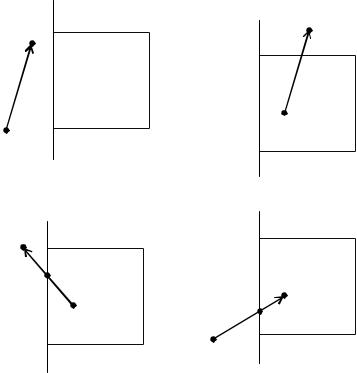
Рис. 19. Положение вершины многоугольника: а — обе точки вне области видимости. В результат не вносится ничего; б — обе точки находятся внутри области видимости. В результат вносится только конечная точка P;

в— начальная точка находится внутри области видимости. Конечная — снаружи.

Врезультат вносится точка пересечения; г — конечная точка находится внутри

области видимости. Начальная — снаружи. В результат вносится точка пересечения и конечная точка. S — начальная точка; P — конечная точка

изучается. Однако в этой лабораторной работе от студента требуется реализовать алгоритм Сазерленда-Ходжмена только для прямоугольной отсекающей области.

Итак, подведем итог теоретической части.

У данного алгоритма имеются следующие недостатки:

35

1)он применим только к выпуклому окну;

2)если в результате отсечения получается несколько изолированных многоугольников, то этот результат также будет включать отрезки, связывающие эти многоугольники.

К преимуществам можно отнести относительную простоту реализации.

Практическая часть

Что касается практической части, то тут, в случае с прямоугольным окном, никаких трудностей возникнуть не должно. Все основные моменты были описаны в предыдущей работе.

Требования к программе

1.Пользователь должен иметь возможность нарисовать произвольный многоугольник, однако стороны этого многоугольника пересекаться между собой не должны. Корректная реализация этого ограничения является одной из сложностей данной лабораторной работы.

Пользователь по нажатию кнопкой мыши в рабочей области добавляет новую вершину многоугольника. Эта вершина сразу же соединяется линиями с предыдущей и первой точками (если точек уже больше двух). Таким образом получается замкнутая фигура. Но прежде чем соединять вершины, программа должна проверить, не получается ли пересечений ребер. И если пересечения получаются, то можно ли от них избавиться путем добавления новых вершин. Если избавиться от этих пересечений невозможно, программа не должна добавлять такую вершину в список, если избавиться всё-таки возможно, то программа должна вершину добавить, но при этом весь многоугольник окрасить в красный цвет и заблокировать возможность перехода к следующему шагу работы до тех пор, пока пользователь не избавится от пересечений. Переход к следующему шагу должен быть возможен только тогда, когда будет нарисован подходящий многоугольник (рис. 20–22).

2.Должны быть реализованы возможности возврата на шаг назад (удаления предыдущей вершины) и полной очистки экрана.

36

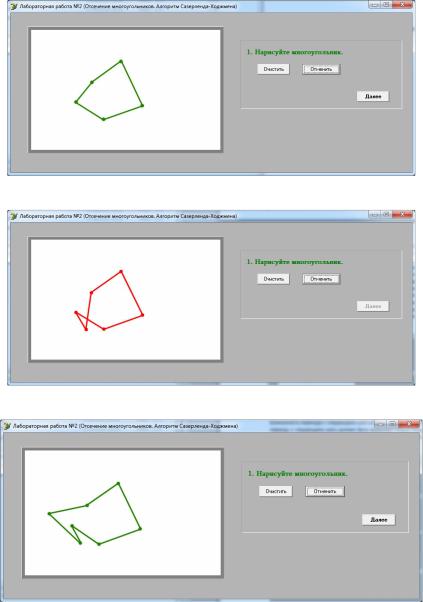
Рис. 20. Рисование отсекаемого многоугольника

Рис. 21. Многоугольник с пересекающимися сторонами

Рис. 22. Невыпуклый многоугольник

37

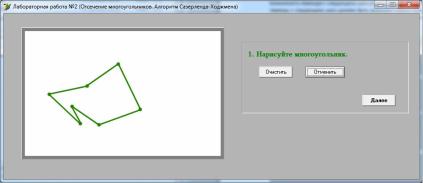
3. Результат отсечения должен выделяться зеленым цветом

(рис. 23).

Рис. 23. Результат отсечения многоугольника

38

Лабораторная работа № 5

Построение графиков функции и кривых высших порядков

Теоретическая часть

В большинстве прикладных задач возникает необходимость прорисовки графиков функций, а также графиков кривых вторых, третьих и высших порядков. Причем достаточно часто требуется на одном экране отобразить сразу несколько графиков. Это может быть реализовано в виде нескольких областей экрана, в которые выводится соответствующий график. Для этого нужно про-

думать и написать процедуру DrawUserFunc (x1,x2,y1,y2:Real; X0, Y0, Mx, My:Integer; Func: FuncToDraw), которая выводит в прямоугольник с левой верхней вершиной в точке X0, Y0 размером MX на MY график функции Func на интервале [x1,x2] со значениями в диапазоне [y1,y2]. Для вычисления произвольной функции, как правило, определяется некоторый пользователь-

ский тип FuncToDraw.

Анализ требований и формальная постановка задачи. Нуж-

но построить график функции Func(x) и отобразить его в окне произвольного размера. Первым делом необходимо пересчитать координаты исходной функции в заданном диапазоне в целочисленные координаты позиций на экране. Алгоритм будем строить с учетом его дальнейшего использования для прорисовки кривых второго, третьего и высших порядков.

Для отображения графика на экране будем пользоваться следующим правилами.

1. Если в позиции экрана y = f(x), то выводим точку графика функции красным (либо на ваш выбор) цветом, например так:

Image1.Canvas.Pixels[x, y]:=clRed;

39