
шпоры по высшей математике 1 семестр 1 курс
.docx
31. Бесконечно-малые функции.
Бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
Функция α(x) – бесконечно-малая при x→a, если lim α(x) = 0.
Терема об отношении 2 бесконечно-малых функций
Предел отношения 2 бесконечно-малых функций = пределу отношения 2 других бесконечно-малых функций, соотв. им пропорционально.
α1(x)
 α2(x)
и β
1(x)
α2(x)
и β
1(x)
 β
2(x)
β
2(x)
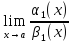 =
=
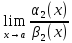
32. Замечательные пределы.
1)
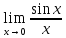 =1
2)
=1
2)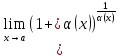
Раскрытие неопределённостей
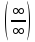 ,
,
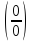 можно раскрыть используя правило
Лапиталя; разделяя каждый элемент на
x
в большей степени.
можно раскрыть используя правило
Лапиталя; разделяя каждый элемент на
x
в большей степени.
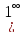 )
можно раскрыть используя 2 замечательный
предел.
)
можно раскрыть используя 2 замечательный
предел.
( сначала при помощи различных преобразований
приводим к
сначала при помощи различных преобразований
приводим к
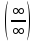 ,
,
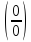 ,
и раскрываем.
,
и раскрываем.
33. Непрерывность функции в точке
Функция называется непрерывной в точке, если: функция определена в точке и ее окрестности; существует конечный предел функции в точке; этот предел равен значению функции в точке.
Свойства непрерывных функций
Точка, в которой функция не является непрерывной, называется точкой разрыва.
Если функция непрерывна и справа и слева, то она непрерывна в этой точке.
Если
функция y=f(x)
находится на отрезке
 непрерывна в точке a
справа.
непрерывна в точке a
справа.
Если
функция y=f(x)
находится на отрезке
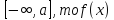 непрерывна в точке a
слева.
непрерывна в точке a
слева.
34. Непрерывность фун. на интервале
Функция называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.
Основные теоремы непрерывных функций
1)
Пусть заданы две функции f(x) и g(x) ,
непрерывные на некотором множестве X.
Сумма, произведение и частное (при
условии, что g(x)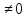 )
является также непрерывной функцией
на рассматриваемом множестве.
)
является также непрерывной функцией
на рассматриваемом множестве.
2) Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.
3)
Пусть функция z=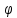 (x)
непрерывна
в точке x0,
а функция y=f(x)
непрерывна в точке z0,
где z0=
(x)
непрерывна
в точке x0,
а функция y=f(x)
непрерывна в точке z0,
где z0=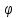 (x0),
тогда сложная функция y=f(
(x0),
тогда сложная функция y=f(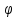 (x))
является непрерывной в точке x0.
(x))
является непрерывной в точке x0.
35. Производная функции
Это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Если функция имеет производную в точке x0, то в этой точке она непрерывна. Производная в точке 0 не существует.
Геометрический и механический смысл производной
1) Геометрический смысл: производная представляет собой угловой коэффициент касательной к графику функции y=f(x) в точке x0.
2)
Механический смысл: скорость – это
производная координаты по времени:
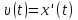
36. Основные правила дифференцирования
1) Пусть u(x) и v(x) – дифференциальные функции в точке x, тогда их произведение и частное также дифференцируемы в точке x.
2)
Пусть сложная функция y=f(z),
где z= (x)
дифф-мы в точке z,
тогда y=f(
(x)
дифф-мы в точке z,
тогда y=f(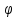 (x))
дифф-ма в точке x.
(x))
дифф-ма в точке x.
3) Постоянный множитель c можно выносить за знак производной.
4) Производная от суммы (разности) функции = сумме (разности) производных.
37. Производная сложной и обратной функции
1)
Пусть сложная функция y=f(z),
где z=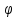 (x)
дифф-мы в точке z,
тогда y=f(
(x)
дифф-мы в точке z,
тогда y=f(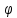 (x))
дифф-ма в точке x.
Производную сложной функции можно
найти по формуле: y'=y'z*z'x.
(x))
дифф-ма в точке x.
Производную сложной функции можно
найти по формуле: y'=y'z*z'x.
2) Если функции y=f(x) и x=g(y) — пара взаимно обратных функций, и функция y=f(x) имеет производную f'(x), то производная обратной функции находится по формуле: g'(x)=1/f '(x).
38. Дифференцирование неявных функций и функций, заданных параметрически
1) Чтобы найти производную функции, заданной неявно (когда слева и справа есть переменная y) каким-либо уравнением необходимо взять производную из обоих частей уравнения, затем переносим все y' влево и подставляем вместо y исходное выражение.
2) Пусть y=y(x) задана параметрически:
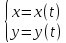 ,
тогда чтобы продифференцировать эту
функцию необходимо воспользоваться
формулой:
y'x=
,
тогда чтобы продифференцировать эту
функцию необходимо воспользоваться
формулой:
y'x=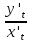
39. Дифференциал функции и её геометрический смысл
1) Пусть функция y=f(x) дифференцируема в точке x0, тогда превращение можно представить в виде
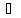 y=f
'(x0)*
y=f
'(x0)*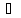 x+0(
x+0(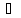 x)
x)
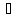 y
y f
'(x0)*
f
'(x0)* x
при
x
при
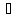 x→0
x→0
f
'(x0)* x
в разложении
x
в разложении
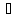 y
называется главной линейной относительно
y
называется главной линейной относительно
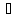 х
частью превращения функции.
х
частью превращения функции.
Главная
линейная относительно
 х
функция наз. дифф-ой функцией и
обозначается dy.
dy=y'*dx. y'=
х
функция наз. дифф-ой функцией и
обозначается dy.
dy=y'*dx. y'=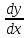
2)
Дифференциал функции y=f(x) в
точке x
равен приращению ординаты касательной
к графику функции в этой точке, когда x
получит приращение
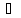 х.
х.
40. Производные высших порядков
Производная от производной 1-го порядка называется производной 2-го порядка. y'=f '(x); y''=(y')'; yn=(yn-1)'
Дифференцируемость функции
Пусть
функция y=f(x) дифф-ма в точке x0,
тогда превращение можно представить
в виде
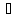 y=f
'(x0)*
y=f
'(x0)*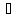 x+0(
x+0(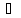 x)
x)
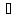 y
y f
'(x0)*
f
'(x0)* x
при
x
при
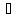 x→0
x→0
f
'(x0)*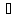 x
в разложении
x
в разложении
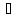 y
называется главной линейной относительно
y
называется главной линейной относительно
 х
частью превращения функции.
х
частью превращения функции.
Главная
линейная относительно
 х
функция наз. дифф-ой функцией и
обозначается dy.
х
функция наз. дифф-ой функцией и
обозначается dy.
1
порядка)
dy=y'*dx. y'=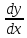
высших порядков) d2y=y''dx2; d3y=y'''dx3
41. Теорема Ролля и Лагранжа
1) Пусть f(x) удовлетворяет условиям: определена и непрерывна на отрезке [a,b]; дифф-ма на (a,b,); Значения функции на концах отрезков совпадают f(a)=f(b). Тогда существует точка c=(a,b) такая что f'(x)=0
2)
Пусть f(x)
удовлетворяет условиям: определена и
непрерывна на отрезке [a,b];
дифф-ма на (a,b,).
Тогда существует точка c
такая, что
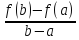 =f
'(c)
=f
'(c)
Правило Лопиталя
Правило
Лопиталя используется при вычислении
предела функции и относится только для
раскрытия неопределённостей:
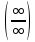 ,
,
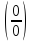 Такие пределы вычисляются по формуле:
Такие пределы вычисляются по формуле:
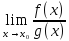 =
=
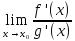
42. Условие монотонности функции.
Пусть
f(x)
определена и непрерывна на отрезке
[a,b],
тогда если: 1) f(x)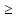 0,
для всех x
принадлежащих (a,b),
то f(x)
– не убывает; 2) f(x)
0,
для всех x
принадлежащих (a,b),
то f(x)
– не убывает; 2) f(x)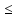 0,
для всех x
принадлежащих (a,b),
то f(x)
– не возрастает;
0,
для всех x
принадлежащих (a,b),
то f(x)
– не возрастает;
Следовательно:
если f(x)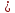 0,
для всех x
принадлежащих (a,b),
то f(x)
– возрастает; а f(x)
0,
для всех x
принадлежащих (a,b),
то f(x)
– возрастает; а f(x)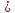 0
-
убывает
0
-
убывает
Необходимое условие экстремума
Пусть x0 – точка локального экстремума функции f(x), тогда f '(x) обращается в 0 или не существует.
Критические точки - те, которые не входят в обл. определения (чаще всего это точки разрыва). Стационарные-точки в которых значение производной равно нулю (точки экстремума)
43. Экстремум фун. одной переменной
Пусть
у нас есть функция y=f(x)
и точка x0
– точка локального max
(min)
если существует x
принадлежащий дельта-окрестности x0,
то f(x0)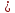 f(x)
max;
f(x0)
f(x)
max;
f(x0)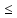 f(x)
min
f(x)
min
Локальные max и min – локальные экстремумы. x0 – точка локального максимума если f(x0)= максимальному значению f(x).
Достаточные условия экстремума
1) Пусть функция f(x) непрерывна в точке x0 и имеет конечную производную f'(x). Если же при переходе через точку x0 производная не меняет знак, то в точке x0 нет экстремума.
2) Пусть функция f(x) дважды дифференцируема в точке x0, причем
df(x0) = 0, а d2f(x0) > 0 (d2f(x0) < 0 ).
Тогда точка x0 есть точка локального минимума (локального максимума) функции f(x).
3) Пусть функция f(x) имеет в точке х0 производные f '(x0) и f''(x0), причем f'(x0) = 0, а f''(x0) > 0 (f''(x0) < 0 ).
Тогда точка x0 есть точка локального минимума (локального максимума) функции f(x).
44. Выпуклость и вогнутость графика функции. Точки перегиба
График функции y=f(x) называется вогнутым на (a,b) если он расположен ниже касательной, проведённой к графику функции.
График функции y=f(x) называется выпуклым на (a,b) если он расположен выше касательной, проведённой к графику функции.
Точка перегиба функции – это точка, в которой функция непрерывна и её график имеет касательную (которая может быть параллельна оси) и при переходе через (x) функция меняет направление выпуклости.
45. Асимптоты графика функции.
Асимптота – значение, к которому стремится функция. Различают вертикальные, горизонтальные и наклонные асимптоты.
Прямая
называется вертикальной
асимптотой, если 1 из односторонних
пределов в этой точке =
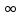 .
.
Прямая
называется горизонтальной
асимптотой функции, если предел этой
функции при x→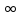 = числу.
= числу.
Прямая y=kx+b называется наклонной асимптотой, если существуют конечные пределы.
Схема исследования функции
1) Находим область определения функции.
2) Определяем чётность\нечётность функции и её периодичность.
3) Находим точки пересечения с осями Ox и Oy (приравниваем x=0 и y=0)
4) Исследуем функцию на наличие асимптот
5) Определяем y' и её критические точки (y'=0)
6) Находим y'' и её критические точки.
7) Результаты заносим в таблицу.
8) С помощью таблицы строим график функции.
