
§ 2.3. Нормальный закон распределения
В теории вероятностей и математической статистике, в различных приложениях важную роль играет портальный закон распределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность вероятности ее имеет вид
![]()

Кривая нормального закона распределения имеет колоколообразную форму (рис. 2.1), симметричную относительно прямой х =а (центр рассеивания). В точкех =а функция достигает максимума:
![]()
По мере возрастания х - а функция f(x) монотонно убывает, асимптотически приближаясь к нулю. С уменьшением криваястановится все более и более островершинной. Изменение а при постоянной не влияет на форму кривой, а лишь сдвигает ее вдоль оси абсцисс. Площадь, заключенная под кривой, согласно условию нормировки, равна единице. На рисунке 2.1 изображены три кривые. Для кривых1 и2 а = 0, эти кривые отличаются значением (1 < 2); кривая 3 имеет а 0 ( = 2).
Вычислим функцию распределения (2.19) для этого случая:

(2.23)
Обычно используют
иное выражение функции нормального
распределения.
Введем новую переменную
![]() ,
следовательно,
dx
=
dt.
Подставив
эти значения в (2,23), получим
,
следовательно,
dx
=
dt.
Подставив
эти значения в (2,23), получим
![]()
(2.24)
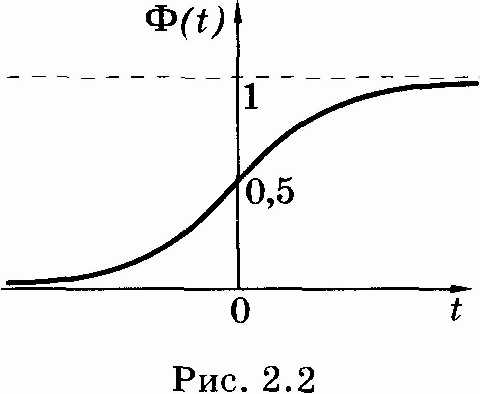
Значения функции Ф(t) обычно находят в специально составленных таблицах (см. [2]), так как интеграл (2.24) через элементарные функции не выражается. График функции Ф(t)изображен на рисунке 2.2.
На основании (2.17) можно вычислить вероятность того, что случайная величина при нормальном распределении находится в интервале(х1, х2). Без вывода, по аналогии с (2.24), укажем, чтоэта вероятность равна
![]() (2.25)
(2.25)
Воспользуемся выражением (2.25) для вычисления следующих вероятностей

Р = 2 • 0,8413-1 = 0,683; (2.26а)

По таблице находим Ф(2) = 0,9772, откуда
Р = 2 • 0,9772 - 1 = 0,954; (2.26б)

По таблице находим Ф(3) = 0,9986, откуда
Р = 2 • 0,9986 - 1 = 0,997. (2.26в)
На рисунке 2.3 приведено нормальное распределение (а = 0) и штриховкой показаны области, площади которых равны вероятностям 0,683 и 0,954.
Допустим, что произвольно
из нормального распределения выбираются
группы по п
значений
случайных величин. Для каждой группы
можно найти средние значения, соответственно
х1,
х2,
..., xi,
... . Эти
средние значения сами образуют нормальное
распределение
(в отличие от изложенного выше нормального
распределения
здесь каждому среднему значению xi
будет
соответствовать не вероятность,
а относительная частота). Математическое
ожидание
такого «нового» нормального распределения
равно математическому ожиданию
исходного нормального распределения,
а дисперсия (Dn)
и
среднее квадратическое отклонение (п)
отличаются
соответственно в n
в
![]() раз
относительно этих характеристикисходного
распределения:
раз
относительно этих характеристикисходного
распределения:

![]() (2.27)
(2.27)

Это положение здесь не доказывается, но его можно проиллюстрировать рисунком 2.4, на котором приведены графики нормальных распределений, полученных для групп со значениями п, равными 1, 4, 16, и п . Рассмотрим крайние частные случаи. При /г=1 приходим к исходному нормальному распределению, поэтому оп = о. При п п 0; фактически в этом случае «группа случайных величин» — это все исходное распределение, других групп нет, поэтому среднее значение выражается только одним числом и оно соответствует математическому ожиданию. Все распределение сводится к этому значению математического ожидания (на графике представлено вертикальной линией).
