- •Тульский государственный университет
- •Содержание
- •1. Описание численных методов
- •1.1. Метод левых прямоугольников
- •1.2. Метод трапеций
- •1.3. Метод Симпсона
- •1.4. Метод Чебышева
- •2. Блок-схема алгоритма основной программы:
- •4. Результат работы программы в виде графика
- •5. Результат работы программы в виде таблицы
- •6. Теоретическая часть
- •Assign(out, ‘out.Dat’);
- •Rewrite(out);
- •Write(out,’’); Writeln(out,’ ‘);
- •Список использованной литературы
1.1. Метод левых прямоугольников
Пусть
на отрезке
 задана непрерывная функция
задана непрерывная функция .Требуется вычислить определенный
интеграл
.Требуется вычислить определенный
интеграл
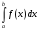 .
.
Разделим
отрезок
 точками
точками ,
, ,
, ,
…,
,
…, на
на равных частей длины
равных частей длины :
:
 .
.
|
Рис.2. |
Рис. 3. |
Обозначим
далее через
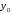 ,
,
 ,
, ,
...,
,
...,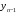 ,
, значение функции
значение функции в точках
в точках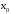 ,
, ,
, ,
…,
,
…, ,
т.е.
,
т.е.
 ,
,
 ,…,
,…, .
.
Составим суммы:
 ,
,
 .
.
Каждая
из этих сумм является интегральной
суммой для
 на отрезке
на отрезке и поэтому приближенно выражает интеграл
и поэтому приближенно выражает интеграл
 , (3)
, (3)
 . (4)
. (4)
Из
рис. 2 и 3 ясно, что если
 –
положительная и возрастающая функция,
то формула (3) выражает площадь ступенчатой
фигуры, составленной из «входящих»
прямоугольников, и эта формула называетсяформулой левых прямоугольников, а
формула (4) – площадь ступенчатой фигуры,
состоящей из «выходящих» прямоугольников,
и называетсяформулой правых
прямоугольников.
–
положительная и возрастающая функция,
то формула (3) выражает площадь ступенчатой
фигуры, составленной из «входящих»
прямоугольников, и эта формула называетсяформулой левых прямоугольников, а
формула (4) – площадь ступенчатой фигуры,
состоящей из «выходящих» прямоугольников,
и называетсяформулой правых
прямоугольников.
Ошибка,
совершаемая при вычислении интеграла
по формуле прямоугольников, будет тем
меньше, чем больше число
 (т. е. чемменьше
шаг деления
(т. е. чемменьше
шаг деления
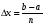 ).
).
1.2. Метод трапеций
Пусть
на отрезке
 задана непрерывная функция
задана непрерывная функция .Требуется вычислить определенный
интеграл
.Требуется вычислить определенный
интеграл
 .
.
Разделим
отрезок
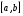 точками
точками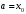 ,
, ,
, ,
…,
,
…, на
на равных частей длины
равных частей длины :
:
 .
.

Рис. 4.
Обозначим
далее через
 ,
,
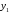 ,
, ,
...,
,
..., ,
, значение функции
значение функции в точках
в точках ,
, ,
, ,
…,
,
…, ,
т.е.
,
т.е.
 ,
,
 ,…,
,…, .
.
Составим сумму прямоугольных трапеций:
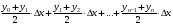 .
.
Эта
сумма является интегральной суммой для
 на отрезке
на отрезке ,
и поэтому приближенно выражает интеграл
,
и поэтому приближенно выражает интеграл
 . (5)
. (5)
Это
и есть формула трапеции. Ошибка,
совершаемая при вычислении интеграла
по формуле трапеции, будет тем меньше,
чем больше число
 (т. е. чемменьше
шаг деления
(т. е. чемменьше
шаг деления
 ).
).
1.3. Метод Симпсона
Разобьем
отрезок интегрирования
 на четное число
на четное число равных частей с шагом
равных частей с шагом .
На каждом отрезке
.
На каждом отрезке ,
,
 ,
...,
,
...,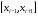 ,
...,
,
...,
 подынтегральную функцию
подынтегральную функцию заменим интегральным многочленом второй
степени:
заменим интегральным многочленом второй
степени:
 ,
,
 .
.
Коэффициенты
этих квадратных трехчленов могут быть
найдены из условий равенства многочлена
в точках
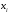 в соответствующих табличным данным
в соответствующих табличным данным .
В качестве
.
В качестве можно
принять интерполяционный многочлен
Лагранжа второй степени, проходящий
через точки
можно
принять интерполяционный многочлен
Лагранжа второй степени, проходящий
через точки ,
, ,
, :
:
 .
.
Элементарная
площадь
 может быть вычислена с помощью
определенного интеграла. Учитывая
равенство
может быть вычислена с помощью
определенного интеграла. Учитывая
равенство ,
получаем:
,
получаем:
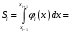

 .
.
Проведя
такие вычисления для каждого элементарного
отрезка
 ,просуммируем полученные выражения:
,просуммируем полученные выражения:
 .
.
Данное
выражение для
 принимается в качестве значения
определенного интеграла
принимается в качестве значения
определенного интеграла
 .
.
Полученное соотношение называется формулой Симпсона.
1.4. Метод Чебышева
П.Л. Чебышев предложил формулу:
 ,
,
в
которой коэффициенты
 фиксированы, а
фиксированы, а подлежат определению.
подлежат определению.
Рассмотрим
случай, когда
 ,
, ,
, .
Тогда:
.
Тогда:
 . (6)
. (6)
Коэффициент
 и точки
и точки определяются из условия, что это равенство
является точным для случая, когда
определяются из условия, что это равенство
является точным для случая, когда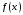 многочлен степени не выше
многочлен степени не выше :
:
 .
.
Подставляя
 в левую часть и интегрируя, получаем:
в левую часть и интегрируя, получаем:
 .
.
Подставляя полученный результат в правую часть (6), получим:


Тогда имеем:
 .
.
Это
равенство должно выполняться при любых
 ,
, ,
…,
,
…, ,
поэтому получаем следующую систему
уравнений:
,
поэтому получаем следующую систему
уравнений:
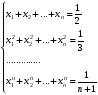
Пользуясь
алгебраическими свойствами симметричных
многочленов, можно привести эту систему
к одному алгебраическому уравнению
 -ой
степени, корни которого и являются
узлами квадратурной формулы Чебышева.
Опустив преобразования, ограничимся
готовыми результатами. В таблице
приведены значения узлов квадратурной
формулы Чебышева для 4 разбиений.
-ой
степени, корни которого и являются
узлами квадратурной формулы Чебышева.
Опустив преобразования, ограничимся
готовыми результатами. В таблице
приведены значения узлов квадратурной
формулы Чебышева для 4 разбиений.
|
|
|
|
|
|
|
0.083751 |
0.312730 |
0.500000 |
0.687270 |
0.916249 |
Для любых пределов интегрирования имеем:
 ,
,
где
 ,
, .
.
Значения
 берутся из таблицы при выбранном значении
берутся из таблицы при выбранном значении .
Для повышения точности можно не только
увеличивать количество узлов, но и
разбивать отрезок
.
Для повышения точности можно не только
увеличивать количество узлов, но и
разбивать отрезок на
подотрезки, к каждому из которых
применяется соответствующая формула.
на
подотрезки, к каждому из которых
применяется соответствующая формула.