Методичні рекомендації до розв’язування задач.

Приклад 1. Скласти параметричні та канонічні рівняння прямої, що проходить через точку М_о (2, -5, 8) перпендикулярно площині 3х + 4у – 7z – 6 = 0.

Розв'язання.

В якості направляючого вектора прямої можна взяти нормальний вектор (3, 4, -7) даної площини. Отримуємо х = 2 + 3t, у = -5 + 4t, z = 8 – 7t. Виключаючи з цих рівнянь параметр t, отримуємо канонічні рівняння даної прямої:

Відповідь.

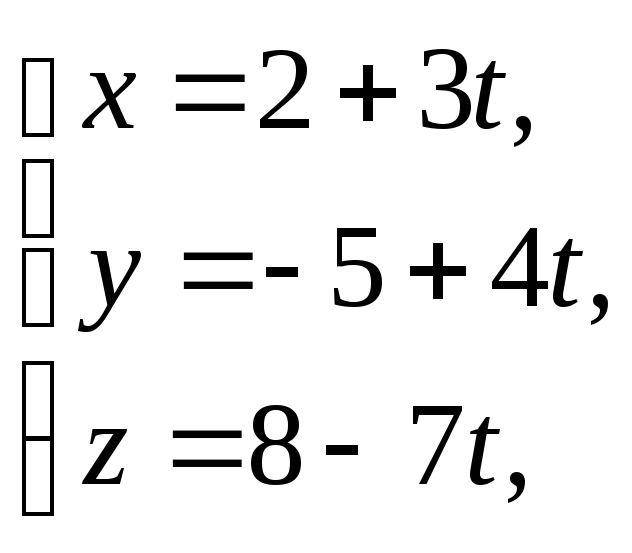
Приклад 2. Дано трикутник з вершинами А(1, 4, -5), В(-3, 6, 9), С(5, 6, 7). Скласти рівняння прямої, на якій лежить медіана, що проведена з вершини В.

Розв'язання. Знаходимо середину відрізка АС – точку D(3, 5, 1). Задача зводиться до знаходження прямої по двом точкам В та D. Отримаємо або .

Відповідь. .

Приклад 3. Знайти відстань між двома мимобіжними прямими: та

Розв'язання. Перша пряма походить через точку М₁ (3, -4, 5) та має направляючий вектор (1, 2, -2), друга проходить через точку М₂ (4, -2, 6) та має направляючий вектор (8, 6, 4). Звідси знайдемо

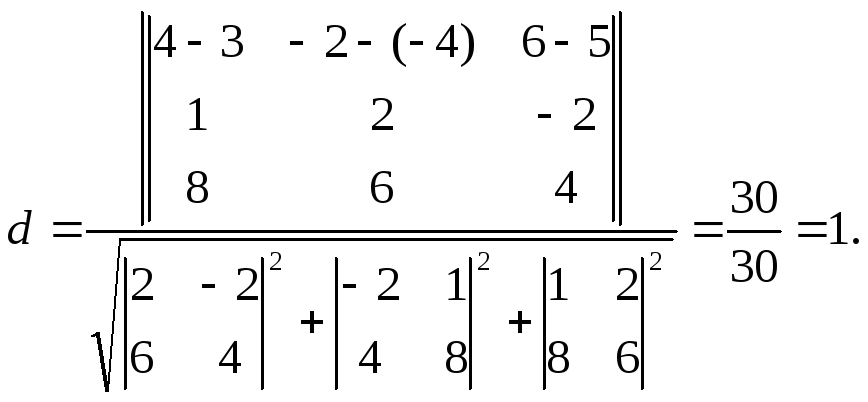
Відповідь. d =1.

Рис. 6.29

Приклад 4. Дослідити взаємне розміщення таких пар прямих:

А) і ;

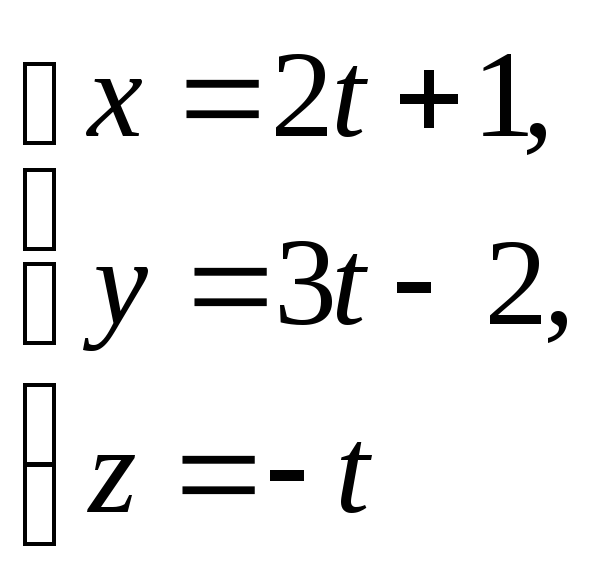Б) і ;

Розв'язання. А) Випишемо координати направляючих векторів даних прямих: (3, 2, -3), (2, -1, 3). Перевіримо умову :

– дана умова не виконана, тому прямі або перетинаються, або мимобіжні. Перевіримо, яка умова виконується. Маємо: М₁(3, -1, 1), М₂(5; -2, 4); (2; -1, 3).

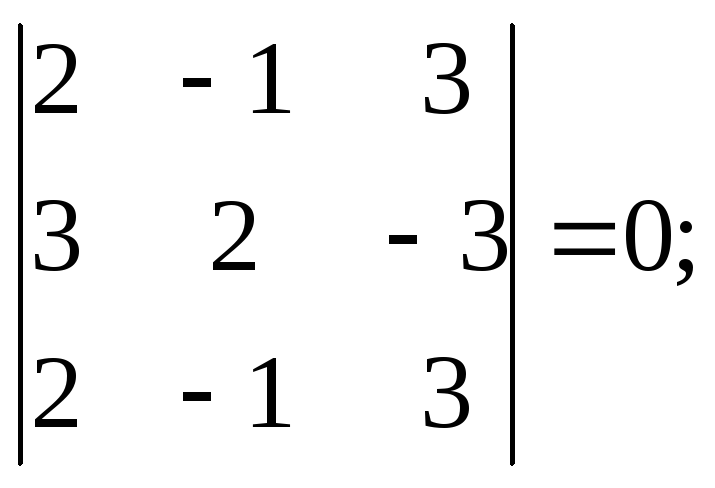Отже, виконується умова 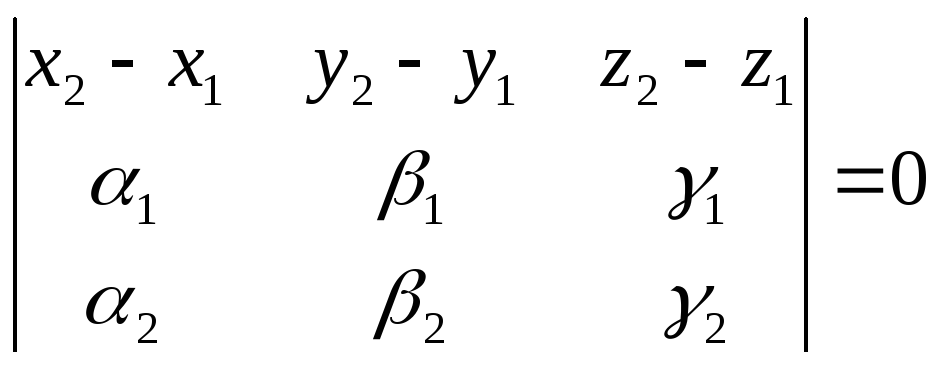, тому прямі перетинаються.

Б) У цьому випадку направляючі вектори такі: (2; 3; -1), (4; 3; 2). Оскільки відповідні координати цих векторів непропорційні, то прямі не паралельні. Тоді: М₁(1, -2, 0); М₂(1, 5, -1); (0, 7, -1);

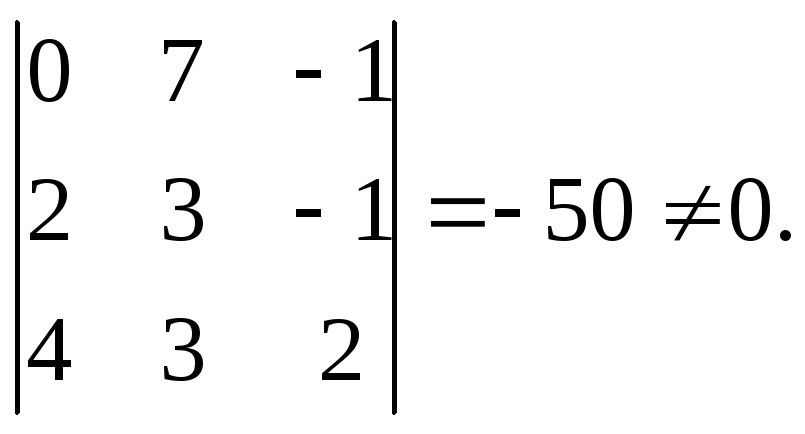Отже, прямі мимобіжні.

Відповідь. А) прямі перетинаються; Б) прямі мимобіжні.

Приклад 5. Знайти кут між прямою 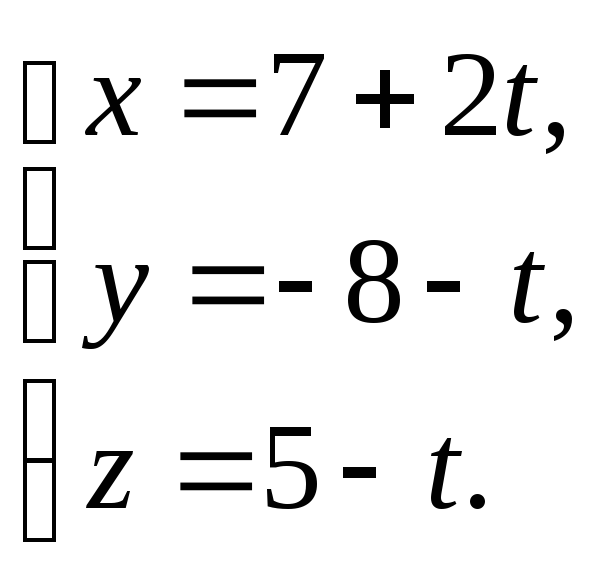та площиною 2х + 2у – 4z – 3 = 0.

Розв'язання. Скористаємося формулою sin  де α = 2, β = -1, γ = -1, А = 2, В = 2, С = -4, отримаємо:

sin  , =30⁰

Відповідь. =30⁰

Приклад 6. Перевірити, чи лежать прямі 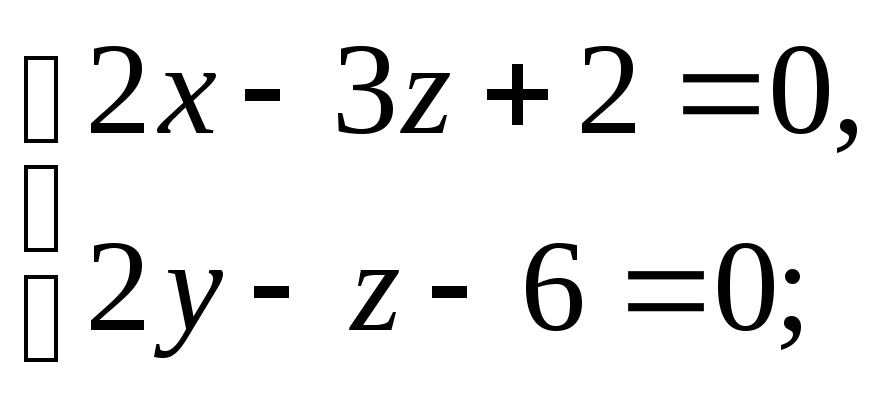та в одній площині.

Розв'язання. Зведемо рівняння заданих прямих l₁ та l₂ до канонічного вигляду, для чого знайдемо по одній точці на прямих і направляючі вектори цих прямих.

l₁:

Нехай z = 0, тоді:

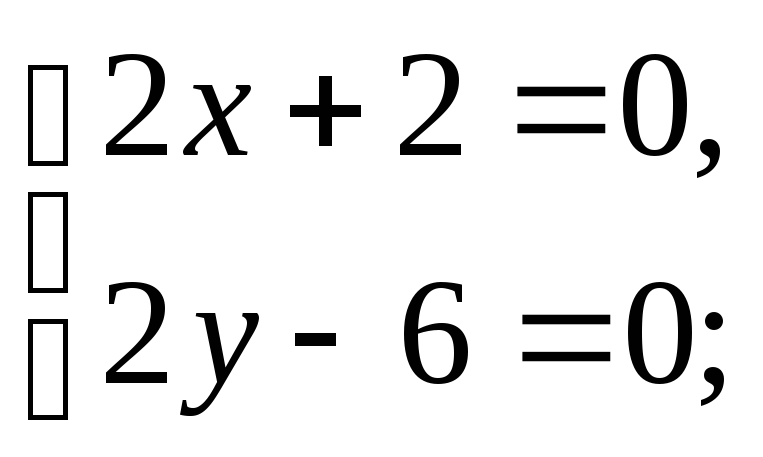
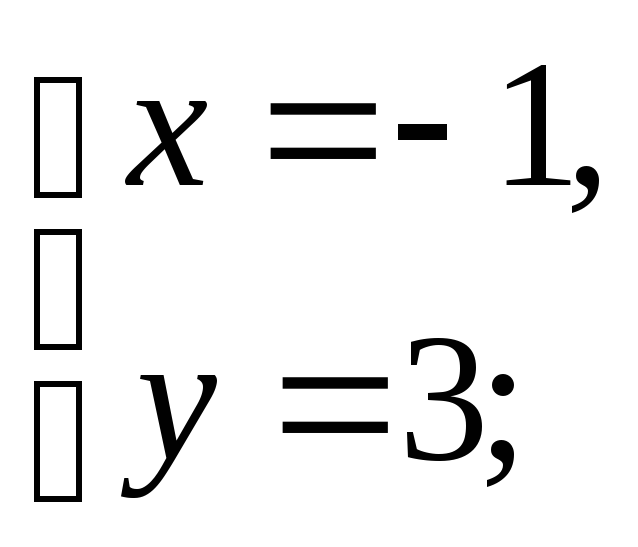
Тобто точка M_l (-1, 3, 0) належить прямій l₁. Далі знайдемо направляючий вектор прямої l₁.

= , де (2, 0, -3) – нормальний вектор площини 2х -3z + 2 = 0, а (0, 2, -1) – нормальний вектор площини

Отже, ; (6, 2, 4). Значить, канонічне рівняння прямої l₁ буде таким: або .

Аналогічно зведемо рівняння прямої l₂ до канонічного вигляду:

l₂:

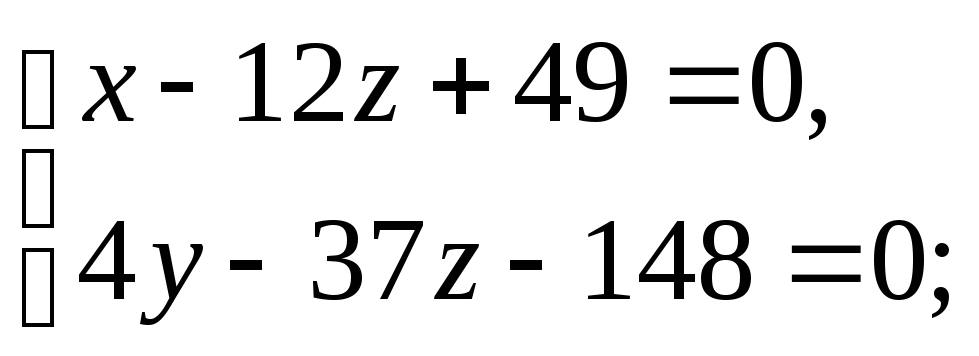
Нехай z = 0, тоді:

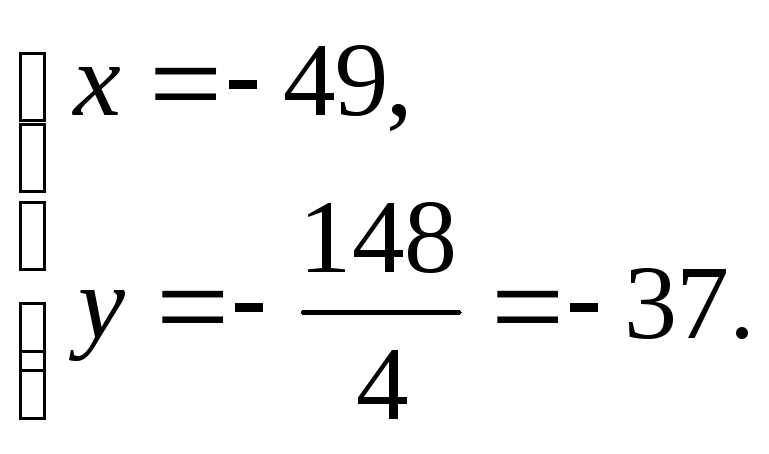
Тобто точка M₂ (-49, -37, 0) належить прямій l₂. Далі знайдемо направляючий вектор прямої l₂.

= , де – нормальний вектор площини , а – нормальний вектор площини

Отже,

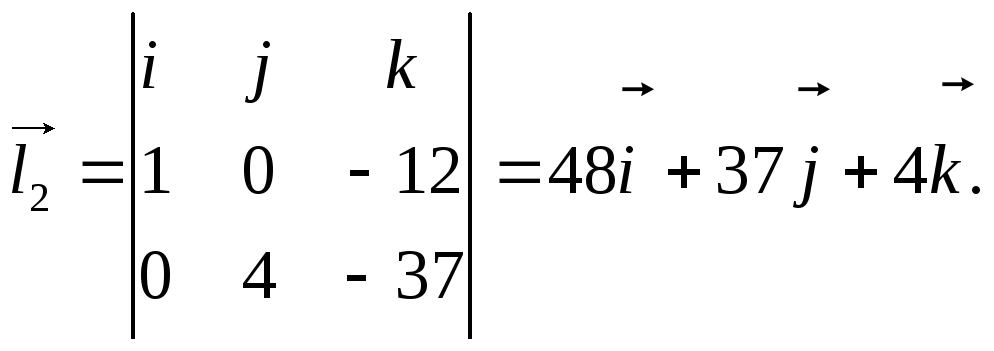
Тобто (48, 37, 4) – направляючий вектор прямої l₂, і її рівняння буде мати вигляд: .

Тепер перевіримо, чи лежать задані прямі в одній площині. Оскільки (), тоді досить перевірити вектори на компланарність. Для цього обчислюємо:

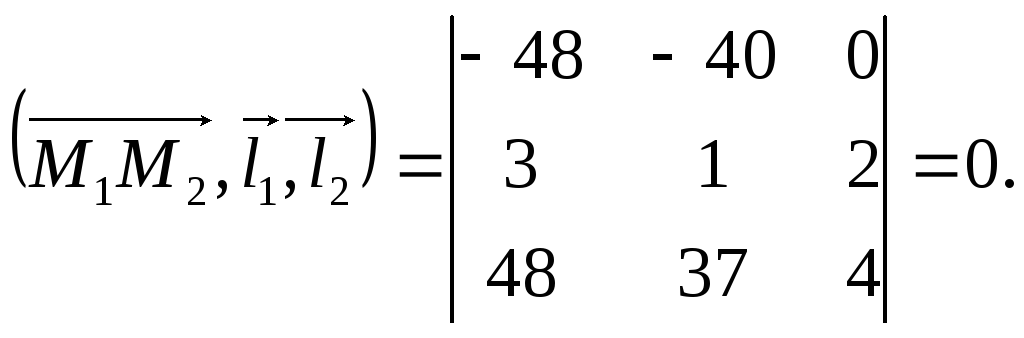
Отже, вектори – компланарні, а значить, прямі l₁ та l₂ лежать в одній площині.

Відповідь. Прямі l₁ та l₂ лежать в одній площині.

Приклад 7. Скласти рівняння площини, що проходить через точку M₁(4, -3, 1) паралельно прямим та

Розв'язання. Рівняння будь-якої площини, що проходить через дану точку М₁ (4; -3; 1), має вид: А(х – 4) + В(у + 3) + C(z – 1) = 0.

Шукана площина паралельна даним прямим, тому, застосовуючи умову

паралельності прямої та площини, матимемо:

та →

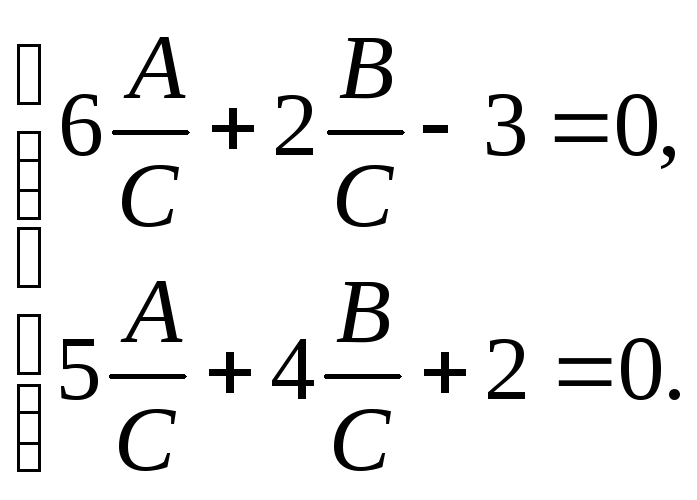Отримаємо 16х -27 у + 14z – 159 = 0.

Відповідь. 16х -27 у + 14z – 159 = 0.

Приклад 8. Знайти проекцію точки А(1; -3; 2) на площину 6x + 3y – z – 4l = 0.

Розв'язання. Проекцією даної точки на площину є точка перетину прямої, що проходить через дану точку перпендикулярно даній площині, з цією площиною.

Рівняння перпендикуляра будемо шукати у вигляді: , де координати направляючого вектора знайдемо з умови перпендикулярності прямої та площини чи

Отже, .

Знайдемо точку перетину прямої з площиною:

, звідки . Підставивши ці значення х, у та z у рівняння площини, знайдемо параметр t:

6(6t +1) + 3(3t – 3) – (-t + 2) – 41 = 0,

t = 1.

Знаючи параметр t, знайдемо проекцію точки А(1; -3; 2) на площину 6х + 3у – z – 41 = 0, ця точка А₁ (7; 0; 1).

Відповідь. А₁ (7; 0; 1).

Приклад 9. Скласти канонічні рівняння прямої, що лежить у площині xOz, проходить через початок координат та перпендикулярна до прямої

Розв'язання. Згідно умові, пряма проходить через початок координат, тому її канонічні рівняння мають вид: .

Так як пряма лежить у площині xOz, то β = 0. З умови перпендикулярності прямих слідує, що 3α + γ = 0, звідки γ = -3α . Підставимо у рівняння та скоротимо на α, отримаємо рівняння прямої: або .

Відповідь. .

Приклад 10. Скласти рівняння площини, яка проходить через: А) пряму і точку М (2, 0, 1); Б) дві паралельні прямі та

Розв'язання. А) Рівняння площини, яка проходить через точку М (2, 0, 1) має вигляд: А(х – 2) + Ву + C(z – 1) = 0.

Направляючий вектор прямої (1, 2, -1) і нормальний вектор площини (А, В, С) перпендикулярні, значить, їх скалярний добуток дорівнює 0.

А + 2В – С = 0.

Точка А(1, -1, -1) лежить на прямій, а значить, і на площині, тобто її координати задовольняють рівняння площини:

А (1 - 2) + (-1) + С (-1 – 1) = 0, або -А – В – 2С = 0.

Значить, А = -5С, В = 3С. Звідси шукане рівняння площини має вигляд:

(–5 (х – 2) + 3у + z – 1) С = 0, або 5х – 3у – z – 9 = 0.

Б) Взявши на одній з прямих точку, наприклад, на першій прямій точку М(1, 0 -2), отримуємо задачу, аналогічну з пунктом А). Шукана площина має рівняння 3х – 2у – 3 = 0.

Відповідь. А) 5х – 3у – z – 9 = 0; Б) 3х – 2у – 3 = 0.