§ 3.3 Скалярное произведение векторов

Определение 1. Пусть задано n-мерное векторное пространство ⁿ над полем действительных чисел и вектора ⁿ с координатами х=(х₁,х₂,…,x_n), у=(у₁,у₂,…,y_n). Выражение

= (х₁у₁ + х₂у₂ + … + x_ny_n),

называется скалярным произведением векторов и (число).

Определение 2. Если в n-мерном векторном пространстве ⁿ определено скалярное произведение, то такое векторное пространство называют евклидовым и обозначают Еⁿ.

Скалярное произведение векторов ⁿ удовлетворяет свойствам:

. . . .

. , если , и , если .

Определение 3. Длиной (нормой) вектора в называется число

= .

Вектор длиной равной единице, называется нормированным .

Определение 4. Углом между ненулевыми векторами  называется угол , принадлежащий промежутку и удовлетворяющий условию

.

Условие гарантирует единственное значение угла . Корректность определения косинуса угла между векторами евклидова пространства, т.е.условие  cos    1, вытекает из справедливости следующей теоремы

Теорема (неравенства Коши – Буняковского) В евклидовом пространстве выполнено:

или  cos    1, .

Доказательство. Рассмотрим функцию вида

F(t)= (a₁+ tb₁)²+ (a₂+ tb₂)² +…+(a_n+ tb_n)²

Произведя несложные преобразования, получим

F(t)= (a₁+a₁+…+a_n)²+ t²(b₁+ b₁ +…+ b_n)²+ 2t(a₁b₁ + a₂b₂ +…+ a_nb_n)

Так как F(t)  0, то дискриминант квадратической функции неположителен, т.е.

4(a₁b₁ + a₂b₂ +…+ a_nb_n)² – 4(a₁+ a₁ +…+ a_n )²(b₁+ b₁ +…+ b_n )²0

или

(a₁b₁ + a₂b₂ +…+ a_nb_n)²  (a₁+ a₁ +…+ a_n )²(b₁+ b₁ +…+ b_n )²

или

(a₁b₁ + a₂b₂ +…+ a_nb_n)  ((a₁+ a₁ +…+ a_n )²(b₁+ b₁ +…+ b_n )²)^0.5

или

(a, b)   a   b  или  cos    1, .

Определение 5. Вектора в евклидовом пространстве называются ортогональными, если их скалярное произведение равно нулю, т.е. = 0 (иными словами, они перпендикулярны).

Определение 6. Система векторов евклидова пространства называется ортогональной, если .

Определение 7. Система векторов ⁿ называется ортонормированной, если

.

Простейшей ортонормированной системой векторов будут орты i,j,k.

§ 3.4 Линейная независимость и базис

Евклидово пространство Еⁿ в наших условиях (мы работаем на множестве вещественных чисел с евклидовой метрикой)) можно отождествлять с линейным векторным пространством Rⁿ. Поэтому в дальнейшем тексте запись пространства символами Eⁿ или Rⁿ будем отождествлять.

Определение 1. Выражение называется линейной комбинацией системы векторов  Rⁿ с коэффициентами (числами)

Определение 2. Система векторов  Rⁿ называется линейно зависимой, если найдется их линейная комбинация, равная нулевому элементу , не все коэффициенты которой равны нулю.

Определение 3. Пусть задана система { a_j } n векторов c m координатами в векторном пространстве R^m вида {а_j=(а_1j,а_2j,…,а_mj)}, где второй индекс j = 1,…,n – представляет номера векторов, а первый индекс номер координаты. Тогда матрица А, столбцами которой являются координаты системы векторов,

называется координатной матрицей системы векторов { a_j }.

Отметим основные свойства линейно зависимых систем векторов:

1. Любое расширение линейно зависимой системы оставляет ее линейно зависимой (добавление вектора к такой системе не меняет ее тип)

2. Если два вектора коллинеарные, то они линейно зависимы.

3. Если в системе векторов присутствуют коллинеарные вектора, то система линейно зависима ( как расширение линейно зависимой).

4. Система векторов линейно зависима тогда и только тогда, когда в ней найдется вектор, представимый в виде линейной комбинации других векторов системы (доказать !).

5. Если среди векторов есть нулевой, то эти вектора линейно зависимы (нулевой вектор будет иметь ненулевой коэффициент ).

6. Система векторов будет линейно зависимой тогда и только тогда, когда ранг ее координатной матрицы меньше числа векторов.

7. Система векторов линейно зависима, если размерность вектора меньше числа векторов в системе

Последние два свойства следуют из теорем 2, 4 § 2.5.

Определение 4. Система векторов  R называются линейно независимыми, если равенство имеет место тогда и и только тогда, когда ( иными словами, при тривиальном наборе чисел).

Отметим основные свойства линейно независимых систем векторов:

1. Любое сужение линейно независимой системы оставляет ее линейно независимой.

2. Система векторов линейно независима тогда и только тогда, когда ранг координатной матрицы равен числу векторов системы.

Последнее свойство следуют из теоремы 1 § 2.5.

Рассмотрим совокупность многочленов степени не выше m с коэффициентами из некоторого поля К. Эти многочлены, относительно операций сложения и умножения на числа из К образуют линейное пространство. Многочлены 1, х, х², …,х^k составляют в пространстве многочленов степени не выше m линейно независимую систему, т.к. из равенства ₀1 + ₁х +..+ _kх^k=0 следует, что ₀=₁=...= _k=0.

Определение 5. Подпространством векторного пространства ⁿ над полем К называется любое непустое подмножество этого пространства, на котором определены операции сложения элементов и умножения элемента на число:

1) ; 2) .

Полезно заметить, что для геометрического трехмерного пространства всякое подпространство является либо прямой, либо плоскостью, проходящей через начало координат.

Само пространство можно рассматривать как свое собственное подпространство. Нулевое пространство ( состоящее из одного нулевого вектора) называют тривиальным подпространством пространства Rⁿ. Все остальные подпространства называют нетривиальными.

Простейший способ построения подпространств состоит в следующем. Берем в заданном векторном пространстве произвольные вектора и рассматриваем все их линейные комбинации. Обозначим совокупность этих комбинаций через М. Удаляя из М те вектора, которые линейно зависят от других векторов из М, мы получим линейно независимую систему в М.

Определение 6. Пусть М подпространство n-мерного векторного пространства Rⁿ и система векторов из М. Эта система называется базисом векторного подпространства М, если

1. Она линейно независима

2. Для любого вектора 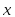из М существуют такие числа , что 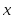линейно выражается через 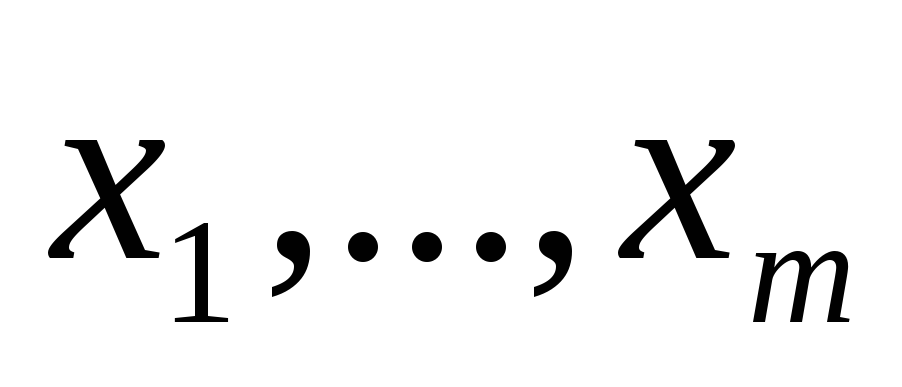,т.е. .

Иными словами, система векторов образует базис, если она линейно независима и через ее линейную комбинацию может быть представлен любой вектор подпространства.

При этом данная линейная комбинация называется разложением вектора по базису , а числа - координатами вектора в данном базисе.

Существует бесконечное число базисов данного линейного подпространства. В определении не требуется, чтобы базис состоял из заданного числа векторов. Однако справедлива следующая теорема

Теорема 1. Количество векторов в базисе линейного подпространства не зависит от выбора базиса.

Иными словами, количество векторов в базисе заданного подпространства зависит только от самого подпространства, а не от того, какие конкретные вектора выбраны в качестве базисных: количество векторов в каждом базисе векторного подпространства одно и тоже.

Определение 7. Пусть М векторное подпространство в Rⁿ, и {} – базис в М. Число m, равное количеству векторов в базисе М, называется размерностью векторного подпространства М.

Заметим, что размерность подпространства не превосходит размерности самого линейного пространства.

Пример. Рассмотрим пространство векторов R³ и некоторое подмножество в его подпространстве М, состоящее из 4 векторов

, , ,

Составим координатную матрицу системы векторов

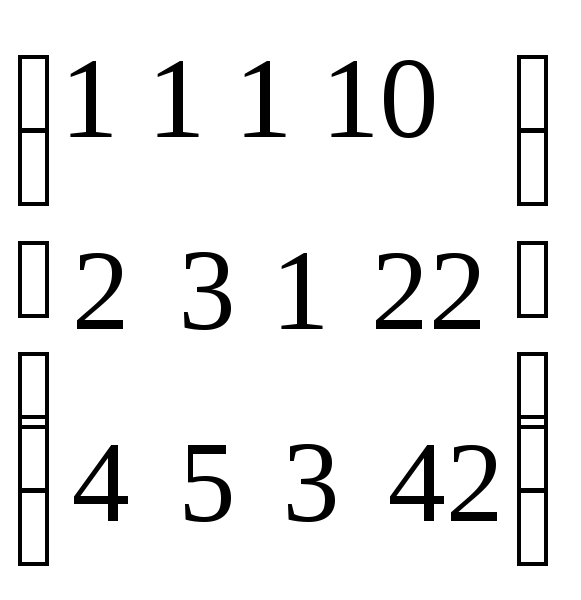
Произведя элементарные преобразования над строками матрицы, получим матрицу вида

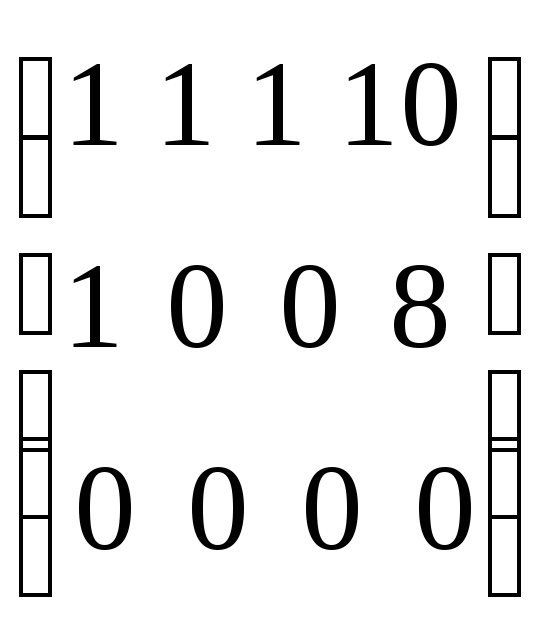
Второй и третий вектора линейно зависимы (коллинеарные). Линейно независимой системой векторов могут быть наборы из двух векторов с номерами (если удалим вектор 3):(1,2),(1,4),(2,4).

Так как размерность подпространства М равна максимальному числу линейно независимых векторов содержащихся в М, то в нашем примере размерность М равна двум. В качестве базиса можем выбрать любую из трех пар.

Если размерность подпространства совпадает с размерностью пространства, то любой из базисов подпространства будет базисом самого пространства.

Очевидно, что если - базис в подпространстве векторного пространства ⁿ размерности n и k < n, то можно выбрать элементы ⁿ так, что совокупность будет составлять базис всего пространства ⁿ.

( иными словами - любой базис подпространства может быть дополнен до базиса самого пространства).

Теорема 2. Система векторов {} образует базис, если она линейно независима и число векторов совпадает с их размерностью.

Доказательство. Пусть число векторов совпадает с размерностью пространства и т.к. система линейно независимая, то определитель координатной матрицы отличен от нуля (свойство 2 линейно независимых систем) , т.е. система

x₁ = а₁е₁₁ + а₂е₁₂ +…+ а_nе_1n

x₂ = а₁е₂₁ + а₂е₂₂ +…+ а_nе_2n

…………..

x_n = а₁е_n1 + а₂е_n2 +…+ а_nе_nn

имеет нетривиальное решение. Тогда для любого существует нетривиальный набор чисел , что .

Следствия:

1. Если векторное пространство Rⁿ имеет базис, состоящий из n элементов, то размерность Rⁿ равна n.

2. Система из n векторов в n-мерным пространстве образует базис, если определитель координатной матрицы системы отличен от нуля.

Замечание. Геометрическая интерпретация базиса: любой вектор в пространстве Rⁿ может быть представлен в виде линейной комбинации n векторов базиса.

Теорема 3. Каждый элемент векторного пространства может быть разложен по базису единственным способом (единственность разложения вектора по базису).

Доказательство. Пусть таких разложений по базисов два, т.е. существуют наборы чисел а₁, а₂,…,а_т и b₁, b₂,…,b_n , что

х = и х = или

= или

(

а так как система линейно независима, то все разности равны нулю. Иными словами, a_i = b_i для всех индексов.

Теорема 4. Любая ортонормированная система образует базис.

Доказательство. Для доказательства теоремы достаточно показать, что система из n векторов линейно независима. Рассмотрим линейную комбинацию

и последовательно будем умножать ее скалярно на вектора e_i. Получим:

Из свойства скалярного произведения

и следует, что x_i=0 i=1,…,n.

Следствие. Любая ортогональная система из n векторов образует базис (различие будет только в выражении ).

Определение 8. Базис вида

,

в пространстве Rⁿ называют каноническим базисом.