3.2.2. Недостижимые состояния.
Среди состояний автомата могут быть такие, которые недостижимы из начального состояния ни для какой входной цепочки. На рис 3.8 (а) и 3.8 (в) таким является состояние 4. Такие состояния называются недостижимыми и столбцы, соответствующие этим состояниям, можно удалить, получив автомат с меньшим числом состояний.
Для любого конечного автомата довольно просто составляется список достижимых состояний:
1. Начать список начальным состоянием.
2. Для каждого состояния, уже включенного в список, добавить все еще не занесенные в него состояния, которые могут быть достигнуты из этого нового состояния под действием каждого входного символа.
Если эта процедура перестает давать новые состояния, то все достижимые состояния уже получены, а все остальные можно удалить как недостижимые. Число шагов процедуры ограничено числом состояний.
Пример 3.4. На рис. 3.9 (а) приведена таблица переходов автомата с начальным состоянием s0. Сформируем для него список достижимых состояний, по предложенному алгоритму. Вначале занесем в список s0. Затем добавим к нему s1 и s5. Из s1 имеется переход в s2 и s7, а из s5 - в s3 и s1, причем новым является только состояние s3. Из s2, s7 и s3 нет переходов в новые состояния, следовательно, окончательный список достижимых состояний
s0 s1 s5 s2 s7 s3.
Оставшиеся состояния s4, s6 и s8 - недостижимы. Удалив соответствующие им столбцы, получим таблицу, представленную на рис. 3.9 (б).
Будем говорить, что автомат приведенный (минимальный), если он не содержит недостижимых состояний и никакие два его состояния неэквивалентны друг другу.
Если автомат не приведенный, то можно получить эквивалентный ему автомат, с меньшим числом состояний, либо исключая недостижимые состояния, либо объединяя эквивалентные в одно состояние. Приведенный автомат, полученный таким способом, имеет число состояний меньшее, чем исходный (если он уже не был приведенным), и может быть компактно реализован на вычислительной машине.
Метод нахождения недостижимых состояний, приведенный выше, достаточно эффективен. Однако, использовать тест эквивалентности для минимизации автоматов нецелесообразно, так как он позволяет обработать одновременно только два состояния. Далее предлагается более эффективный способ поиска и объединения эквивалентных состояний.
3.2.3. Метод разбиения
Этот метод состоит в разбиении множества состояний автомата на непересекающиеся подмножества или блоки, такие, что неэквивалентные состояния попадают в разные блоки. Рассмотрим этот метод на примере автомата, таблица которого представлена на рис. 3.10 (а).
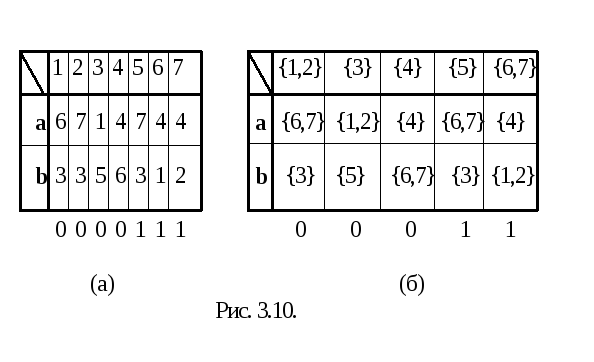
Сначала разбиваем множество его состояний на два блока, один из которых содержит отвергающие, а другой - допускающие состояния:
P0=({1,2,3,4},{5,6,7})
Ни одно из состояний первого блока неэквивалентно состояниям из второго блока, так как нарушается условие подобия. Посмотрим, что происходит с состояниями блока {1,2,3,4} под воздействием символа a. Состояния 3,4 переходят в состояния 1,4 из блока 1, а состояния 1,2 переходят в 6,7 из второго блока. Это означает, что для любого состояния из множества {1,2} и любого состояния из {3,4} соответствующие состояния - приемники неэквивалентны по входу a. Это нарушает условие преемственности и поэтому мы можем заключить, что ни одно из состояний {1,2} не эквивалентно ни одному из состояний {3,4}. Это позволяет провести новое разбиение:
P1=({1,2},{3,4},{5,6,7})
причем состояния из разных блоков всегда неэквивалентны.
Теперь попробуем найти такой входной символ и блок в P1, чтобы его можно было разбить на новые блоки, относительно этого входного символа. Так повторяем до тех пор, пока ни одно разбиение невозможно. Например, {3,4} из P1 разбивается относительно a и получается
P2=({1,2},{3},{4},{5,6,7})
Блок {5,6,7} из P2 разбивается относительно a или b и получается
P3=({1,2},{3},{4},{5},{6,7})
Полученное P3, не допускает дальнейшего разбиения. Действительно, блок {1,2} по a переходит в блок {6,7}, а по b - в {3}; блок {6,7} по a переходит в {4}, а по b - в {1,2}; остальные блоки имеют по одному состоянию.
Когда процедура разбиения закончена, состояния внутри каждого блока эквивалентны, то есть их можно объединить и получить минимальный автомат (см. рис. 3.10 (б)), так как недостижимых состояний в рассматриваемом примере не было. В общем случае процедура разбиения должна сопровождаться удалением недостижимых состояний в целях получения минимального автомата.
Попрактиковавшись, можно научиться опознавать эквивалентные состояния (нетерминалы), которые приводят к одной и той же ситуации, но каким бы ни было число ненужных состояний в автомате (нетерминалов в грамматике), с помощью предложенных алгоритмов всегда можно получить минимальное описание.