Дельта –функция

Дельта-функция определяется следующим образом

причем так, что интеграл

.

Очевидно, что пределы могут быть любые, охватывающие начало координат

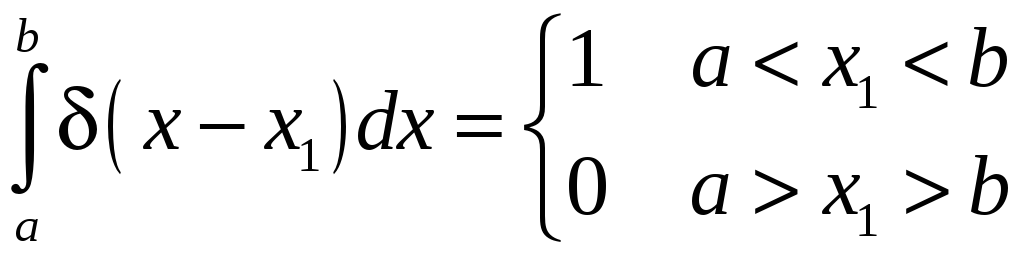
Из определения -функции следует, что если – любая непрерывная функция, то

, (22)

действительно

где – сколь угодно малая величина – .

-функция, четная функция, т.е. .

Действительно в соответствии с (22)

,

заменим в этой формуле на

Для -функции

действительно

.

-функция может быть получена как предел непрерывной функции

,

так как . а .

Трехмерная -функция равна нулю везде кроме начала системы координат, и интеграл по всему пространству равен 1.

Функция Грина

Функцией Грина называется некоторая вспомогательная функция, используемая при решении дифференциальных уравнений. Пусть у нас имеется уравнение Гельмгольца

(23)

Функция Грина удовлетворяет уравнению с той же правой частью и -функцией в качестве возбуждающего тока:

(24)

Это уравнение не определяет ещё полностью функцию G, нужно поставить ещё условия на границе области или условие излучения. Это можно сделать различным образом, то есть вводить для одного и того же уравнения различные функции Грина, мы вернёмся к этому ниже.

Функция Грина зависит от координат точки , по которой производится дифференцирование, и от координат точки , в которой располагается элементарный диполь, точнее –источник. В (24) играет роль параметра. При любых граничных условиях функция Грина симметрична:

что отвечает теореме взаимности: поле в точке , возбуждаемое источником, располагаемым в точке (левая часть), равно полю в точке , возбуждаемому источником, расположенным в точке (правая часть).

Использование функции Грина для решения основано на преобразовании объёмного интеграла в поверхностный по второй формуле Грина. Умножая (24) на и ( 23 ) на и вычтем из первого выражения второе

-

--------------------------------------------------------

Проинтегрируем по произвольной области V, содержащей точку

где см. ( 22 ).

В соответствии со второй формулой (теоремой) Грина

Область V ограничена поверхностью S. Внутри S U и U непрерывны и содержится точка . В конкретных задачах S должна содержать поверхность металлических тел и внешнюю поверхность, которую мы в некоторых случаях будем устремлять в .

(25)

Эта формула показывает, что для того, чтобы получить значения функции , то есть решение уравнения (23) в какой-либо точке , надо взять функцию Грина, порождаемую источником, расположенным именно в точке . Формула (25) даёт непосредственно решение (23), если G подчинить тем же условиям, на границе области, которым должно удовлетворять U. Например, если на поверхности S, окружающей объём и содержащей все источники , то для , тогда (25) примет вид:

(26)

Если на S и ,

то В (25) тоже равен 0.

Строго можно показать, что если U и G удовлетворяют одинаковым граничным условиям, то

.

Таким образом, применяя формулу (26), мы можем считать, что задача решена если она решена для –источника, то есть известна функция Грина данной задачи.

Функция Грина в вакууме при наложении условия излучения имеет вид

(27)

Физический смысл (26) очень прост. Функция Грина (27) – это поле точечного источника. Поле произвольного распределения источников находится как суперпозиция полей точечных источников.

Векторная функция Грина

Если линейное дифференциальное уравнение векторное, то при отыскании функции Грина в правую часть, кроме -функции, необходимо ввести ещё единичный вектор. Решение уравнения представляет собой вектор с тремя составляющими. Чтобы охватить все случаи, необходимо решить уравнение при трёх ориентациях единичного вектора в правой части. Таким образом, функция Грина в векторном случае определяется девятью скалярными величинами , которые образуют тензор второго ранга. По форме запись решения через тензорную функцию Грина остаётся такой же, как и в скалярном случае, но расшифровывается эта запись подобно тому, как расшифровывается тензорная связь между векторами и (4),(5).

Исключение из этого правила составляет функция Грина уравнения для векторного потенциала или вектора Герца

Нетрудно показать, что вектор и в этом случае всюду параллельны. Поэтому решение его может быть записано через скалярную, а не векторную функцию Грина.

где G определяется формулой (27).

Простота этой формулы обусловила широкое применение векторных потенциалов и вектора Герца . В неоднородных средах функция Грина векторного потенциала представляет собой тензор. И в этом случае применение векторного потенциала не упрощает решение задачи.

Функция Грина уравнения Максвелла.

Функция Грина уравнения Максвелла можно вводить двумя способами в зависимости от того, в какое из двух уравнений вводится -источник. Запишем два первых из уравнений Максвелла

1. |

2. |

В первом варианте вводим функцию Грина элементарного электрического диполя, обозначим, создаваемое при этом поле обозначим ( и ). Заменим в первом уравнении на -функцию, умноженную на единичный вектор .

3. |

4. |

Во втором варианте функцию Грина элементарного магнитного диполя, создаваемое при этом поле обозначим (,). Заменим во втором уравнении на -функцию, умноженную на единичный вектор .

Здесь принято вносить -источник с противоположным относительно первого случая знаком.

Применим лемму Лоренца в интегральной форме, то есть векторный вариант формулы Грина.

Для этого:

Умножим скалярно 4 на , 1 на , вычтем из 4–1

(28)

Умножим скалярно 2 на , 3 на , вычтем из 2–3

(29)

Вычтем из выражения ( 28 ) выражение ( 29 ).

При этом используем векторное тождество

.

В этом случае

;

и окончательно

.

Проинтегрируем по объёму, включающему точку

Аналогично можно получить:

Если интегрирование ведётся по бесконечному объёму, то интегралы

так как в бесконечности поле равно нулю. То же самое будет при интегрировании по бесконечному объёму, включающему металлические тела.