2.6. Выборочные дисперсия и среднеквадратичное отклонение

В реальном эксперименте имеет место выборка конечного объема, а не генеральная совокупность, подчиняющаяся нормальному закону. Поэтому чтобы воспользоваться формулой (2.12) для определения случайной доверительной погрешности результата измерения, необходимо найти оценку параметра и новые коэффициенты t_P, N (которые в этом случае будут зависеть от количества измерений N), соответствующие выборке конечного объема.

Таким наилучшим приближением, или оценкой стандартного отклонения , согласно (2.3) является величина

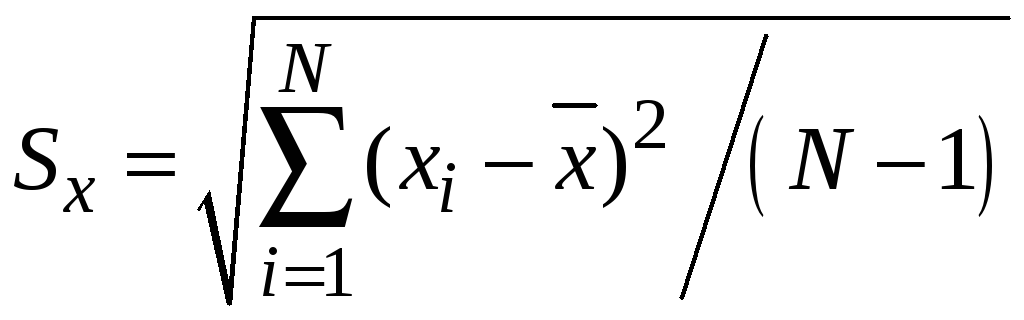, (2.13)

называемая выборочным среднеквадратичным отклонением (СКО x) результата наблюдения от среднего. Квадрат СКО называют выборочной дисперсией результата наблюдения.

Для нахождения оценки параметра рассмотрим случайную величину Z, представляющую собой сумму случайных величин X и У. Тогда среднее значение Z имеет вид

а выборочная дисперсия

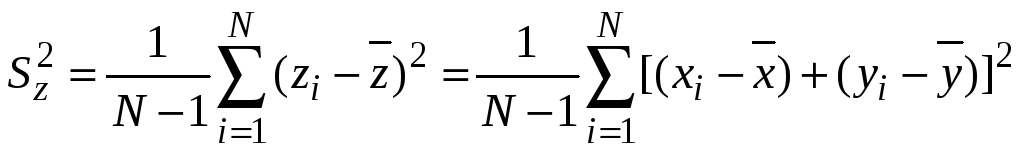
может быть представлена в виде

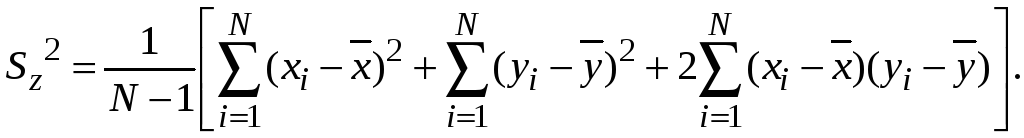
Если X и Y независимы друг от друга, то их отклонения от средних значений и также независимы. Учитывая, что среднее значение произведения независимых случайных величин равно произведению средних значений сомножителей, получим, что последняя сумма равна нулю, и S_z² = S_x² + S_y², т. е. дисперсии независимых случайных величин складываются линейно, а выборочные среднеквадратичные отклонения складываются квадратично.

Если Z = аХ + bY, то, повторив рассуждения, получим

S_z² = aS_x² + bS_y².

В случае суммы более двух случайных величин

Z = a₁X₁+a₂X₂ +…+a_NX_N = ,

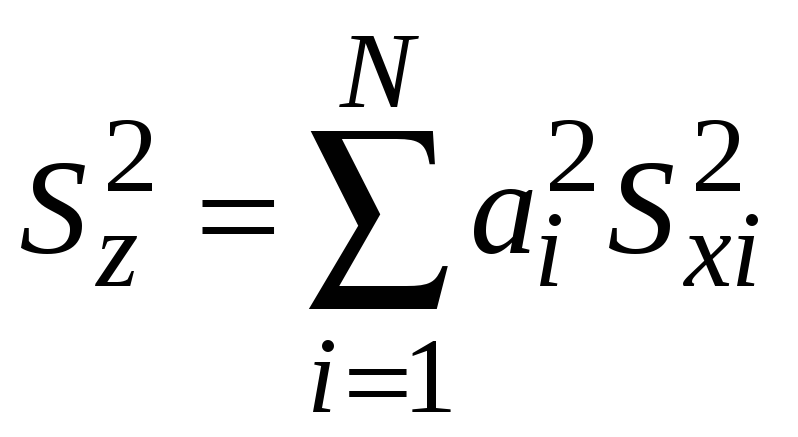. (2.14)

Для нахождения погрешности результата измерения представляет интерес не СКО результата отдельного наблюдения , а СКО сред­него значения . Взаимосвязь между параметрами и можно найти, если учесть, что среднее значение есть сумма N незави­симых случайных величин, дисперсии которых одинаковы

.

Тогда, ис­пользуя формулу (2.14), в которой а_i = 1/N, с учетом получим для дисперсии параметра :

.

Отсюда следует, что СКО

. (2.15)

Параметр , называемый выборочным среднеквадратичным отклонением среднего (СКО ), является наилучшим приближением к параметру .

Если СКО найдено согласно (2.15), то, как было впервые предсказано английским математиком В. С. Госсетом, писавшим свои работы под псевдонимом Стьюдент, и впоследствии доказано Р. А. Фишером, новая стандартизованная переменная имеет функцию плотности распределения вероятности , зависящую от объема выборки N. Вероятность того, что величина u попадет в заданный интервал (), будет

,

откуда случайную доверительную погрешность результата измерения необходимо рассчитывать по формуле

, с вероятностью P,

где – коэффициенты Стьюдента, зависящие от доверительной вероятности P и объема выборки N, по которой рассчитываются и . При больших значениях (на практике при N ≥ 20) параметры и , рассчитываемые по выборке конечного объема, переходят в параметры и нормального распределения, а коэффициенты Стьюдента t_P, N – в коэффициенты t_P для нормального закона.

Для проверочной оценки случайной доверительной погрешности ре­зультата измерения её расчет можно также производить по формуле x = _P, N R, где R = x_max – x_min – размах выборки.

Значения коэффициентов t_P, N и _P, N для данных значений дове­рительной вероятности (по договоренности в технике берут значение Р = 95 %) и числа N наблюдений в выборке приведены в приложении. В математических справочниках, как правило, коэффициенты Стьюдента приводят в таблицах в виде , где ν = N – 1 называется числом степеней свободы выборки объема N.

Необходимо отметить, что при расчетах доверительной погреш­ности по Стьюденту результаты наблюдений должны принадлежать генеральной совокупности, распределенной по нормальному закону, что может быть проверено с помощью специальных статистических критериев. Для выполнимости этой процедуры выборка должна быть достаточно представительной (от 50 наблюдений и больше). Выборки малых объёмов (N << 15), которые имеют место в работах лабо­раторного физического практикума, на принадлеж­ность нормальному распределению не проверяют.