Задача №1. Записать формулу функции f(x₁,x₂,x₃) и минимизировать ее геометрическим методом, методом карт Карно, Квайна, Квайна-Мак-Класки, неопределенных коэффициентов, минимизирующих карт. Сравнить результаты.

Решение:

1.Геометрический метод.

Данная функция задается следующей таблицей истинности:

x1
x2
x3
f(x1,x2,x3)

Ее формула в СДНФ имеет вид:

.

Отметим на рис.1 вершины, соответствующие конъюнкциям, входящим в СДНФ данной функции:

x₃

x₂

x₁

Рис.1

З

x₁

аметим, что четыре вершины лежат в одной грани (x₂), а две на одном ребре (x₁x₃).

Откуда следует, что минимальная форма функции и есть сумма этих интервалов x₂˅x₁x₃, т.е. f(x₁,x₂,x₃) _МДНФ = x₂˅x₁x_3. Другого варианта решения здесь не может быть. Задача решается однозначно.

2. Метод неопределенных коэффициентов.

.

Составим систему, в которой слева поместим координаты вершин (область определения функции). Верхние индексы коэффициентов комбинируем соответственно из записанных координат вершин с учетом взятых нижних индексов.

Из уравнений (1),(2),(5) в силу свойств дизъюнкции вытекает, что

.

Вычеркнем уравнения, в правой части которых стоят нули, а в остальных уравнениях вычеркнем коэффициенты равные нулю.

После этого система примет вид:

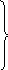
В полученной системе в силу свойства дизъюнкции можно приравнять единице коэффициент , тогда 1,2,4,5 уравнения этой системы превращаются в тождества, из третьего уравнения системы возьмем . Все остальные коэффициенты во всех уравнениях положим равными нулю:

Следовательно, мы нашли , остальные коэффициенты равны нулю. Отсюда минимальная форма данной функции:

f(x₁,x₂,x₃) _МДНФ= x₂˅x₁x_3.

3. Метод минимизирующих карт.

.

Строим для функции минимизирующую карту:

Отметим в последнем столбце те конъюнкции, которые входят в СДНФ данной функции. Вычеркнем неотмеченные строки, затем вычеркнем в остальных строках (действуя по столбцу) те элементы, которые попали в вычеркнутые строки. Во 2-ом столбце (с одной переменной) положим , при этом остальные элементы строк 1, 2, 5, 6, где стоит элемент , положим равными нулю. В строке 3 положим элемент x₁x₃=1.

Следовательно, получим МДНФ данной функции в виде:

f(x₁,x₂,x₃) _МДНФ= x₂˅x₁x_3.

Сравнив результаты, полученные с помощью геометрического метода, метода неопределенных коэффициентов и метода минимизирующих карт, убедились, что все ответы одинаковы, из чего можно сделать вывод, что задача решена правильно.

4. Метод Квайна.

.

Поместим члены в 1-й столбец таблицы, занумеруем их. Применим закон склеивания, результат запишем во 2-й столбец таблицы, снова занумеруем их, склеенные члены 1-го столбца отметим звездочками.

	Члены f(x1,x2,x3)	Результаты 1-го склеивания	Результаты 2-го склеивания
1.	x1x2x3 *	x1x2 (1,2) *	x2 (1,5)
2.	x1x2x3 *	x2x3 (1,4) *	x2 (2,3)
3.	x1x2x3 *	x2x3 (2,5) *
4.	x1x2x3 *	x1x3 (3,5)
5.	x1x2x3 *	x1x2 (4,5) *

Несклеившиеся простые импликанты обведем рамочкой. Дизъюнкция их дает сокращенную ДНФ, но в данном случаем сразу получаем искомый результат: f(x₁,x₂,x₃) _МДНФ= x₂˅x₁x_3.

5. Метод Квайна-Мак-Класки.

.

Заменим исходные импликанты их кодами в двоичных переменных:

010, 011, 101, 110, 111.

Разобьем коды исходных импликант на группы, поместим их в таблицу. Далее применим закон склеивания к членам соседних групп, перебирая каждый член 1-й группы со всеми членами 2-й группы и т.д.

Сделаем все это сразу в таблице:

Данная функция			Результаты 1-го склеивания			Результаты 2-го склеивания
Коды	группы		Коды	группы		Коды	группы
010 011 101 110 111	0-я	-	01- -10 -11 1-1 11-	1-я	-10 -11	-1- 1-1 -1-
	1-я	010		2-я	1-1
	2-я	011 101 110		3-я	01- 11-
	3-я	111

Далее построим таблицу меток, впишем в нее исходные и первичные импликанты в виде двоичных кодов.

	010	011	101	110	111
-1-	˅	˅		˅	˅
1-1			˅		˅

Получаем окончательный ответ: f(x₁,x₂,x₃) _МДНФ= x₂˅x₁x_3.

6. Метод карт Карно.

.

С

x₃

x₂

троим карту с симметричным расположением аргументов, один из них расположим с одной стороны, два других – с другой. Каждая клетка карты соответствует членам СДНФ функции, содержащим 3 знака.

x1x2x3 0	x1x2x3 0	1	1
x1x2x3 0 x1	1	1	1

Получаем окончательный ответ: f(x₁,x₂,x₃) _МДНФ= x₂˅x₁x_3.

Сравнив, все результаты, полученные разными методами, убедившись, что они все одинаковы, запишем ответ задачи.

Ответ: f(x₁,x₂,x₃) _МДНФ= x₂˅x₁x_3.

Задача №2. Записать формулу функции и минимизировать ее методами Квайна, Квайна-Мак-Класки и карт Карно. Сравнить результаты.