Частный институт управления и предпринимательства

Ю. В. Минченков высшая математика Исследование функций

Учебно-методическое пособие

Минск 2007

УДК 51

ББК 22.11я73

М 62

Рекомендовано к изданию редакционно-издательским советом Частного института управления и предпринимательства

А в т о р

заведующий кафедрой высшей математики и статистики Частного института управления и предпринимательства кандидат физико-математических наук, доцент Ю. В. Минченков

Р е ц е н з е н т ы:

доцент кафедры высшей математики Белорусского государственного экономического университета кандидат физико-математических наук, доцент А. И. Астровский;

доцент кафедры высшей математики и информатики Государственного института управления и социальных технологий БГУ кандидат физико-математических наук, доцент Н. Н. Рачковский

Рассмотрено и одобрено на заседании кафедры высшей математики и статистики, протокол № 2 от 12.09.2007 г.

Минченков, Ю. В.

М 62 Высшая математика. Исследование функций: учеб.-метод. пособие / Ю. В. Минченков.– Минск: Частн. ин-т упр. и предпр., 2007.– 23 с.

Учебное пособие по дисциплине «Высшая математика» подготовлено в соответствии с рабочей программой ЧИУиП по данной дисциплине, стандартом и типовой программой Министерства образования Республики Беларусь. Оно охватывает основное содержание тем «Основные теоремы дифференциального исчисления», «Исследование функций», содержит лекции, задачи и упражнения.

Предназначено для студентов Частного института управления и предпринимательства.

УДК 51

ББК 22.11я73

© Минченков Ю. В., 2007

© Частный институт управления и предпринимательства, 2007

Лекция 1. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

План:

1. Локальные экстремумы функции.

2. Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа.

Ключевые понятия

Локальный максимум. Локальный минимум. Локальный экстремум. Монотонность функции.

1. Локальные экстремумы функции

Пусть задана функция у = f (х) на множестве Х и х₀ – внутренняя точка множества Х.

Обозначим через U(х₀) окрестность точки х₀. В точке х₀ функция f (х) имеет локальный максимум, если существует такая окрестность U(х₀) точки х₀, что для всех х из этой окрестности выполнено условие f (х)  f (х₀).

Аналогично: функция f (х) имеет в точке х₀ локальный минимум, если существует такая окрестность U(х₀) точки х₀, что для всех х из этой окрестности выполнено условие f (х)  f (х₀).

Точки локальных максимума и минимума называются точками локальных экстремумов, а значения функции в них – локальными экстремумами функции.

Пусть функция f (х) определена на отрезке [а, b] и имеет локальный экстремум на каком-то из концов этого отрезка. Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для «а» и левой для «b» полуокрестностью.

Проиллюстрируем данные выше определения:

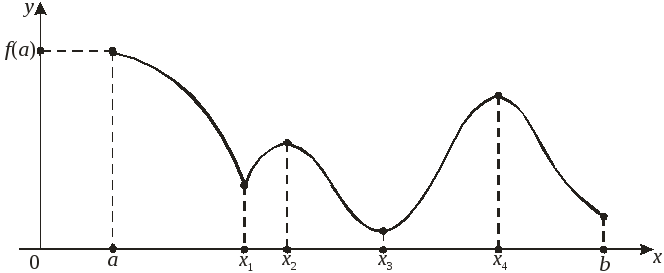
На рисунке точки х₁, х₃ – точки локального минимума, точки х₂, х₄ – точки локального максимума, х = а – краевого максимума, х = b – краевого минимума.

Заметим, что наряду с локальными минимумом и максимумом определяют так называемые глобальные минимумы и максимумы функции f(х) на отрезке [a, b]. На рисунке точка х = а – точка глобального максимума (в этой точке функция f(х) принимает наибольшее значение на отрезке [a, b]), точка х = х₃ – точка соответственно глобального минимума.