Лекции по МОТС. Автор Рызлейцев Александр.

Содержание за 2 семестр.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИГНАЛОВ РАЗЛИЧНОГО ТИПА. РАЗЛОЖЕНИЕ СИГНАЛА ПО СИСТЕМЕ ОРТОГОНАЛЬНЫХ И ОРТОНОРМАЛЬНЫХ ФУНКЦИЙ. РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ФУРЬЕ. 1

Разложение периодической функции в ряд Фурье. 3

Определение коэффициентов ряда Фурье. 5

Частный случай ряда Фурье. 6

Нахождение коэффициентов ряда Фурье от произвольной функции с симметричными пределами. 7

Частные случаи ряда Фурье. 8

Комплексная форма ряда Фурье. 11

ИНТЕГРАЛ ФУРЬЕ. 13

Частный случай интеграла Фурье. 15

Комплексная форма интеграла Фурье. 16

СПЕКТРАЛЬНЫЙ АНАЛИЗ И СИНТЕЗ ФУНКЦИИ. 17

Спектральные характеристики, зависящие от времени. 20

Свойства непрерывного спектра. (Свойства преобразований Фурье). 21

РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ЛОРАНА. 24

Свойства рядов Лорана. 26

Классификация изолированных особых точек. 26

ВЫЧЕТ ФУНКЦИИ В ОСОБОЙ ТОЧКЕ. ПРИМЕНЕНИЕ ВЫЧЕТОВ. 29

Поведение функции в окрестностях бесконечно удаленной точки. 31

Пример: 33

Применение вычетов. 33

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ. 35

Пути построения оптимальных систем. 36

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ. 38

Принцип максимума Понтрягина. 38

Метод динамического программирования. 40

Симплекс метод. 40

Лекция 1 математическое описание сигналов различного типа. Разложение сигнала по системе ортогональных и ортонормальных функций. Разложение функции в ряд фурье.

Цель. Изучить математическое описание сигналов. Рассмотреть алгоритм разложения периодической функции в ряд Фурье.

Задачи:

Изучить разложение сигналов в ряд по ортогональным и ортонормальным функциям.

Изучить разложение в ряд Фурье для периодической функции.

Изучить разложение в ряд для непериодической функции.

Изучить разложение функции на произвольном промежутке.

Функции и называются ортогональными, если интеграл от их произведения равен нулю.

Рассмотрим ряд функций: . Система функций называется ортогональной, если на отрезке от "а" до "b" все функции попарно ортогональны.

Рассмотрим промежуток где n=m:

Если система функций при n=m имеет коэффициент , то эта функция является ортонормальной. Если ортогональная система функций не ортонормальна, то ее можно получить, произведя замену:

.

Рассмотрим систему ортогональных функций и некоторой произвольной функции . Разложим функцию в ряд по системе ортогональных функций, то есть предположим, что существует разложение вида:

Определим коэффициенты ряда. Для этого умножим обе части равенства [1] на и проинтегрируем. В результате получим:

Так как система функций ортогональна и ортонормальна, то получили равенство . Выразим С_n из уравнения:

Ряд [1] называется обобщенным рядом Фурье, - коэффициентом ряда Фурье. Ряд [1] существует тогда и только тогда, когда является периодической функцией, а система функций - является равномерно сходящейся.

Разложение периодической функции в ряд Фурье.

Функция называется периодической с некоторым периодом T>0, если значение функции в точке равно значению функции в точке t:

Для периодической функции выполняется следующее равенство:

Рассмотрим гармонический процесс вида:

рисунок 1

, где

Рассмотрим функции:

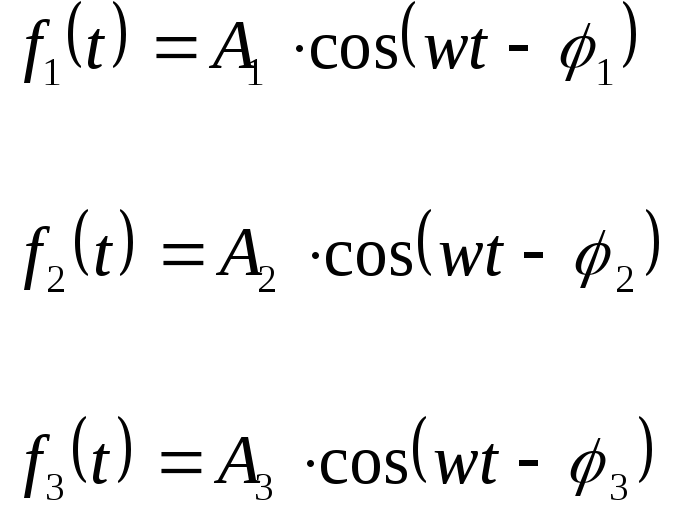
Сумма этих функций приводит к образованию некоторой новой функции с периодом Т.

.

Теорема.

Функция , представляющая собой сумму бесконечного ряда, является периодической и ее период совпадает с периодом Т первой гармоники. Частоты соседних гармоник отличаются на величину .

Доказательство.

Обозначим приращение частоты при переходе от к гармоники через , тогда для [2] получим:

.

Общий член ряда [3] называется -ой гармоникой ряда. Частота - называется частотой -ой гармоники.

Представим некоторую функцию в виде суммы гармонических функций и предположим, что существует нулевая гармоника А₀.

Распишем косинус разности:

Тогда для -ой гармоники:

Обозначим:

Тогда:

Обозначим:

Тогда [4] примет вид:

Это тригонометрическая форма ряда Фурье. Если , то . В таком случае для периодической функции с периодом ряд Фурье будет иметь следующий вид:

Определение коэффициентов ряда Фурье.

Для разложения в ряд Фурье периодических функций с периодом используется ряд ортогональных функций следующего вида:

.

Проинтегрируем [7] на промежутке .

Выразим а₀.

Определим и . Для этого [7] умножим на . В результате получим:

Так как система функций [8] ортогональна , то:

Для определения коэффициента , [7] умножим на . В результате получим:

Формулы [9], [10], [11] являются формулами для определения коэффициентов ряда Фурье. Зная их можно найти амплитуду и начальную фазу k-ой гармрмоники: