
3. Число елементів скінченного поля
Поля
 грають важливу роль в теорії скінченних
полів, оскільки кожне поле характеристики
грають важливу роль в теорії скінченних
полів, оскільки кожне поле характеристики
 повинно містити ізоморфне підполе
повинно містити ізоморфне підполе
 і
тому може розглядатися як розширення
поля
і
тому може розглядатися як розширення
поля
 .
.
Розглянемо питання про число елементів скінченного поля.
Лема
1.
Нехай
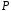 –
скінченне поле, що містить підполе
–
скінченне поле, що містить підполе
 з
з
 елементів.
Тоді
елементів.
Тоді
 складається
з
складається
з
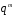 елементів, де
елементів, де
 – степінь
поля
– степінь
поля над
над
 ,
тобто розмірність векторного простору
,
тобто розмірність векторного простору
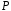 над
полем
над
полем
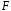 .
.
Теорема.
Нехай
 –
скінченне поле. Тоді воно складається
з
–
скінченне поле. Тоді воно складається
з
 елементів,
де
елементів,
де
 просте
число, що є характеристикою поля
просте
число, що є характеристикою поля
 ,
а
,
а
 –
натуральне число, що є степенем поля
–
натуральне число, що є степенем поля
 над його простим підполем.
над його простим підполем.
Доведення.
Оскільки
поле
 скінченне,
то його характеристика є деяке просте
число
скінченне,
то його характеристика є деяке просте
число
 .
Тому
просте підполе
.
Тому
просте підполе
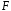 поля
поля
 ізоморфне
ізоморфне
 і,
значить, містить
і,
значить, містить
 елементів
і, отже, згідно лемі 1, поле
елементів
і, отже, згідно лемі 1, поле
 містить
містить
 елементів.
□
елементів.
□
Лема
2.
Якщо
 –
скінченне поле з
–
скінченне поле з
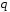 елементів,
то кожний елемент
елементів,
то кожний елемент
 задовольняє рівності
задовольняє рівності
 .
.
Означення.
Поле
 називається
полем
розкладання
многочлена
називається
полем
розкладання
многочлена
 над полем
над полем
 ,
якщо
,
якщо
 і над полем
і над полем многочлен
многочлен
 розкладається на лінійні множники.
розкладається на лінійні множники.
Лема
3.
Якщо
 –
скінченне поле з
–
скінченне поле з
 елементів
і
елементів
і
 –
підполе поля
–
підполе поля
 ,
то многочлен
,
то многочлен
 з
кільця
з
кільця
 цілком
розкладається в
цілком
розкладається в
 наступним чином:
наступним чином:
 ,
,
 ,
,
отже
 є
полем
розкладання многочлена
є
полем
розкладання многочлена
 над полем
над полем
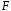 .
.
На основі представлених лем можна сформулювати головну характеризаційну теорему скінченних полів.
Теорема
(про існування і єдиність скінченних
полів).
Для кожного простого числа
 і кожного натурального числа
і кожного натурального числа
 існує скінченне поле з
існує скінченне поле з
 елементів.
Будь-яке скінченне поле з
елементів.
Будь-яке скінченне поле з
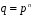 елементів ізоморфне полю розкладання
многочлена
елементів ізоморфне полю розкладання
многочлена
 над полем
над полем
 .
.
Ця
теорема дозволяє ввести в розгляд, тобто
побудувати конкретне скінченне поле
Галуа порядку
 ,
що
містить
,
що
містить
 елементів,
де
елементів,
де
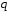 –
це степінь простого числа
–
це степінь простого числа
 ,
яке є характеристикою цього поля. Поля
цього типу позначають
,
яке є характеристикою цього поля. Поля
цього типу позначають
 або
або
 .
.
Приклад
6.
Елементами поля Галуа
 є двійкові послідовності довжиною
є двійкові послідовності довжиною
 бітів.
бітів.
Позначимо
через
 мультиплікативну групу ненульових
елементів. скінченного поля
мультиплікативну групу ненульових
елементів. скінченного поля
 .
Наступна теорема встановлює важливу
властивість такої групи.
.
Наступна теорема встановлює важливу
властивість такої групи.
Теорема.
Мультиплікативна група
 поля
поля
 циклічна.
циклічна.
Означення.
Твірний елемент циклічної групи
 називається примітивним
елементом поля
називається примітивним
елементом поля
 .
.
4. Примітивні елементи скінченного поля
Примітивним
елементом поля
 називається
такий
елемент
називається
такий
елемент
 ,
що всі ненульові елементи поля можна
зобразити у вигляді степеня елемента
,
що всі ненульові елементи поля можна
зобразити у вигляді степеня елемента
 .
.
Приклад
7.
1)
Всі ненульові
елементи
поля
 зображені у вигляді степенів елемента
зображені у вигляді степенів елемента
 .
.
2)
Примітивним елементом скінченного поля
 є 2, тому що
є 2, тому що
 ,
,
 ,
,
 ,
,
 .
.
Примітивні
елементи скінченного поля
 за простим
за простим
 розглядалися раніше в теорії чисел під
назвою первісних
коренів за модулем
розглядалися раніше в теорії чисел під
назвою первісних
коренів за модулем
 .
.
Означення.
Порядком
елемента
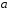 скінченного поля
скінченного поля
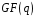 називається найменше натуральне число
називається найменше натуральне число
 з умовою
з умовою
 .
Позначається
.
Позначається
 .
.
Якщо
 – елемент порядку
– елемент порядку
 мультиплікативної групи
мультиплікативної групи
 поля
поля
 ,
то
,
то
-
 ;
; -
 є
дільником числа
є
дільником числа
 ;
; -
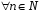
 або
або
 .
.
Зауваження.
Якщо
 – просте число, то елемент
– просте число, то елемент
 поля
поля
 можна розглядати як клас лишків кільця
можна розглядати як клас лишків кільця
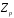 цілих чисел за простим модулем
цілих чисел за простим модулем
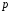 ,
представником якого є елемент
,
представником якого є елемент
 .
Тоді умова
.
Тоді умова
 рівносильна умові
рівносильна умові
 ,
через що порядок будь-якого елемента
,
через що порядок будь-якого елемента
 мультиплікативної групи
мультиплікативної групи
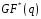 поля
поля
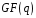 дорівнює показнику, якому належить ціле
число
дорівнює показнику, якому належить ціле
число
 за простим модулем
за простим модулем
 .
.
Приклад
8.
Визначити порядки елементів скінченого
поля
 .
.
Розв’язання.
Порядок елемента поля
 є дільником числа
є дільником числа
 ,
тобто прядки елементів містяться серед
чисел 1,2,3,6.
,
тобто прядки елементів містяться серед
чисел 1,2,3,6.
Для елемента 2:
 ,
,
 ,
,
 ,
,
отже
 .
.
Для елемента 3:
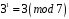 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

отже
 .
.
Для елемента 4:
 ,
,
 ,
,
 ,
,
отже
 .
.
Для елемента 5:
 ,
,
 ,
,
 ,
,
 ,
,
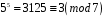 ,
,

отже
 .
.
Для елемента 6:
 ,
,
 ,
,
отже
 .
.
Для
будь-якого ненульового елемента
 порядку
порядку
 з поля
з поля
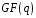 виконуються наступні твердження:
виконуються наступні твердження:
-
Якщо
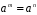 ,
то
,
то
 ,
,
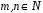 .
. -
Елементи
 поля
поля
 всі різні.
всі різні. -
Елементи
 поля
поля
 являють собою всі корені многочлена
являють собою всі корені многочлена
 .
. -
Порядок елемента
 ,
,
 ,
дорівнює
,
дорівнює
 (
( – НСД чисел
– НСД чисел
 і
і
 ).
Зокрема, якщо
).
Зокрема, якщо
 ,
то
,
то
 .
. -
Число всіх елементів поля
 ,
порядок яких збігається з порядком
,
порядок яких збігається з порядком
 елемента
елемента
 ,
дорівнює значенню функції Ейлера
,
дорівнює значенню функції Ейлера
 .
.
Важливі
властивості
мультиплікативної групи
 поля
поля
 сформулюємо у вигляді наступних теорем.
сформулюємо у вигляді наступних теорем.
Теорема.
Якщо
 – ненульові елементи поля
– ненульові елементи поля
 ,
то
,
то
 .
.
Доведення.
Нехай
 – довільний елемент мультиплікативної
групи
– довільний елемент мультиплікативної
групи
 поля
поля
 ,
,
 – порядок цього елемента. Тоді за
теоремою Лагранжа (Порядок
скінченої групи ділиться на порядок
кожної своєї підгрупи)
– порядок цього елемента. Тоді за
теоремою Лагранжа (Порядок
скінченої групи ділиться на порядок
кожної своєї підгрупи)
 ділить число
ділить число
 ,
тобто
,
тобто
 .
Отже,
.
Отже,
 і
і
 дійсно є коренем многочлена
дійсно є коренем многочлена
 .□
.□
Теорема
(про мультиплікативну групу поля
 ).
Мультиплікативна
група
).
Мультиплікативна
група
 ненульових
елементів поля
ненульових
елементів поля
 є циклічною.
є циклічною.
Доведення.
Розглянемо випадок
 .
Порядок групи
.
Порядок групи
 дорівнює
дорівнює
 .
Якщо число
.
Якщо число
 розкладено на прості множники
розкладено на прості множники
 ,
то для кожного
,
то для кожного
 ,
у полі
,
у полі
 многочлен
многочлен
 має не більше
має не більше
 коренів. А оскільки
коренів. А оскільки
 ,
то у полі
,
то у полі
 існують ненульові елементи, які не є
коренями цього многочлена. Нехай
існують ненульові елементи, які не є
коренями цього многочлена. Нехай
 – саме такий елемент поля. Покладемо
– саме такий елемент поля. Покладемо
 .
В такому разі
.
В такому разі
 ,
а тому порядок елемента
,
а тому порядок елемента
 є дільником числа
є дільником числа
 і через це має вигляд
і через це має вигляд
 ,
де
,
де
 .
З іншого боку
.
З іншого боку
 і порядок елемента
і порядок елемента
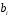 дорівнює
дорівнює
 .
.
Покажемо
тепер, що елемент
 має порядок
має порядок
 .
Припустимо супротивне. Нехай додатково
порядок елемента
.
Припустимо супротивне. Нехай додатково
порядок елемента
 – власний дільник числа
– власний дільник числа
 ,
а значить, і дільник принаймні одного
з цілих чисел
,
а значить, і дільник принаймні одного
з цілих чисел
 ,
, .
Тоді
.
Тоді
 .
.
Тепер,
якщо
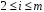 ,
то
,
то
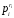 ділить число
ділить число
 .
Звідси
.
Звідси
 ,
тобто порядок елемента
,
тобто порядок елемента
 повинен ділити число
повинен ділити число
 ,
що неможливо, оскільки він дорівнює
,
що неможливо, оскільки він дорівнює
 .
.
Отже,
 – циклічна група з твірним елементом
– циклічна група з твірним елементом
 .□
.□
Теорема
(про примітивний елемент поля
 ).
В
кожному полі Галуа існує примітивний
елемент.
).
В
кожному полі Галуа існує примітивний
елемент.
Доведення.
Оскільки всі ненульові елементи поля
Галуа
 утворюють циклічну групу
утворюють циклічну групу
 ,
то серед них існує елемент порядку
,
то серед них існує елемент порядку
 ,
який є примітивним. □
,
який є примітивним. □
З
останньої теореми випливає, що примітивним
елементом поля
 є
твірний елемент
є
твірний елемент
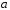 циклічної групи
циклічної групи
 .
.
