
- •Существуют и другие логические операции.
- •Логическая формула.
- •Определение логической формулы:
- •Существуют и другие логические операции.
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Предмет теории вероятностей.
- •Основные понятия теории вероятностей.
- •Элементы теории вероятностей
- •Понятие вероятности события.
- •Пример расчета вероятности
- •Понятие функции. Способы задания функции
- •Понятие функции. Способы задания функции
- •Предел функции
- •[Править] Бесконечно малая величина
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •1. Определение производной функции. Необходимое условие существования производной
- •2. Физический и геометрический смысл производной
- •1) Физический смысл производной.
- •2) Геометрический смысл производной.
2. Физический и геометрический смысл производной
1) Физический смысл производной.
Если
функция y = f(x) и ее аргумент x являются
физическими величинами, то производная![]() – скорость изменения переменной y
относительно переменной x в точке
– скорость изменения переменной y
относительно переменной x в точке![]() .
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная
.
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная![]() – скорость в момент времени
– скорость в момент времени![]() .
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то
.
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то![]() – скорость изменения количества
электричества в момент времени
– скорость изменения количества
электричества в момент времени![]() ,
т.е. сила тока в момент времени
,
т.е. сила тока в момент времени![]() .
.
2) Геометрический смысл производной.
Пусть
![]() –
некоторая кривая,
–
некоторая кривая,![]() – точка на кривой
– точка на кривой
![]() .
.
Любая
прямая, пересекающая
![]() не
менее чем в двух точках называется
секущей.
не
менее чем в двух точках называется
секущей.
Касательной
к кривой
![]() в
точке
в
точке
![]() называется
предельное положение секущей
называется
предельное положение секущей
![]() ,
если точка
,
если точка
![]() стремится
к
стремится
к
![]() ,
двигаясь по кривой.
,
двигаясь по кривой.
Из
определения очевидно, что если касательная
к кривой в точке
![]() существует,
то она единственная
существует,
то она единственная
Рассмотрим
кривую y = f(x) (т.е. график функции
y = f(x)). Пусть в точке
![]() он
имеет невертикальную касательную
он
имеет невертикальную касательную
![]() .
Ее уравнение:
.
Ее уравнение:![]() (уравнение
прямой, проходящей через точку
(уравнение
прямой, проходящей через точку![]() и
имеющую угловой коэффициент k).
и
имеющую угловой коэффициент k).
По
определению углового коэффициента
![]() ,
где
,
где![]() – угол наклона прямой
– угол наклона прямой![]() к оси
к оси
![]() .
.
Пусть![]() – угол наклона секущей
– угол наклона секущей![]() к
оси
к
оси![]() ,
где
,
где
![]() .
Так как
.
Так как
![]() –
касательная, то при
–
касательная, то при
![]()
![]() ⇒
⇒
![]() ⇒
⇒
![]() .
.
Следовательно,
.
Таким
образом, получили, что![]() –
угловой коэффициент касательной к
графику функции y = f(x) в точке
–
угловой коэффициент касательной к
графику функции y = f(x) в точке![]() (геометрический
смысл производной функции в точке).
Поэтому уравнение касательной к кривой
y = f(x) в точке
(геометрический
смысл производной функции в точке).
Поэтому уравнение касательной к кривой
y = f(x) в точке![]() можно
записать в виде
можно
записать в виде
![]()
Замечание.
Прямая, проходящая через точку![]() перпендикулярно
касательной, проведенной к кривой в
точке
перпендикулярно
касательной, проведенной к кривой в
точке![]() ,
называется нормалью к кривой в точке
,
называется нормалью к кривой в точке![]() .
Так как угловые коэффициенты
перпендикулярных прямых связаны
соотношением
.
Так как угловые коэффициенты
перпендикулярных прямых связаны
соотношением![]() ,
то уравнение нормали к кривой y = f(x) в
точке
,
то уравнение нормали к кривой y = f(x) в
точке
![]() будет
иметь вид
будет
иметь вид
![]() ,
если
,
если
![]() .
.
Если
же![]() ,
то касательная к кривой y = f(x) в точке
,
то касательная к кривой y = f(x) в точке![]() будет
иметь вид
будет
иметь вид
![]() ,
а нормаль
,
а нормаль![]() .
.
20. Основные правила дифференцирования. Дифференцирование элементарных функций.
Ключевые слова: функция, производная, правила нахождения производной, сложная функция
Производная — основное понятие дифференциального исчесления, характеризующее скорость изменения функции.
Производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.
Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференцированием.
Основные правила дифференцирования:
-
Если функция константа, т.е. y = C, где C - число, то (С)
 =0 .
=0 . -
Если функции u и v дифференцируемы в точке x, то (v+u)
 =v
=v +u
+u .
. -
Если функция Cu , где C - постоянная, дифференцируема в точке x, то (Сu)
 =Сu
=Сu .
. -
Если функции u и v дифференцируемы в точке x, то (u
 v)
v) =u
=u
 v+u
v+u v
v .
. -
Если функции u и v дифференцируемы в точке x и v(x)
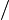 =0,
то (vu)
=0,
то (vu) =v2u
=v2u
 v−u
v−u v
v .
.
Дифференцирование сложной функции.
Рассмотрим функцию y = sin x2. Чтобы найти значение этой функции в фиксированнной точке x нужно: 1) вычислить x2; 2) найти значение синуса от полученного значения x2. Иными словами, сначала надо найти значение g(x) = x2, а потом найти sin g(x). В подобных случаях говорят, что задана сложная функция y = f(g(x)). В нашем примере u = g(x) = x2, а y = f(u) = sin u.
Пусть
y
= f(g(x))
- сложная функция, причем функция u
= g(x)
дифференцируема в точке x
,
а функция
y = f(u)
дифференцируема в соответствующей
точке u.
Тогда
функция y
= f(g(x))
дифференцируема в точке x,
причем
y![]() =f
=f![]() (g(x))
(g(x))![]() g
g![]() (x).
Запись
f'(g(x))
означает, что производная вычисляется
по формуле для f'(x),
но вместо x
подставляется
g(x).
(x).
Запись
f'(g(x))
означает, что производная вычисляется
по формуле для f'(x),
но вместо x
подставляется
g(x).
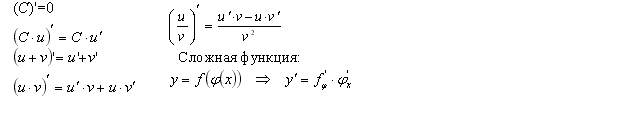
21. Приложения производной (на примере).
Применение производной в физике
В физике производная применяется в основном для вычисления наибольших или
наименьших значений для каких-либо величин.
Применение производной в алгебре
9.1. Применение производной к доказательству неравенств.
Одно из простейших применений производной к доказательству неравенств
основано на связи между возрастанием и убыванием функции на промежутке и
знаком ее производной.
Применение производной в доказательстве тождеств.
Доказательства тождества можно достигнуть иногда, если воспользоваться
одним очевидным замечанием:
Если на некотором интервале функция тождественно равна постоянной, то ее
производная на этом интервале постоянно равна нулю:
Применение производной для упрощения алгебраических и
тригонометрических выражений.
Прием использования производной для преобразования алгебраических и
тригонометрических выражений основан на том, производная иногда имеет
значительно более простой вид, чем исходная функция, благодаря чему, она
легко интегрируется, что и позволяет найти искомое преобразование исходного
выражения:
(надо спросить у кого-нибудь пример!!!!!!)
22. Интегралы и их приложения.
Интегральное
исчисление, раздел математики, в
котором изучаются свойства и способы
вычисления интегралов и их приложения.
Интегральное исчисление тесно
связано с дифференциальным
исчислением и составляет вместе с
ним одну из основных частей математического
анализа (или анализа бесконечно малых).
Центральными понятиями Интегральное
исчисление являются понятия
определённого интеграла и неопределённого
интеграла функций одного действительного
переменного.
Определённый
интеграл. Пусть требуется вычислить
площадь S
«криволинейной трапеции» — фигуры ABCD
(см. рис.), ограниченной дугой
непрерывной линии, уравнение которой
у = f (x), отрезком AB оси
абсцисс и двумя ординатами AD и BC.
Для вычисления площади S
этой криволинейной трапеции основание
AB (отрезок [a, b]) разбивают
на n участков (необязательно равных)
точками а = x0 < x1
< ... < xn-1 < < xn =
b, обозначая длины этих участков
Dx1, Dx2, ..., Dxn;
на каждом таком участке строят
прямоугольники с высотами f (x1),
f (x2), ..., f (xn) где xk
— некоторая точка из отрезка [xk
- 1, xk] (на рис.
заштрихован прямоугольник,
построенный на k-м участке разбиения; f
(xk) — его высота). Сумма Sn
площадей построенных прямоугольников
рассматривается в качестве приближения
к площади S
криволинейной трапеции:
S
» Sn
= f (x1) Dx1 + f (x2)
Dx2 + f (xn) Dxn
или,
применяя для сокращения записи символ
суммы S (греческая
буква «сигма»):
![]() Указанное
выражение для площади криволинейной
трапеции тем точнее, чем меньше длины
Dxk участков разбиения. Для
нахождения точного значения площади S
надо найти предел
сумм Sn
в предположении, что число точек
деления неограниченно увеличивается
и наибольшая из длин Dxk
стремится к нулю.
Отвлекаясь от
геометрического содержания рассмотренной
задачи, приходят к понятию определённого
интеграла от функции f (x),
непрерывной на отрезке [а, b], как к
пределу интегральных сумм Sn
при том же предельном переходе. Этот
интеграл обозначается
Указанное
выражение для площади криволинейной
трапеции тем точнее, чем меньше длины
Dxk участков разбиения. Для
нахождения точного значения площади S
надо найти предел
сумм Sn
в предположении, что число точек
деления неограниченно увеличивается
и наибольшая из длин Dxk
стремится к нулю.
Отвлекаясь от
геометрического содержания рассмотренной
задачи, приходят к понятию определённого
интеграла от функции f (x),
непрерывной на отрезке [а, b], как к
пределу интегральных сумм Sn
при том же предельном переходе. Этот
интеграл обозначается
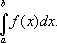 Символ
ò (удлинённое S
— первая буква слова Summa) называется
знаком интеграла, f (x) —
подинтегральной функцией, числа а
и b называются нижним и верхним
пределами определённого интеграла.
Если а = b, то, по определению,
полагают
Символ
ò (удлинённое S
— первая буква слова Summa) называется
знаком интеграла, f (x) —
подинтегральной функцией, числа а
и b называются нижним и верхним
пределами определённого интеграла.
Если а = b, то, по определению,
полагают
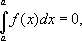 кроме
того,
кроме
того,
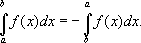 Свойства определённого интеграла:
Свойства определённого интеграла:
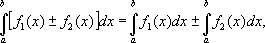
 (k
— постоянная). Очевидно также,
что
(k
— постоянная). Очевидно также,
что
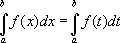 (численное
значение определённого интеграла не
зависит от выбора обозначения переменной
интегрирования).
К вычислению
определённых интегралов сводятся задачи
об измерении площадей, ограниченных
кривыми (задачи «нахождения квадратур»),
длин дуг кривых («спрямление кривых»),
площадей поверхностей тел, объёмов тел
(«нахождение кубатур»), а также задачи
определения координат центров тяжести,
моментов инерции, пути тела по известной
скорости движения, работы, производимой
силой, и многие другие задачи естествознания
и техники. Например, длина дуги плоской
кривой, заданной уравнением у = f
(x) на отрезке [a, b], выражается
интегралом
(численное
значение определённого интеграла не
зависит от выбора обозначения переменной
интегрирования).
К вычислению
определённых интегралов сводятся задачи
об измерении площадей, ограниченных
кривыми (задачи «нахождения квадратур»),
длин дуг кривых («спрямление кривых»),
площадей поверхностей тел, объёмов тел
(«нахождение кубатур»), а также задачи
определения координат центров тяжести,
моментов инерции, пути тела по известной
скорости движения, работы, производимой
силой, и многие другие задачи естествознания
и техники. Например, длина дуги плоской
кривой, заданной уравнением у = f
(x) на отрезке [a, b], выражается
интегралом
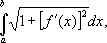 объём
тела, образованного вращением этой дуги
вокруг оси Ox,— интегралом
объём
тела, образованного вращением этой дуги
вокруг оси Ox,— интегралом
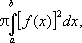 поверхность
этого тела — интегралом
поверхность
этого тела — интегралом
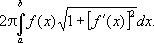 Фактическое вычисление определённых
интегралов осуществляется различными
способами. В отдельных случаях определённый
интеграл можно найти, непосредственно
вычисляя предел соответствующей
интегральной суммы. Однако большей
частью такой переход к пределу
затруднителен. Некоторые определённые
интегралы удаётся вычислять с помощью
предварительного отыскания неопределённых
интегралов (см. ниже). Как правило же,
приходится прибегать к приближённому
вычислению определённых интегралов,
применяя различные квадратурные
формулы (например, трапеций
формулу, Симпсона
формулу). Такое приближённое
вычисление может быть осуществлено на
ЭВМ с абсолютной погрешностью, не
превышающей любого заданного малого
положительного числа. В случаях, не
требующих большой точности, для
приближённого вычисления определённых
интегралов применяют графические методы
(см. Графические
вычисления).
Понятие
определённого интеграла распространяется
на случай неограниченного промежутка
интегрирования, а также на некоторые
классы неограниченных функций. Такие
обобщения называются несобственными
интегралами.
Выражения вида
Фактическое вычисление определённых
интегралов осуществляется различными
способами. В отдельных случаях определённый
интеграл можно найти, непосредственно
вычисляя предел соответствующей
интегральной суммы. Однако большей
частью такой переход к пределу
затруднителен. Некоторые определённые
интегралы удаётся вычислять с помощью
предварительного отыскания неопределённых
интегралов (см. ниже). Как правило же,
приходится прибегать к приближённому
вычислению определённых интегралов,
применяя различные квадратурные
формулы (например, трапеций
формулу, Симпсона
формулу). Такое приближённое
вычисление может быть осуществлено на
ЭВМ с абсолютной погрешностью, не
превышающей любого заданного малого
положительного числа. В случаях, не
требующих большой точности, для
приближённого вычисления определённых
интегралов применяют графические методы
(см. Графические
вычисления).
Понятие
определённого интеграла распространяется
на случай неограниченного промежутка
интегрирования, а также на некоторые
классы неограниченных функций. Такие
обобщения называются несобственными
интегралами.
Выражения вида
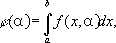 где
функция f(x, a) непрерывна по x
называются интегралами, зависящими от
параметра. Они служат основным средством
изучения многих специальных
функций (см., например, Гамма-функция).
Неопределённый интеграл. Нахождение
неопределённых интегралов, или
интегрирование, есть операция, обратная
дифференцированию. При дифференцировании
данной функции ищется её производная.
При интегрировании, наоборот, ищется
первообразная (или примитивная) функция
— такая функция, производная которой
равна данной функции. Таким образом,
функция F (x)
является первообразной для данной
функции f (x), если F"(x)
= f (x) или, что то же самое, dF (x) =
f (x) dx. Данная функция f (x)
может иметь различные первообразные,
но все они отличаются друг от друга
только постоянными слагаемыми. Поэтому
все первообразные для f (x)
содержатся в выражении F
(x) + С, которое называют
неопределённым интегралом от функции
f (x) и записывают
где
функция f(x, a) непрерывна по x
называются интегралами, зависящими от
параметра. Они служат основным средством
изучения многих специальных
функций (см., например, Гамма-функция).
Неопределённый интеграл. Нахождение
неопределённых интегралов, или
интегрирование, есть операция, обратная
дифференцированию. При дифференцировании
данной функции ищется её производная.
При интегрировании, наоборот, ищется
первообразная (или примитивная) функция
— такая функция, производная которой
равна данной функции. Таким образом,
функция F (x)
является первообразной для данной
функции f (x), если F"(x)
= f (x) или, что то же самое, dF (x) =
f (x) dx. Данная функция f (x)
может иметь различные первообразные,
но все они отличаются друг от друга
только постоянными слагаемыми. Поэтому
все первообразные для f (x)
содержатся в выражении F
(x) + С, которое называют
неопределённым интегралом от функции
f (x) и записывают
![]() Определённый интеграл как функция
верхнего предела интегрирования
Определённый интеграл как функция
верхнего предела интегрирования
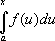 («интеграл
с переменным верхним пределом»), есть
одна из первообразных подинтегральной
функции. Это позволяет установить
основную формулу Интегральное
исчисление (формулу Ньютона —
Лейбница):
(«интеграл
с переменным верхним пределом»), есть
одна из первообразных подинтегральной
функции. Это позволяет установить
основную формулу Интегральное
исчисление (формулу Ньютона —
Лейбница):
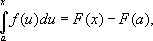 выражающую
численное значение определённого
интеграла в виде разности значений
какой-либо первообразной подинтегральной
функции при верхнем и нижнем пределах
интегрирования.
Взаимно обратный
характер операций интегрирования и
дифференцирования выражается
равенствами
выражающую
численное значение определённого
интеграла в виде разности значений
какой-либо первообразной подинтегральной
функции при верхнем и нижнем пределах
интегрирования.
Взаимно обратный
характер операций интегрирования и
дифференцирования выражается
равенствами
![]() Отсюда следует возможность получения
из формул и правил дифференцирования
соответствующих формул и правил
интегрирования (см. табл., где C,
m, a, k — постоянные и m ¹
—1, а > 0).
Отсюда следует возможность получения
из формул и правил дифференцирования
соответствующих формул и правил
интегрирования (см. табл., где C,
m, a, k — постоянные и m ¹
—1, а > 0).
Таблица основных
интегралов и правил интегрирования<
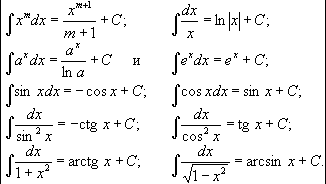 ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾
¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾
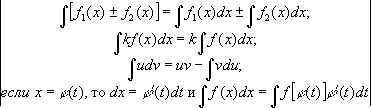 ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾
Трудность Интегральное исчисление
по сравнению с дифференциальным
исчислением заключается в том, что
интегралы от элементарных функций не
всегда выражаются через элементарные,
могут не выражаться, как говорят, «в
конечном виде». Интегральное исчисление
располагает лишь отдельными приёмами
интегрирования в конечном виде, область
применения каждого из которых ограничена
(способы интегрирования излагаются в
учебниках математического анализа:
обширные таблицы интегралов приводятся
во многих справочниках).
К классу
функций, интегралы от которых всегда
выражаются в элементарных функциях,
принадлежит множество всех рациональных
функций
¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾
Трудность Интегральное исчисление
по сравнению с дифференциальным
исчислением заключается в том, что
интегралы от элементарных функций не
всегда выражаются через элементарные,
могут не выражаться, как говорят, «в
конечном виде». Интегральное исчисление
располагает лишь отдельными приёмами
интегрирования в конечном виде, область
применения каждого из которых ограничена
(способы интегрирования излагаются в
учебниках математического анализа:
обширные таблицы интегралов приводятся
во многих справочниках).
К классу
функций, интегралы от которых всегда
выражаются в элементарных функциях,
принадлежит множество всех рациональных
функций
![]() где
P(x) и Q(x)
— многочлены. Многие функции, не
являющиеся рациональными, также
интегрируются в конечном виде, например
функции, рационально зависящие от
где
P(x) и Q(x)
— многочлены. Многие функции, не
являющиеся рациональными, также
интегрируются в конечном виде, например
функции, рационально зависящие от
![]() или
же от x и рациональных степеней
дроби
или
же от x и рациональных степеней
дроби
![]() В
конечном виде интегрируются и многие
трансцендентные функции, например
рациональные функции синуса и косинуса.
Функции, которые изображаются
неопределёнными интегралами, не
берущимися в конечном виде, представляют
собой новые трансцендентные функции.
Многие из них хорошо изучены (см.,
например, Интегральный
логарифм, Интегральный
синус и интегральный косинус,
Интегральная
показательная функция).
Понятие интеграла распространяется на
функции многих действительных переменных
(см. Кратный
интеграл, Криволинейный
интеграл, Поверхностный
интеграл), а также на функции
комплексного переменного (см. Аналитические
функции) и вектор-функции (см.
Векторное
исчисление).
О расширении
и обобщении понятия интеграла см. ст.
Интеграл.
Историческая справка. Возникновение
задач Интегральное исчисление
связано с нахождением площадей и объёмов.
Ряд задач такого рода был решен
математиками Древней Греции. Античная
математика предвосхитила идеи Интегральное
исчисление в значительно большей
степени, чем дифференциального исчисления.
Большую роль при решении таких задач
играл исчерпывания
метод, созданный Евдоксом
Книдским и широко применявшийся
Архимедом.
Однако Архимед не выделил общего
содержания интеграционных приёмов и
понятия об интеграле, а тем более не
создал алгоритма Интегральное
исчисление Учёные Среднего и Ближнего
Востока в 9—15 вв. изучали и переводили
труды Архимеда на общедоступный в их
среде арабский язык, но существенно
новых результатов в Интегральное
исчисление они не получили. Деятельность
европейских учёных в это время была ещё
более скромной. Лишь в 16 и 17 вв. развитие
естественных наук поставило перед
математикой Европы ряд новых задач, в
частности задачи на нахождения квадратур,
кубатур и определение центров тяжести.
Труды Архимеда, впервые изданные в 1544
(на латинском и греческом языках), стали
привлекать широкое внимание, и их
изучение явилось одним из важнейших
отправных пунктов дальнейшего развития
И. и. Античный «неделимых»
метод был возрожден И. Кеплером.
В более общей форме идеи этого метода
были развиты Б. Кавальери,
Э. Торричелли,
Дж. Валлисом,
Б. Паскалем.
Методом «неделимых» был решен ряд
геометрических и механических задач.
К этому же времени относятся опубликованные
позднее работы П. Ферма
по квадрированию парабол n-й степени,
а затем — работы Х. Гюйгенса
по спрямлению кривых.
В итоге
этих исследований выявилась общность
приёмов интегрирования при решении
внешне несходных задач геометрии и
механики, приводившихся к квадратурам
как к геометрическому эквиваленту
определённого интеграла. Заключительным
звеном в цепи открытий этого периода
было установление взаимно обратной
связи между задачами на проведение
касательной и на квадратуры, т. е. между
дифференцированием и интегрированием.
Основные понятия и алгоритм Интегральное
исчисление были созданы независимо
друг от друга И. Ньютоном
и Г. Лейбницем.
Последнему принадлежит термин
«интегральное исчисление» и обозначение
интеграла òydx.
При этом
в работах Ньютона основную роль играло
понятие неопределённого интеграла
(флюенты, см. Флюксий
исчисление), тогда как Лейбниц
исходил из понятия определённого
интеграла. Дальнейшее развитие
Интегральное исчисление в 18 в.
связано с именами И. Бернулли
и особенно Л. Эйлера.
В начале 19 в. Интегральное исчисление
вместе с дифференциальным исчислением
было перестроено О. Коши
на основе теории пределов. В развитии
Интегральное исчисление в 19 в.
приняли участие русские математики М.
В. Остроградский,
В. Я. Буняковский,
П. Л. Чебышев.
В конце 19 — начале 20 вв. развитие теории
множеств и теории функций действительного
переменного привело к углублению и
обобщению основных понятий Интегральное
исчисление (Б. Риман,
А. Лебег
и др.).
В
конечном виде интегрируются и многие
трансцендентные функции, например
рациональные функции синуса и косинуса.
Функции, которые изображаются
неопределёнными интегралами, не
берущимися в конечном виде, представляют
собой новые трансцендентные функции.
Многие из них хорошо изучены (см.,
например, Интегральный
логарифм, Интегральный
синус и интегральный косинус,
Интегральная
показательная функция).
Понятие интеграла распространяется на
функции многих действительных переменных
(см. Кратный
интеграл, Криволинейный
интеграл, Поверхностный
интеграл), а также на функции
комплексного переменного (см. Аналитические
функции) и вектор-функции (см.
Векторное
исчисление).
О расширении
и обобщении понятия интеграла см. ст.
Интеграл.
Историческая справка. Возникновение
задач Интегральное исчисление
связано с нахождением площадей и объёмов.
Ряд задач такого рода был решен
математиками Древней Греции. Античная
математика предвосхитила идеи Интегральное
исчисление в значительно большей
степени, чем дифференциального исчисления.
Большую роль при решении таких задач
играл исчерпывания
метод, созданный Евдоксом
Книдским и широко применявшийся
Архимедом.
Однако Архимед не выделил общего
содержания интеграционных приёмов и
понятия об интеграле, а тем более не
создал алгоритма Интегральное
исчисление Учёные Среднего и Ближнего
Востока в 9—15 вв. изучали и переводили
труды Архимеда на общедоступный в их
среде арабский язык, но существенно
новых результатов в Интегральное
исчисление они не получили. Деятельность
европейских учёных в это время была ещё
более скромной. Лишь в 16 и 17 вв. развитие
естественных наук поставило перед
математикой Европы ряд новых задач, в
частности задачи на нахождения квадратур,
кубатур и определение центров тяжести.
Труды Архимеда, впервые изданные в 1544
(на латинском и греческом языках), стали
привлекать широкое внимание, и их
изучение явилось одним из важнейших
отправных пунктов дальнейшего развития
И. и. Античный «неделимых»
метод был возрожден И. Кеплером.
В более общей форме идеи этого метода
были развиты Б. Кавальери,
Э. Торричелли,
Дж. Валлисом,
Б. Паскалем.
Методом «неделимых» был решен ряд
геометрических и механических задач.
К этому же времени относятся опубликованные
позднее работы П. Ферма
по квадрированию парабол n-й степени,
а затем — работы Х. Гюйгенса
по спрямлению кривых.
В итоге
этих исследований выявилась общность
приёмов интегрирования при решении
внешне несходных задач геометрии и
механики, приводившихся к квадратурам
как к геометрическому эквиваленту
определённого интеграла. Заключительным
звеном в цепи открытий этого периода
было установление взаимно обратной
связи между задачами на проведение
касательной и на квадратуры, т. е. между
дифференцированием и интегрированием.
Основные понятия и алгоритм Интегральное
исчисление были созданы независимо
друг от друга И. Ньютоном
и Г. Лейбницем.
Последнему принадлежит термин
«интегральное исчисление» и обозначение
интеграла òydx.
При этом
в работах Ньютона основную роль играло
понятие неопределённого интеграла
(флюенты, см. Флюксий
исчисление), тогда как Лейбниц
исходил из понятия определённого
интеграла. Дальнейшее развитие
Интегральное исчисление в 18 в.
связано с именами И. Бернулли
и особенно Л. Эйлера.
В начале 19 в. Интегральное исчисление
вместе с дифференциальным исчислением
было перестроено О. Коши
на основе теории пределов. В развитии
Интегральное исчисление в 19 в.
приняли участие русские математики М.
В. Остроградский,
В. Я. Буняковский,
П. Л. Чебышев.
В конце 19 — начале 20 вв. развитие теории
множеств и теории функций действительного
переменного привело к углублению и
обобщению основных понятий Интегральное
исчисление (Б. Риман,
А. Лебег
и др.).
