Глава 3 Электромагнитные волны в однородных изотропных средах

3.1. Плоская волна, как частный случай сферической (цилиндрической) волны. Структура поля и основные параметры

3.1.1.Плоская волна, как частный случай сферической (цилиндрической) волны

Ранее, в разделе об элементарном электрическом излучателе, было показано, что в области, достаточно удаленной от излучателя (r>>λ), поле имеет волновой характер. При этом поверхности равных фаз представляют собой сферы. Если радиус сферы достаточно велик, небольшую часть сферической поверхности можно считать плоской и волну в этой области рассматривать как плоскую [1-6, 9-12].

Плоской электромагнитной волной называется волна, у которой поверхность равных фаз представляет собой плоскость.

Подобным образом можно рассматривать и цилиндрическую волну, то есть на значительном удалении от источника поля небольшую поверхность можно также рассматривать как поверхность плоской волны. Такое упрощение поиска решений электродинамических задач позволяет значительно ускорить их решение и понять физические особенности поведения поля в волновой зоне.

Плоская волна называется однородной, если векторы поля Е и Н при соответвующем выборе направления осей координат зависят только от одной пространственной координаты и времени.

Следовательно, во всех точках равнофазной плоскости в один и тот же момент величина вектора Е (вектора Н) одинакова. Если зависимость векторов поля от времени синусоидальная (или косинусоидальная), то волна называется монохроматической или гармонической.

3.1.2. Уравнения плоской электромагнитной волны Плоские электромагнитные волны не могут быть созданы реальными источниками. Эти волны позволяют сравнительно просто установить закономерности их распространения. Существует два пути обоснования уравнений плоской волны.

Первый путь. Пусть электромагнитное поле, возбуждаемое в дальней зоне элементарным электрическим излучателем, распространяется в безграничной, однородной и изотропной среде. Поле в точке М(хуz) на расстоянии r >>λ на основании выражений (2.30) определится в виде Е₀ и Н₀

I l к ²

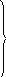Е₀ = Е_θ = j ――― sinθ е ^{–j кr};

4πωε r

(3.1)

I l к

Н₀ = Н_φ = j ――― sinθ е ^{–j кr}.

4 πr

На рисунке 3.1 источник поля размещен в точке О. При этом поле

х

S

Е₀

V

О

Н₀ М z

у

r l _z

Рис.3.1

в точке М определено выражениями (3.1), как Е₀ и Н₀ на расстоянии r. Точка М располагается на сферической поверхности S с векторами поля Е₀ и Н₀, но требуется знать векторы поля в области объема V. Введем декартову систему координат Х,У,Z. Ось Z системы совпадает с направлением радиус- вектора,

соединяющего источник О с точкой М, принятой за начало координат. К сферической поверхности прилегает область V, в пределах которой векторы поля не изменяют амплитуды. Создать режим плоской волны в объеме и ее распространение только вдоль z возможно, если длина объема l_z очень мала. Считая, что фаза векторов поля зависит только от координаты z, уравнения плоской волны с учетом выражений (3.1) запишутся в следующем виде:

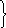Е (z) = E₀ е ^{– j кz};

H (z) = H₀ е ^{– j кz} . (3.2)

Система уравнений плоской волны (3.2) описывает поле в объеме V, причем векторы поля остаются перпендикулярными друг другу и направлению распространения. Таким образом, сферическую волну, создаваемую элементарным излучателем, в пределах области V можно рассматривать как плоскую волну.

Второй путь

Волновые уравнения для монохроматического поля, создаваемого элементарным источником, имеют вид

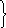▼² Е + к ² Е = 0;

▼² Н + к ² Н = 0 . (3.3)

Плоская волна распространяется только вдоль одной координаты (вдоль Z), тогда математически, используя систему (3.3), где

∂ ∂ ∂

▼ = — + — + — , (3.4)

∂ х ∂ у ∂ z

это распространение выразится в виде условия

∂ ∂ ∂

― = ― = 0; ― ≠ 0 . (3.5)

∂ х ∂ у ∂z

После подстановки условия (3.5) в систему (3.3) получается

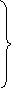∂ ² Е

—— + к² Е = 0;

∂ z ²

(3.6)

∂ ² Н

―― + к ² Н = 0.

∂ z ²

Решением полученных выражений (3.6) является решение Даламбера в виде падающей и отраженной волн

Е (z) = E₀ е ^{–j кz} + E₁ е ^{j кz} ;

H (z) = H₀ е ^{–j кz} + H₁ е ^{j кz} , (3.7)

где - Е₀ и Н₀ - есть векторы поля в точке М (рис.3.1) падающей волны;

- Е₁ и Н₁ – векторы поля в точке М отраженной волны.

Пренебрегая отраженной волной, с цель упрощения анализа поля, уравнения плоской волны примут следующий вид:

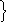Е (z) = E₀ е ^{– j кz};

H (z) = H₀ е ^{– j кz} . (3.8)

Таким образом, после сравнения выражений (3.2) и (3.8) видно, что полученные уравнения плоской волны имеют одинаковое математическое написание.

3.1.3.Структура поля плоской волны

Второе уравнение Максвелла позволяет рассмотреть структуру поля в однородной изотропной среде. Это уравнение устанавливает связь между векторами поля при отсутствии источников. Причем следует помнить, что векторы поля лежат в плоскости ХМУ (рис.3.1), поперечной к направлению распространения, то есть по оси z. Следовательно, векторы поля могут иметь проекции на ось Х или на ось У, а на ось Z проекция векторов поля равна нулю. Поэтому при распространении волны вдоль оси Z амплитуда проекций векторов изменяется. При использовании принципа перестановочной двойственности уравнение для Е и Н будет иметь вид [1-6]

rot Е = -- jωμН; rot Н = jωε Е. (3.9)

С учетом условия (3.5) структура поля описывается

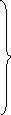
∂ Н _у ∂ Е_у

jωε Е _х = – ―― ; jωμ Н _х = ―― ;

∂ z ∂ z

∂ Н _х ∂ Е _х

jωε Е _у = – ―― ; jωμ Н _у = ——; (3.10)

∂ z ∂ z

jωε Е _z = 0; jωμ Н _z = 0.

Полученный результат позволяет установить:

- выражения (3.10) описывают поле поперечной волны или волны типа ТЕМ;

- в структуре поля отсутствуют составляющие, дающие проекцию на ось Z.

3.1.4. Параметры плоской волны

Волновое сопротивление среды

Структура поля описывается выражениями (3.10), однако каким образом связаны векторы поля в плоской волне устанавливает волновое сопротивление или характеристическое сопротивление среды, измеряемое в омах. Отношение векторов поля Е / Н = Z _в и есть волновое сопротивление среды.

Д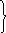ля гармонически изменяющегося поля и с векторами, совпадающими с осями Х и У, составляющие имеют вид

Е _х = Е₀ е ^{-- j(ωt – кz + ψ)};

Н _у = Н ₀ е ^{--j(ωt – кz + φ)} . (3.11)

Волновое сопротивление, равное отношению векторов в выражении (3.11)

Е ₀

Z_в = ―― е ^{j (ψ -- φ)}, (3.12)

Н ₀

представляет собой величину комплексную, не зависящую от координаты Z и времени. После дифференцирования системы (3.10) по z получаются два следующих уравнения:

E_x = Н _у√μ / ε ; Е _у = Н _х√μ / ε . (3.13)

Из сравнения выражений (3.12) и (3.13) видно, что

Е_х Е _у

Z _B = ―― = ―― = √μ _к / ε _к , (3.14)

Н _у Н _х

где - отношение амплитуд векторов равно модулю волнового сопротивления;

- волновое сопротивление среды имеет комплексную величину и зависит только от параметров среды.

Коэффициент распространения

Зависимость составляющих поля плоской волны от координаты Z устанавливается в выражениях (3.8) множителем е ^{–j кz}. В степень множителя входит коэффициент распространения к, который ранее был назван волновым числом среды. Коэффициент является величиной комплексной

к = ω √ με = ω √ (μ – j σ _м / ω) (ε – j σ / ω) = ω√ μ (ε – j σ / ω) . (3.15)

Коэффициент распространения, как комплексная величина, обычно записывается в комплексной алгебраической форме

к = β - j α , (3.16)

где - β есть коэффициент фазы, который показывает изменение фазы электромагнитной волны (или изменения положения векторов поля) на единицу длины, распространяющейся в направлении оси Z. Измеряется в радианах на метр. При этом известно, что расстояние, на котором фаза изменяется на угол равный 2π, называется длиной волны в среде, то есть

β λ = 2π ; (3.17)

- α есть коэффициент затухания, показывающий изменение амплитуды векторов поля на единицу расстояния, пройденного распространяющейся плоской волной.

Уравнения плоской волны с учетом выражения (3.16) имеют вид

Е (z) = E₀ е ^{– α z} е ^{j (ωt – β z)};

Н (z) = Н₀ е ^{– α z} е ^{j (ωt – β z)} . (3.18)

Ниже рассмотрены амплитудные изменения векторов поля (рис.3.2) при распространении плоской волны в направлении оси Z. Прежде необходимо задаться условием размещения векторов. Пусть вектор Е совпадает с осью Х, а вектор Н – с осью У. При этом амплитуда векторов по оси Z уменьшается по экспоненте, то есть амплитуда изменяется на основании закона – е ^{– α z} .

Е₀ е ^{– α z}

Е_{0 Направление распространения волны}

ψ

z

Н₀

Н₀ е ^{– α z} Е₀ е ^{– α z}

у

Рис.3.2

На рисунке 3.2 дано пространственное представление закона распределения векторов поля Е_х(z) = Е₀ е ^{–α z} и Н_у(z) = Н₀ е ^{– α z} вдоль направления распространения. Картина зафиксирована в момент t = 0 при нулевом значении начальной фазы напряженности электрического поля. В этот же момент начальная фаза напряженности магнитного поля равна ψ, которая определяет аргумент комплексного волнового сопротивления (см. выражение 3.12) среды. Проведем логарифмирование Е_х (z) с целью установления параметров коэффициента затухания α

α = ( 1 /z) ln Е₀ / Е _х(z), Нп / м . (3.19)

Выражение (3.19) показывает, что коэффициент затухания выражается в неперах на метр пройденного волной пути. Под затуханием в один непер понимается уменьшение амплитуды векторов в е раз (е = 2,718 раз).Для практических целей пользуются единицей измерения децибел на метр (дб/м), смысл которой очевиден из формулы

α = ( 1 / z) 20 lg[ Е₀ / Е _х (z)], дб / м. (3.20)

Указанные единицы измерения коэффициента затухания связаны между собой простым соотношением: 1 непер = 8,686 децибел.

Скорость распространения плоской волны

Фронт волны будет перемещаться в однородной изотропной среде с некоторым постоянным значением фазы, в частности, для электрического вектора из выражения (3.18)

Ψ = ω t - βz = 0, (3.21)

со временем в направлении оси Z со скоростью, которую принято называть фазовой скоростью ν_ф. Эта скорость может определиться путем дифференцирования выражения (3.21) по времени

ω - β ( ∂z / ∂ t) = 0, (3.22)

но ∂ z ⁄ ∂ t = ν_ф, следовательно, выражение (3.22) примет вид

ν_ф = ∂ z / ∂ t = ω / β. (3.23)

Таким образом, скорость распространения плоской волны определяется частотой ω и коэффициентом фазы β.