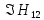5. Анализ типовых структур.

Очень часто звенья системы связаны между собой некоторыми простыми структурами, которые называются типовыми.

Все системы с типовой структурой имеют один внешний вход v и один внешний выход y, т.е. характеризуются одной переходной функцией H(p).

Рассмотрим систему из 2-х звеньев:

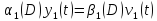
После преобразований:

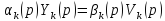
Или

Напомним, что по определению:

1. Последовательное и параллельное соединения звеньев.

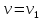
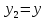
Тогда:

и находим:

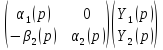
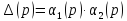выразим .

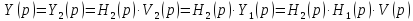
Частотная характеристика:

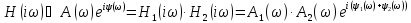
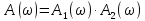
Для последнего соединении переходной функции системы равно произведению переходных функций звеньев; АЧХс равно произведению АЧХ; ФЧХс равно сумм ФЧХ.

Допустимо, что переходная функция одного из звеньев не было строго реализуемо, лишь бы таковой была переходная функции соединения. Соединение устойчиво, если устойчивы звенья.

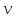
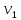
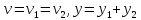
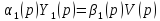
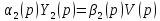
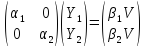
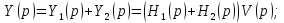
Частотная характеристика R(w)

Для параллельного соединения переходная функция равняется сумме переходных функций, МЧХс равно произведению МЧХ; ВЧХс равно сумм ВЧХ. Соединение устойчиво, если только устойчивы звенья.

При вычислении переходной функции системы возможно сокращение общих множителей в числителе и знаменателе. Вывод об устойчивости по знаменателю следует делать до этапа сокращения.

Рассмотрим обратную задачу. Пусть звено задано переходной функцией H(p). Тогда любое представление 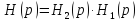или 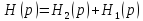можно интерпретировать как разбиение звена на 2 последовательных или параллельных соединенных. Если H(p)-строго реализуема, а значит имеет только простые корни, то

Тогда такую же переходную функцию имеет система с n звеньями и одним усилителем , если все звенья расположены параллельно т.е.

,

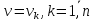v- внешний вход, y- внешний выход.

Если все 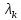, 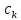- вещественны, то

………………………………

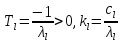
Можно тогда представить такое звено следующей структурной схемой. Которая включает тольо идеальные усилители и апериодические звенья.

2. Соединения с отрицательной обратной связью.

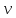
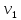
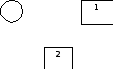
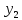
Звено 1 – стоит в прямой цепи, звено 2- стоит в обратной цепи.

Тогда согласно системе: .

В изображениях:

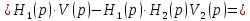
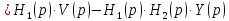
Следовательно:

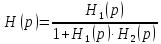
Тогда, если

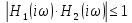
То .

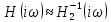Перейдем к изучению устойчивости этого соединения.

Т.к. , то

Тогда устойчивость зависит от свойств 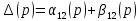, т.е. напрямую не следует из устойчивости 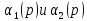(т.е. каждого звена этого соединения).

Докажем достаточное условие устойчивости в этом случае.

Теорема 1.5.1. пусть звенья 1 и 2 соединения с отрицательной обратной связью устойчивы. Пусть – является правильной дробью, а 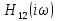для любого не является вещественным числом . Тогда характеристический многочлен - устойчив.

Доказательство: введем вспомогательную функцию:

Известно, что - устойчивый, значит, все его корни лежат в левой полуплоскости. Пусть это некие . Будем изменять k от 0 до 1, тогда каждый корень начнет двигаться по непрерывной кривой называемой корневым годографом.

Предположим, что такая кривая пересечет при каком – то 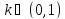мнимую ось. Но тогда:

Или

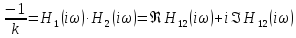
Но тогда при этом предположении .

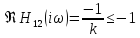Это противоречит условию теоремы.

Таким образом, доказана достаточность этих условий.

Геометрически эта теорема означает, что если построить годограф то он не должен пересекать горизонтальную ось () левее т. (-1) при .

Например:

Пример:

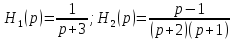
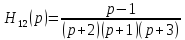
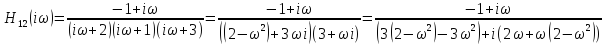
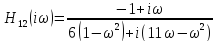
Нейдем 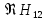и .

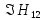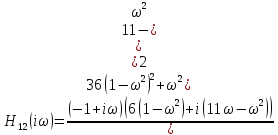
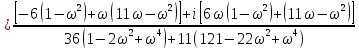
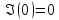точка на действительной прямой

При

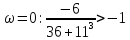
Пр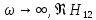и и

Нарисовать параметрическую кривую (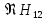,и определить устойчивость в этом случае.

Кроме этой теоремы, еще одним достаточным условием можно пользоваться!

Теорема 1.5.1’. если , где – устойчивый многочлен и выполнены все условия 1.5.1 для , а также

то характеристический многочлен 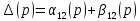- устойчив!

В этом условии – важно, что у может быть нулевой корень, что говорит о его неустойчивости. Т.е. неустойчивость такого типа – не обязательно порождает неустойчивость !

Это геометрически означает, что при 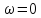кривая 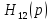может начинаться с бесконечно удаленной точки, то все равно должна при стремится к началу координат (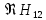,).