Лекция 4 Геометрия двухмерных кривых

Кроме пространственных линий, для нас практическое значение будут иметь двухмерные кривые на плоскости. В частности, двухмерным пространством будет служить область параметров поверхностей.

Рассмотрим случай двухмерной кривой. Пусть на плоскости определена декартова прямоугольная система координат с началом в точке О и базисными векторами е₁ и е₂. Компоненты двухмерных векторов будем обозначать через х и у. Большинство формул для двухмерных кривых можно получить из соответствующих формул для пространственных кривых, положив в них третью координату равной нулю и опустив ее и все векторы, ортогональные плоскости кривой (в их числе бинормаль). Радиус-вектор двухмерной кривой будет описываться выражением

(55)

Для двухмерной кривой r(s) формулы Френе-Серре имеют вид:

(56)

где t = dr/ds – касательный вектор кривой, s – длина дуги кривой. Кривизна двухмерной кривой определяется равенством:

(57)

Натуральное уравнение двухмерной кривой выражает ее кривизну как функцию дуги вдоль кривой и имеет вид:

Чтобы сохранить справедливость всех приведенных выше формул, следует переопределить операцию векторного произведения для двухмерных векторов. Результатом векторного произведения двухмерных векторов и будем считать скалярную величину, равную

(58)

Выразим через координаты х и у производную длины дуги и кривизну двухмерной кривой,

(59)

(60)

Эволюта и эвольвента. Для каждой обыкновенной точки кривой можно указать центр кривизны. Геометрическое место центров кривизны всех точек данной кривой называется эволютой этой кривой. Выражение для радиус-вектора эволюты a(t) получим, добавив к радиус-вектору кривой r(t) вектор нормали, деленный на кривизну кривой:

(61)

При произвольной параметризации кривой получим:

(62)

Для двухмерной кривой запишем векторное равенство (63) отдельно для каждой координаты эволюты :

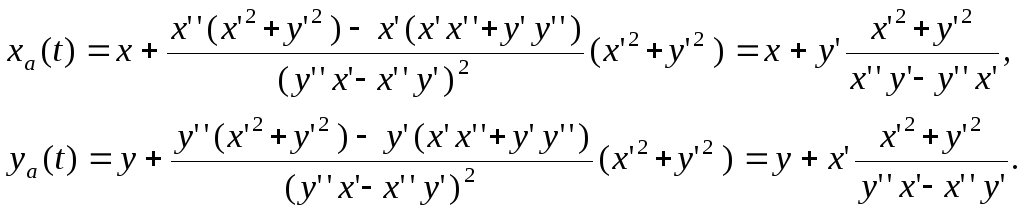(64)

В точках распрямления радиус-вектор соответствующей точки эволюты стремится к бесконечности. Если точка распрямления является точкой перегиба, то эволюта терпит в соответствующей точке разрыв. Эволюта в каждой своей точке касается нормали к исходной кривой в соответствующей точке. Эволюту можно определить как огибающую семейства нормалей.

Исходная кривая по отношению к своей эволюте является эвольвентой (разверткой). Для кривой a(s) эвольвента описывается радиус-вектором:

(65)

где s – длина дуги кривой a(s), s₀ = const, t – касательная к кривой. Для заданной плоской кривой можно построить множество эвольвент, в зависимости от s₀ (или от того, в какой точке кривой принять длину дуги равную нулю). На рис. 12 показана кривая a(s) и ее эвольвента.

Эвольвента строится следующим образом. Положим, что длина дуги кривой a(s) отсчитывается от точки С₀. Для получения точки М эвольвенты, соответствующей некоторой точке C_i исходной кривой, построим в точке C_i касательную и отложим на ней с учетом знака отрезок длиной, равной длине

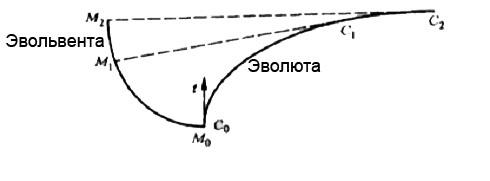
Рис. 12. Эволюта и эвольвента

дуги С_iC₀, взятой с отрицательным знаком, если значение параметра в точке С_i больше значения параметра в точке С₀, и взятой с положительным знаком в противном случае. Можно сказать, что эвольвента представляет собой развертку исходной кривой.

Для доказательства равенства (65) покажем, что эволюта кривой r(s) есть кривая a(s). Заметим, что параметр s является длиной дуги кривой a(s), но не является длиной дуги для эвольвенты r(s), поэтому радиус-вектора эволюты выразится правой частью формулы (63). Подставим в формулу эволюты (63) значения векторной функции r и ее производных, выраженные через векторную функцию а и ее производные по параметру s:

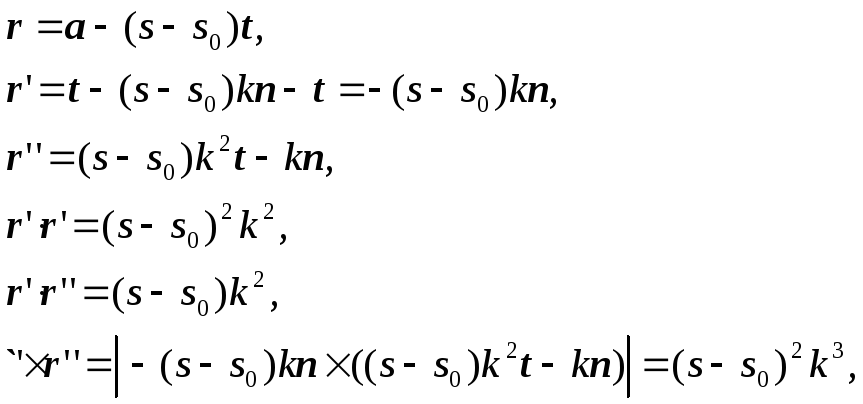
где s – длина дуги кривой a(s), k – ее кривизна, n – главная нормаль и t – касательная кривой a(s). В результате получим:

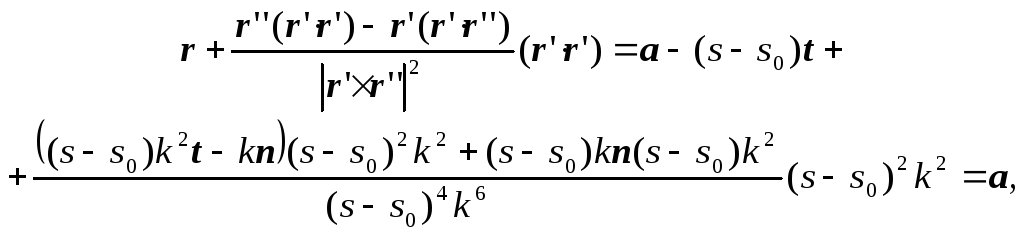
что и требовалось доказать.