6. Оценка математической модели прогнозирования

На этом этапе исследования определяются параметры различ­ных видов аппроксимирующих функций. Наиболее распространен­ными методами оценки параметров аппроксимирующих зависимо­стей являются метод наименьших квадратов (МНК) и его модифи­кации, метод экспоненциального сглаживания, метод вероятност­ного моделирования, метод адаптивного сглаживания.

Рассмотрим для примера МНК и метод экспоненциального сглаживания.

Метод наименьших квадратов состоит в определении парамет­ров модели тренда, минимизирующих ее отклонение от точек ис­ходного временного ряда:

(7.31).

где -— расчетные (теоретические) значения исходного ряда;

— фактические значения исходного ряда;

n — число наблюдений.

Классический метод наименьших квадратов предполагает рав­ноценность исходной информации в модели. В реальной же прак­тике будущее поведение процесса в большей степени определяется поздними наблюдениями, чем ранними. Речь идет о дисконтирова­нии, т. е. уменьшении ценности более ранней информации.

Дисконтирование учитывают путем введения в модель (7.31) некоторых весов β_i, < I. Тогда

Коэффициенты β_i - могут быть заданы в числовой форме или в виде функциональной зависимости таким образом, чтобы по мере продвижения в прошлое веса убывали.

Метод наименьших квадратов широко применяется при про­гнозировании, что объясняется его простотой и легкостью реализа­ции на ЭВМ. К недостаткам МНК можно отнести следующее.

Во-первых, модель тренда жестко фиксируется, и с помощью МНК можно получить прогноз на небольшой период упреждения. Поэтому МНК относят к методам краткосрочного прогнозирова­ния.

Во-вторых, значительную трудность представляет правильный выбор вида модели, а также обоснование и выбор весов во взве­шенном методе наименьших квадратов.

Наконец, МНК очень просто реализуется только для линейных и линеаризуемых зависимостей, когда для получения оценок коэф­фициентов моделей решается система линейных уравнений. Задача значительно усложняется, если для прогноза используется функци­ональная зависимость, не сводимая к линейной.

Метод экспоненциального сглаживания является эффективным и надежным методом среднесрочного прогнозирования.

Здесь следует остановиться более подробно на учете важности ретроспективной информации.

Практически большее значение для построения прогноза име­ет информация, описывающая процесс в моменты времени, стоя­щие ближе к настоящему (нулевому) моменту времени. Чем даль­ше мы углубляемся в ретроспекцию, тем менее ценной для прогно­за становится информация. Это можно учесть, придавая членам исходного динамического ряда некоторые веса, тем большие, чем ближе находится точка к началу периода прогноза.

Это положение лежит в основе метода экспоненциального сгла­живания.

Сущность метода заключается в сглаживании исходного динамического ряда взвешенной скользящей средней, веса которой (ω_i) подчиняются экспоненциальному закону.

Пусть исходный динамический ряд описывается полиномом следующего вида:

(7.32)

где,,… —коэффициенты;

р — порядок полинома;

, — случайная ошибка.

Метод экспоненциального сглаживания позволяет построить такое описание процесса (7.32), при котором более поздним на­блюдениям придаются большие веса по сравнению с ранними на­блюдениями, причем веса наблюдений убывают по экспоненте.

Выражение

(7.33)

называется экспоненциальной средней k-го порядка для ряда у_t, где α — параметр сглаживания.

В расчетах экспоненциальную среднюю определяют, пользуясь рекуррентной формулой, полученной Брауном

(7.34)

Использование соотношения(6.34) предполагает задание на­чальных условий , которые могут быть определены по формуле Брауна- Мейера:

(7.35)

где p=1,2,…, n+1.

— оценки коэффициентов.

Оценки коэффициентов прогнозирующего полинома определя­ют через экспоненциальные средние по фундаментальной теореме Брауна— Мейера. В этом случае коэффициенты находят решени­ем системы (p-1) уравнений с (p+1) неизвестными, связываю­щей параметры полинома с исходной информацией.

Рассмотрим применение метода экспоненциального сглажива­ния для двух наиболее употребительных случаев, когда тренд опи­сывается линейной функцией и параболой.

Линейная модель Брауна

(7.36)

Начальные приближения для случая линейного тренда равны (по формуле (7.35)):

экспоненциальная средняя 1-го порядка:

; (7.37)

А экспоненциальная средняя 2-го порядка:

. (7.38)

Зная начальные условия и и значение параметра α, вычисляют экспоненциальные средние 1-го и 2-го порядка:

(7.39)

(7.40)

Оценки коэффициентов линейного тренда

(7.41)

(7.42)

Прогноз на L шагов (на время ) равен: .

Ошибка прогноза

(7.43)

Параболический тренд

(7.43)

Начальные приближения

(7.45)

(7.46)

(7.47)

Экспоненциальные средние

(7.48)

(7.49)

(7.50)

Оценки коэффициентов параболической зависимости для тренда

(7.51)

(7.52)

(7.53)

Прогноз на L шагов (на время ) равен:

. (7.54)

Ошибка прогноза

(7.55)

Для метода экспоненциального сглаживания основным и наи­более трудным моментом является выбор параметра сглаживания а, начальных условий и степени прогнозирующего полинома.

Параметр сглаживания а определяет оценки коэффициентов модели, а следовательно, результаты прогноза.

В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем боль­ше а, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий убывает быстро. При малом а прогнозные оценки учитывают все наблюдения, при этом умень­шение влияния более ранней информации происходит медленно.

Для приближенной оценки а известны два основных соотно­шения:

• соотношение Брауна, выведенное из условия равенства скользя­щей и экспоненциальной средней

; (7.56)

где N — число точек ряда, для которых динамика ряда считается однород­ной и устойчивой (число точек в интервале сглаживания).

Иногда , где п - число наблюдений (точек) в ретроспективном динамическом ряду;

• соотношение Мейера

(7.57)

где — средняя квадратическая ошибка модели;

— средняя квадратическая ошибка исходного ряда.

Однако достоверно определить и из исходной информа­ции очень сложно, поэтому использование соотношения (7.57) за­труднено.

Очевидно, что выбор параметра а нужно связывать с точностью прогноза, поэтому для более обоснованного выбора а можно ис­пользовать процедуру обобщенного сглаживания.

В этом случае получаются следующие соотношения, связываю­щие дисперсию прогноза и параметр сглаживания а:

Для линейной модели

(7.58)

Для квадратичной модели

(7.59)

где

τ — период прогноза;

— средняя квадратическая ошибка аппроксимации исходного дина­мического ряда.

При a = 0 выражения, стоящие в правых частях формул (7.58), (7.59), обращаются в нуль, следовательно, для уменьшения ошибки прогноза необходимо выбирать минимальное а.

В то же время, чем меньше а, тем ниже точность определения начальных условий, а следовательно, ухудшается и качество про­гноза.

Таким образом, использование формул (7.58), (7.59) приводит к противоречию при определении параметра сглаживания. В ряде случаев параметр а выбирают так, чтобы минимизировать ошибку прогноза, рассчитанного по ретроспективной информации.

Качество прогноза во многом зависит от выбора порядка про­гнозирующего полинома. Известно, что превышение второго по­рядка модели не приводит к существенному увеличению точности прогноза, но значительно усложняет расчет.

Отметим в заключение, что метод экспоненциального сглажи­вания является одним из наиболее эффективных, надежных и ши­роко применяемых методов прогнозирования. Он позволяет полу­чить оценку параметров тренда, характеризующих не средний уро­вень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения, и при этом отличается простотой вычислительных операций.

Рассмотрим пример. Пусть задан временной ряд :

Год	2004	2005	2006	2007
T	1	2	3	4
	40	43	46	48

Можно считать, что аппроксимирующая функция (тренд) опи­сывается линейной функцией.

1. Определим коэффициенты прямой по методу на­именьших квадратов. Для этого вычислим ряд промежуточных зна­чений и их суммы. Результаты занесем в табл. 7.3.

Таблица 7.3

Расчетная таблица

Год	Период, t	Факт. Знач.	Расчётные значения
2004	1	40	1	40	40,2	0,2
2005	2	43	4	86	42,9	-0,1
2006	3	46	9	138	45,6	-0,4
2007	4	48	16	192	48,3	0,3
Итого	10	177	30	456	-	-

Далее найдем

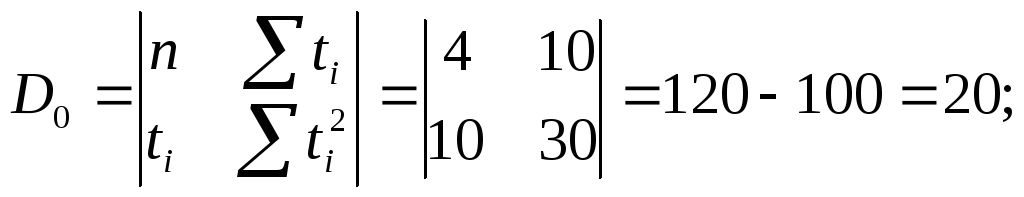
Окончательно уравнение прямой имеет вид

у = 37,5 + 2,7t.

Подставив в него значения t = 1, 2, 3, 4, получим расчетные значения тренда (табл. 6.3).

Основная ошибка

2. Параметр сглаживания

3. Начальные условия

(7.48)

4. Для t = 2 вычислим экспоненциальные средние:

значения коэффициентов:

прогнозируемые значения:

отклонения от фактического значения:

Аналогичные вычисления выполним для t = 3 (2006 г.), t = 4 (2007г.), t = 5 (2008 г.).

Результаты представим в табл. 7.4.

Таблица 7.4

Типовая таблица для построения прогноза по методу

экспоненциального сглаживания

Год	Период, t	Факт. Знач.	Расчётные значения
2004	1	40
2005	2	43	36	32	40	2,6	42,6	-0,1
2006	3	46	38,6	34,6	42,6	2,7	45,3	-0,4
2007	4	48	41,6	37,4	45,8	2,8	48,6	0,3
2008	L=1	-	44,2	40,1	48,3	2,7	51	-

Для t=3 (2006 г.):

Для t=4 (2007 г.):

Для построения модели прогноза на 2008 г. (L. = I) определим

Окончательная модель прогноза имеет вид

гдеL = 1, 2, ... (что соответствует 2008, 2009 гг., и т. д.).

Ошибка прогноза