2.2. Устойчивость динамических систем

Понятие устойчивости. На любую систему всегда действуют различные возмущения, которые могут нарушить ее нормальную работу. Хорошая система должна устойчиво функционировать при всех действующих на нее возмущениях.

В простейшем случае понятие устойчивости системы связано с ее способностью возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него возрастающие по амплитуде колебания.

Очевидно, что система с расходящимся процессом была бы неработоспособной. Следовательно, устойчивость является необходимым условием работоспособности любой системы.

На рис 3 представлены примеры графики движения устойчивых и неустойчивых систем при воздействии постоянного (ступенчатого) входного сигнала Х(t) =Const или постоянного возмущения.

Устойчивые СУ

Неустойчивые СУ

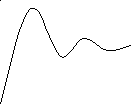
Y

Y

Экспоненциальная

неустойчивость

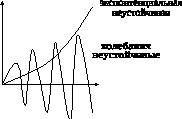
Колебательная

неустойчивость

t

t

t

Рис. 3

Устойчивость по Ляпунову. Впервые строгое определение устойчивости было дано русским ученым А.М.Ляпуновым в 1892г. Отсутствие такого определения часто приводило к недоразумениям, так как динамические системы, устойчивые в одном смысле, могут оказаться неустойчивыми при другом понимании этих слов, и наоборот. Определение устойчивости А.М.Ляпунова оказалось настолько удачным и наилучшим образом удовлетворяющим многим задачам динамики, что оно в настоящее время принято как основное.

Введем новые переменные

х(t)= Y(t) – Y^*(t)

равные разности переменных Y в возмущенном Y(t) и невозмущенном Y^*(t) движении. Под возмущенным движением мы понимаем движение системы при измененных начальных условиях.

Движение называется устойчивым по Ляпунову, если при небольших изменениях начальных значений переменных Y(t), что соответствует малым начальным возмущениям, возмущенное движение в моменты времени t>t₀ будет отличаться от невозмущенного движения сколь угодно мало.

Другими словами, невозмущенное движение называют устойчивым по отношению к переменным x, если для любого произвольно заданного числа ε>0, как бы мало оно ни было, можно подобрать другое такое число δ(ε) >0, что при всяких возмущениях x₀, удовлетворяющих условию

|x₀| ≤ δ

и при любом t ≥ t₀ будет выполняться неравенство

|х(t)| < ε.

В противном случае движение неустойчиво.

На рис.4 представлена графическая иллюстрация определения устойчивости по Ляпунову для устойчивой Y₁(t) и неустойчивой Y₂(t) систем. В устойчивой системе переходный процесс не должен выходить из трубки радиуса ε образованной вокруг невозмущенной траектории Y^*(t).

Y₂(t)

Y

Y^*(t)

Y₁(t)

x₁(t)

δ

ε

δ

ε

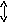
x₀₁

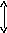
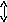
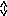
t

t₀

Рис. 4

Множество значений параметров объекта, в том числе и начальных условий, при которых исследуемый процесс устойчив, называется областью устойчивости системы.

Система (или движение) называется асимптотически устойчивой, если имеет место равенство

lim [Y(t) – Y^*(t)] = 0,

t→ ∞

т.е. возмущенное и невозмущенное движение неограниченно сближаются с течением времени.

Если движение является асимптотически устойчивым при любых отклонениях начальных условий, т.е. при любых возмущениях, то такая система называется асимптотически устойчивой в целом.

Отметим некоторые особенности определения устойчивости по А.М.Ляпунову. Во-первых, предполагается, что возмущения налагаются только на начальные условия, т.е. возмущенное движение в системе происходит при тех же силах, что и невозмущенное движение. Во-вторых, устойчивость рассматривается на бесконечно большом промежутке времени. И в-третьих, возмущения предполагаются малыми. Несмотря на эти ограничения, определение устойчивости движений систем по А.М.Ляпунову является эффективным и плодотворным в приложениях.