Тема 2. Числовые ряды.

§2.1. Основные понятия.

Пусть задана числовая последовательность (1)

Рассмотрим следующую последовательность:

Если суммы (2) при имеют предел, то этот предел считают суммой всех членов последовательности (1).

Определение 1 Последовательность (1), рассматриваемая с точки зрения существования предела при , называется числовым рядом. Обозначается: (3)

Определение 2 называется -й частичной суммой ряда (3), а называется общим членом ряда.

Если , то иначе это записывают так: (4), т.е. является суммой ряда.

Определение 3 Ряд называется сходящимся, если его сумма конечна, и расходящимся, если его сумма бесконечна или не существует.

Примеры:

1) Рассмотрим ряд

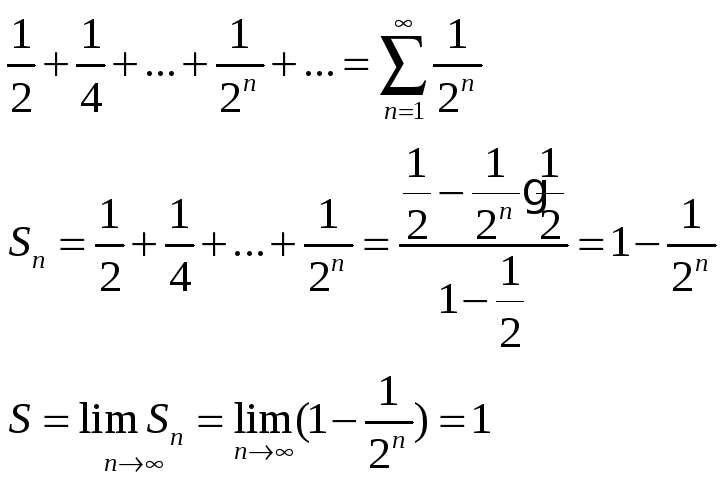
2)

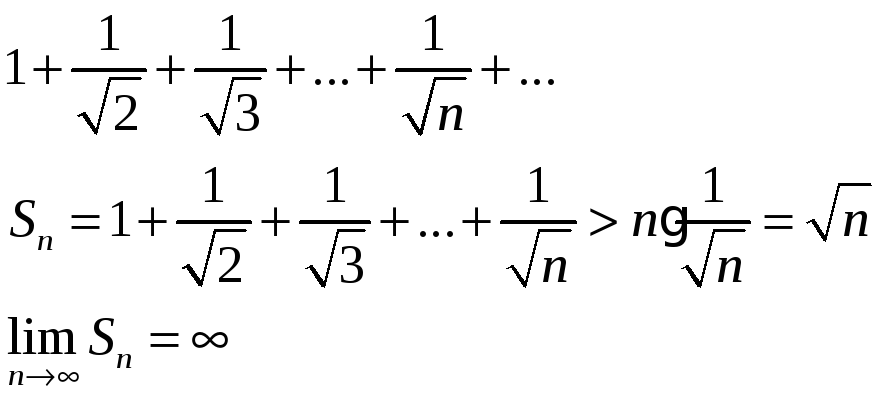
3) 1-1+1-1+1-… ряд расходится, т.к. предела нет

4)

§2.2. Простейшие свойства рядов.

Свойство 1 (Необходимый признак сходимости ряда).

Если ряд (А) сходится, то его общий член ряда стремится к нулю .

Опр. Произведением ряда (А) на число назовем ряд С(А). Суммой рядов (А) и (В) назовем ряд (С) с общим членом .

Свойство 2. Ряд, полученный умножением сходящегося ряда (А) на конечное число , тоже сходится, причем его сумма , где - сумма ряда (А).

Свойство 3. Если ряды (А) и (В) сходятся, то ряд, представляющий их сумму, тоже сходится, причем его сумма

Определение Остатком ряда (А) после -го члена (или -м остатком) назовем ряд

Свойство 4. При любом сходимость ряда (А) равносильна сходимости его -го остатка, причем сумма ряда (А) .

Следствие из свойства 4: выбрасывание из ряда конечного числа его членов или вписывание в него конечного числа членов не влияет на сходимость ряда. При этих действиях достаточно далекие остатки нового ряда могут являться остатками прежнего ряда, и т.к. прежний ряд сходится, то новый тоже будет сходиться.

§2.3. Критерий Больцано-Коши сходимости ряда.

Рассмотрим ряд (А). Сходимость ряда по определению равносильна тому, что последовательность его частичных сумм сходится (т.е. имеет кон.предел).

Пусть последовательность частичных сумм сходится. Сходимость последовательности означает, что для (критерий Больцано-Коши для последовательности).

Пусть . Тогда , т.е. получим отрезок ряда меньше любого .

Теорема (критерий Больцано-Коши). Для того, чтобы ряд (А) сходился необходимо и достаточно, чтобы для , т.е. чтобы достаточно далекие отрезки ряда становились по модулю как угодно малыми.

Пример:

Рассмотрим гармоничный ряд

Средним гармонических чисел называют такое число , что

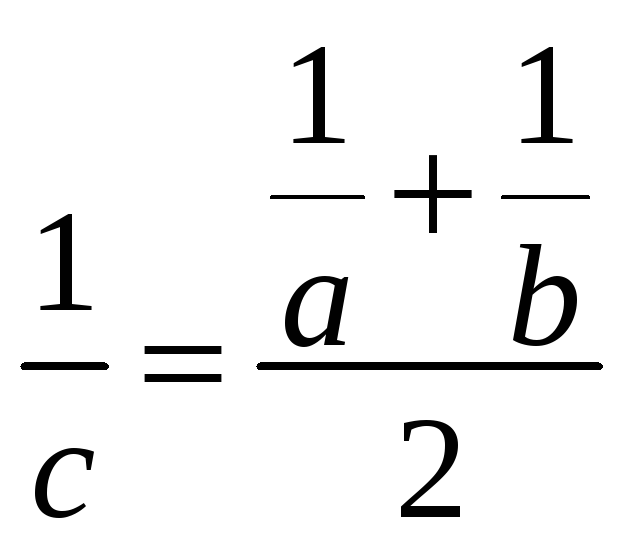
В выписанном ряде каждый член, начиная со второго, есть среднее гармоническое следующего и предыдущего членов ряда.

Исследуем данный ряд на сходимость с помощью критерия Больцано-Коши.

, поэтому данный ряд расходится.

§2.4. Абсолютная и условная сходимости рядов.

Определение Ряд (А) называется абсолютно сходящимся, если вместе с ним сходится ряд из абсолютных величин его членов: .

Теорема Коши (достаточный признак абсолютной сходимости ряда).

Если ряд сходится, то сходится и сам ряд (А).

Доказательство:

Пусть ряд сходится. Рассмотрим отрезок исходного ряда (А):

Определение Ряд (А) называется условно-сходящимся, если он сам сходится, а ряд из абсолютных величин расходится.