4. Контрольные расчеты параметров аппроксимирующей функции

Для проверки расчетов, выполняемых на компьютере, необходимо выполнить вручную расчеты параметров аппроксимирующей функции для заданного набора базисных функций с целью получения тестовых данных. Ручные расчеты выполняются как минимум дважды (причем желательно

- 33 -

разными способами) до совпадения тестовых результатов. С тестовыми (контрольными) данными сопоставляются результаты расчетов на компьютере. Существенное расхождение тестовых и компьютерных расчетов требует ана-

лиза и корректировки вводимых данных, алгоритмов, программ, а возможно и тестовых расчетов. Ниже приведен контрольный расчет для двух исходных базисных функций φ₁(x) = 1, φ₂ (x) = x.

Пример.

1. Постановка задачи.

Исходная функциональная зависимость представлена в таблице парами значений x_i и y_i .

Найти параметры (С₁ и С₂) аппроксимирующей функции y = C₁ + C₂ x, пользуясь МНК. Поиск параметров осуществить, используя условия локального минимума критерия аппроксимации (т.е. решая систему нормальных уравнений). Оценить погрешность аппроксимации посредством критерия качества J и максимального по модулю отклонения аппроксимирующей функции от исходной.

2. Табличное представление исходных данных.

Таблица 2

i	1	2	3	4	5
x	0,0	1,0	2,0	3,0	4,0
y	0,0	1,0	8,0	27,0	64,0

3. Критерий аппроксимации (см. подразд. 2.1).

Согласно условию (2.5):

J(C₁, C₂ ) = min .

4. Условия минимума критерия аппроксимации и формирование нормальных уравнений.

В соответствии с требованием использования условий локального минимума (2.9) условия минимума J

=0 , =0 ,

= = 2() ,

- 34 -

= 2() ,

т.е. нормальные уравнения имеют вид

2()=0,

2()=0

или

C₁ ·5 + C₂,

C₁.

Введем обозначения

a₁₁=5 ; a₁₂= ; b₁= ,

a₂₁= ; a₂₂= ; b₂= .

Тогда систему нормальных уравнений можно записать посредством матричных обозначений

A C = B ,

где A=  матрица коэффициентов нормальных уравнений;

C=  вектор-столбец неизвестных (искомых параметров);

B=  вектор-столбец свободных членов системы.

3. Вычисление коэффициентов нормальных уравнений.

а₁₁ =5 ; а₁₂ = 0,0+1,0+2,0+3,0+4,0 = 10,0 ;

а₂₁ = а₁₂ = 10,0 ;

а₂₂ = 0,0² + 1,0² + 2,0² + 3,0² + 4,0² = 30,0;

в₁ = 0,0 + 1,0 + 8,0 + 27,0 + 64,0 = 100,0;

в₂ = 0,0 · 0,0 + 1,0 · 1,0 + 8,0 · 2,0 + 27,0 · 3,0 + 64,0 · 4,0 = 354,0.

- 35 -

Система нормальных уравнений имеет вид

6. Решение системы нормальных уравнений.

А. Метод Гаусса:

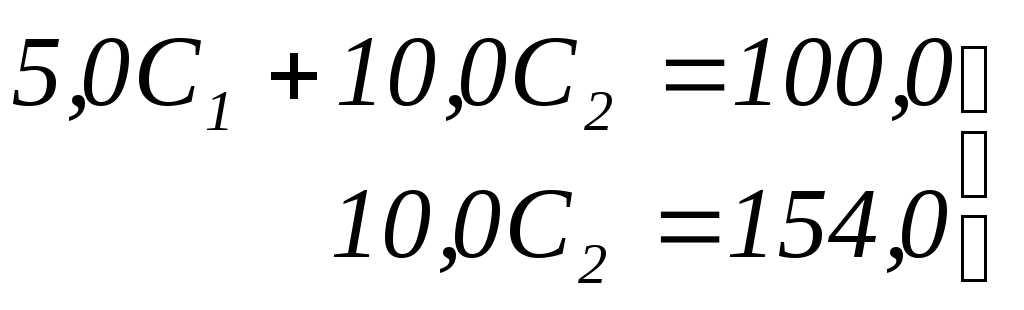С=15,4 ; С= -10,8

Б. Метод обратной матрицы:

для матрицы A =

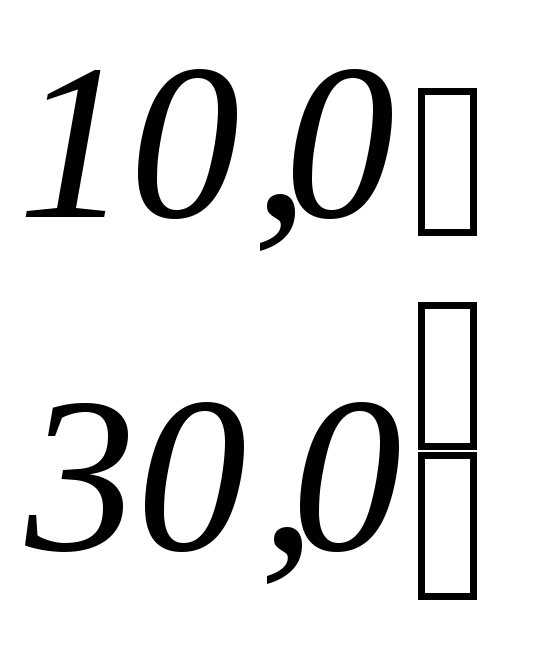
обратная матрица имеет вид

A^{-1 = ,}

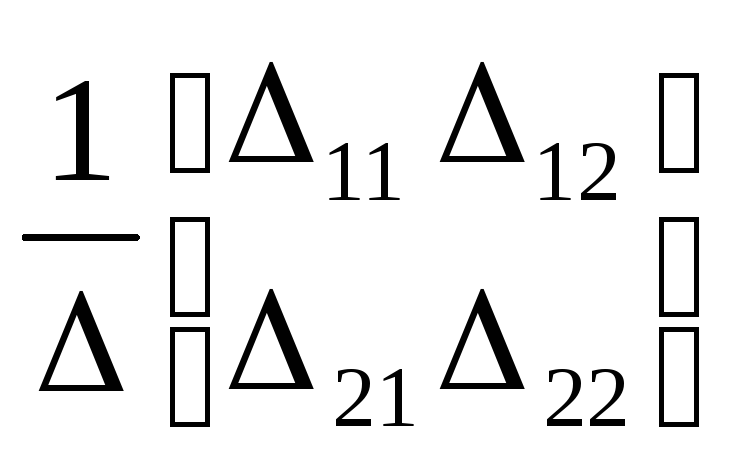где det A  определитель матрицы А;

_{i j}  алгебраическое дополнение.

Отсюда det A = 5 · 30,0 – 10,0 · 10,0 = 50,0.

A^-1 =

Решение системы уравнений A C = B методом обратной матрицы имеет вид C^* = A^-1 B, т.е.

C^* = ,

6. Запись искомой аппроксимирующей функции y(x)

y = –10,8 + 15,4 x .

8. Оценка погрешности аппроксимации.

Для оценки среднеквадратичного и максимального по модулю отклонений аппроксимирующей функции от исходной представим результаты проведенных вычислений в виде табл. 3 и рис. 13.

- 36 -

Таблица 3

i	xi	yi	y(xi)	i = yi – y(xi)
1 2 3 4 5	0,0 1,0 2,0 3,0 4,0	0,0 1,0 8,0 27,0 64,0	–10,8 4,6 20,0 35,4 50,8	10,8 –3,6 –12,0 –8,4 13,2

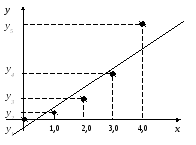
Рис. 13. График функций y=f(x), y=

Тогда минимальное значение качества аппроксимации

J_min = J(C) = (10,8)² + (–3,6)² + (–12,0)² + (–8,4)² + (13,2)² = 518,4,

а максимальное по модулю отклонение, получаемое сопоставлением найденных значений , составляет

max | | = 13,2 при x = x₅ = 4,0 .