Питання для самоперевірки

1. Які критерії називаються непараметричними?

2. Яка гіпотеза перевіряється за допомогою критерію Уїлкоксона?

3. Що таке інверсія і як вона визначається?

4. Як двома способами за допомогою критерію Уїлкоксона пере­вірити правильність гіпотези?

5. Як визначається критичне значення й критична область для критерію Уїлкоксона?

6. Що таке медіана? Як вона визначається для вибіркових значень?

7. Що таке серія знаків та як вона визначається ?

8. Як визначаються критичне значення та критична область для критерію знаків?

2.6 Перевірка гіпотез відносно частки ознаки порівняння двох вибірок

Критерії цієї групи дають змогу використовувати частку ознак і приймати рішення про власти­вість генеральної сукупності та відповідність нормам.

Будемо розглядати задачі: по­рівняння частки ознаки з норма­тивним значенням (стандартом) та порівняння частки ознаки у двох сукупностях.

Порівняння частки ознаки з нормативним значенням. Нехай потрібно перевірити гіпотезу, що частка р деякої ознаки у генераль­ній сукупності дорівнює деякому нормативному значенню α, тобто висувається нуль-гіпотеза Н₀: р = α при альтернативній гіпотезі Н₁: р≠α. Для перевірки гіпотези Н₀ застосовують двобічний критерій, оскільки порушення гіпотези Н₀ може бути як у разі р > α, так і в ра­зі р < α. Як критерій застосовуємо статистику

де n — загальна кількість випробувань; m — кількість позитивних результатів, W — частота.

Ця статистика при будь-якому n розподілена за біноміальним (для вибірки з поверненням) або за гіпергеометричним (для вибірки без по­вернення) законом розподілу. Однак при достатньо великому n при розрахунках можна скористатися асимптотичними розподілами, най­частіше — нормальним.

Виходячи з нормального закону розподілу при заданому рівні значущості α значення z знаходять із таблиць нормального розподі­лу згідно з рівністю:

Узявши до уваги, що для біноміального закону а також, що q=1-р і для розглянутого випадку вихідним припущен­ням p=α, дістанемо вираз

який надалі можна використати для знаходження надійних меж для W. Критичні точки в цьому випадку

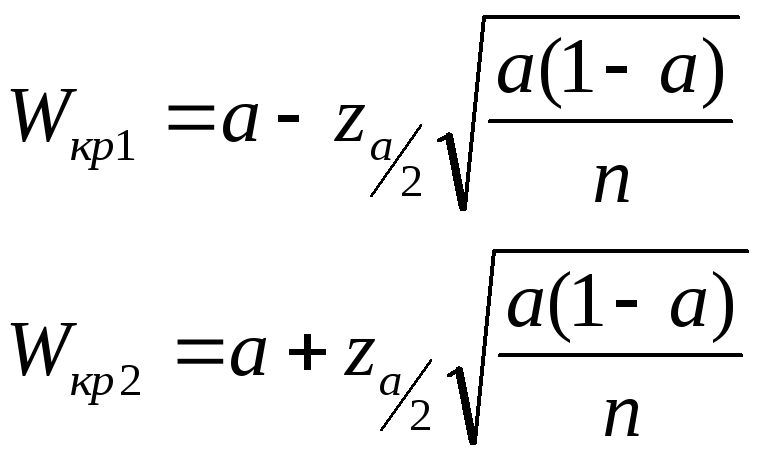
Якщо вибіркова частість W буде в межах [W₁, W₂], гіпотеза H₀ приймається.

У випадку, коли перевіряють альтернативну гіпотезу Н₁: р>α, використовують однобічну критичну область із граничним значен­ням z згідно з рівнянням

Приклад. Перевіряється внесок деякого компонента до складу продукції.

1. Перевірити відповідність вкладу складової 10%-ному стандар­тному значенню, тобто перевірити гіпотезу H₀: р = 0,1.

2. Перевірити, що наявність цього компонента у продукції не пе­ревищує 10%, тобто перевірити гіпотезу Н₁: р>α.

Порівняння частки ознаки у двох сукупностях. Припустимо, що маємо m₁/n₁ та m₂/n₂ частки однієї ознаки у двох сукупностях з n₁ та n₂ одиниць. Висувається гіпотеза H₀: розбіжність між m₁/n₁ та m₂/n₂ є ре­зультатом впливу випадкових факторів та обмеженого обсягу вибірок.

Розглянемо випадок великих вибірок. Якщо n₁ та n₂ більші за 30, то розподіл вибіркових частостей при виконанні припущення про нульову розбіжність буде близьким до нормального з параметрами

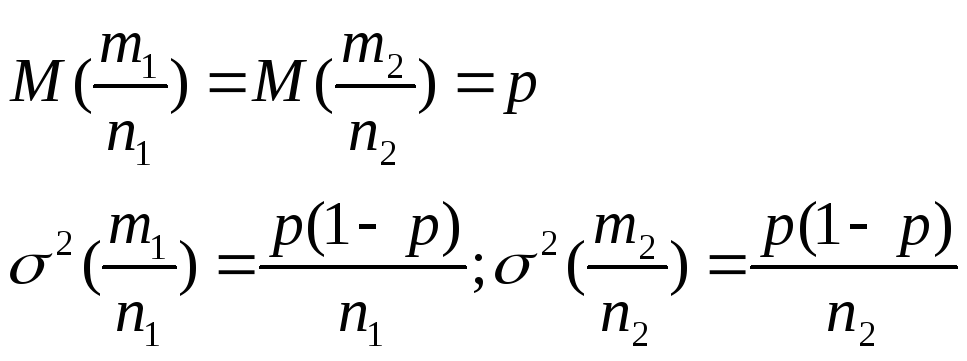
Для перевірки гіпотези застосовують статистику

Статистика W також може бути подана за допомогою нормально­го закону з параметрами

Для перевірки гіпотези H₀ будемо використовувати двобічний критерій. Задаючись рівнем значущості α, знаходимо z згідно з рів­нянням

а потім визначимо критичні точки

де — оцінка p, яку отримують на підставі на­явних даних двох вибірок.

Якщо вибіркове значення W вміститься в інтервалі [W_кр1, W_кр2], то гіпотеза про несуттєвість розбіжності приймається.

Розглянемо випадок малих вибірок. Якщо n₁ та n₂ - малі числа, то використання нормального розподілу для статистики є хибним. У цьому випадку необхідно використовувати критерій χ² за допомогою якого, як було показано раніше, при ідентифікації зако­нів розподілу можна визначити розбіжність між теоретичними і ви­бірковими частками.

Для розглянутого випадку χ² обчислюється в такий спосіб. При­пустимо, що нас цікавить деяка ознака А. Беруть дві сукупності об­сягами n₁ та n₂ і результати для позитивних А і негативних нас­лідків заносять у табл. 2.1.

У таблиці ₁, і ₂ — кількість елементів у кожній вибірці, які це мають ознаки А. Виходячи з припущення, що вибірки взято з ті­єї самої генеральної сукупності з часткою ознаки р, можна визначити теоретичні частоти, які відповідають фактичним частотам pn₁, (1-p)n₁, pn₂, (1-p)n₂.

Таблиця 2.1

Сукупність	Фактичні частоти			Оцінки теоретичних частот
	А		Усього	А
Вибірка 1	m1		n1	pn1	(1-p)n1
Вибірка 2	m2		n2	pn2	(1-p)n2
Усього	m1+ m2	+	n1+ n2	--	--

В останніх двох рядках табл. 19.1 наведені оцінки теоретичних частот, де замість р використовується = (m₁, +m₂)/(n_І + n₂).

На підставі даних, наведених у табл. 19.1, можна обчислити χ² за формулою:

де у знаменниках записано оцінки відповідних дисперсій.

Беручи до уваги, що між чотирма теоретичними частотами існує три незалежні співвідношення, у розподілі χ² необхідно враховувати тільки один ступінь свободи.

Якщо нульова гіпотеза, відповідно до якої обидві сукупності є вибірками з однієї генеральної сукупності, правильна, то розбіжність між теоретичними та дослідними частотами можна віднести тільки на рахунок випадкового відбору. Тому, визначивши для рівня значущості α значення χ², приймемо рішення про відхилення гіпотези H₀, якщо, незначущість розбіжності при .

Приклад. Проводились випробування нового методу лікування. Одна група (експериментальна) — з 50 осіб (n₁ = 50) лікувалася за новим методом, а друга («традиційна»), яка складалася з 30 осіб (n₂ = 30), — за традиційним методом. Після завершення лікування у першій групі залишилося 9 хворих (m₁=9), а в другій — 7 (m₂=7). Необхідно перевірити суттєвість ефективності нового методу.

Обчислимо оцінку теоретичної частоти хворих після лікування:

Позначимо позитивний результат для хворого — «вилікувалися за зазначений період» як подію А, тоді — «залишилися хворими» буде . Вихідні дані та отримані результати наведено в табл. 2.2.

Таблиця 2.2

Групи, що обстежуються	Результати досліджень		Усього	Теоретичні результати
	А			А
Експериментальна	9	41	50	10	40
«Традиційна»	7	23	30	6	24
Усього:	16	64	80

Розрахунок теоретичної кількості позитивних результатів будемо проводити відповідно за виразами та . Внесемо у табл. 19.2 оцінку теоретичної кількості А та . Виходячи з даних, наведених у табл. 19.2, обчислимо значення критерію:

Скориставшись таблицями розподілу χ², для α= 0,05 та ступеня свободи f=1, знайдемо критичне значення χ²_кр =3,8. Таким чином, , тобто робимо висновок, що розбіжність частки хворих, які залишилися в обох групах після закінчення терміну лікування, не значуща, а отже, новий метод лікування дає такий самий ефект, як і традиційний.

Порівняння двох залежних вибірок (парні зіставлення). У практиці статистичної перевірки гіпотез часто трапляються випадки, коли дві вибірки, які порівнюються, не можуть розглядатися як незалежні.

Приклад. Перевірка ефективності нової технології за результатами роботи тієї самої бригади до і після впровадження нової технології.

Приклад. Оцінка стану хворих до і після прийняття нових ліків. Проводячи реєстрацію по кожному об'єкту спостережень до нововведення — х і після нього —у, дістаємо два ряди спостережень:

x1	x2	…	xi	…	xn
y1	y2	…	yi	…	yn

Таким чином, ідеться про парні спостереження, тобто про n зв'язаних пар (х_i, у_i). Якщо досліджуваний фактор впливає тільки на одну з ознак х або у, то між цими парами спостережень фіксувати­меться суттєва розбіжність. Завдання полягає в тому, щоб визначи­ти, коли розбіжність між парами спостережень можна віднести на рахунок випадкових відхилень, а коли вона суттєва і її потрібно пов'язувати з впливом якогось фактору.

Нехай різниця між спостереженнями в кожній парі становить Тоді узагальненою величиною розбіжності пар спостережень може бути середня різниця

(2.21)

Чим менша різниця , тим більш правдоподібне припущення що­до несуттєвості розбіжності між рядами спостережень. Таким чином, перевірці підлягає гіпотеза H₀:. Критерієм для перевірки може бути статистика

(2.22)

де

При нормальному розподілі різниць t-статистика має роз­поділ Стьюдента з кількістю ступенів свободи n - 1. Подальший ме­ханізм перевірки не відрізняється від перевірки розбіжності середніх.

Перевірку гіпотез широко використовують у дисперсійному аналізі та в теорії кореляції, де перевіряють гіпотези про значущість відповідних параметрів, наявність стохастичного зв'язку, суттєвість впливу випадкових величин тощо.