20) Пересечение плоскостей

Линия пересечения двух плоскостей — прямая линия. Рассмотрим сначала частный случай

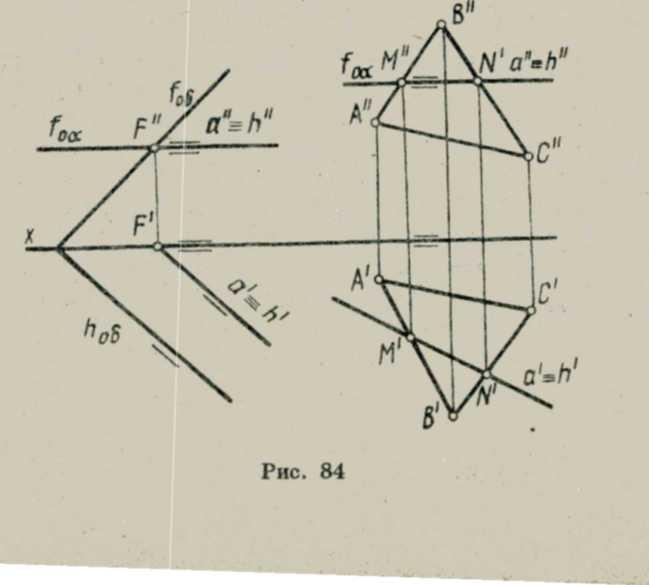
, когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций. В этом случае линия пересечения а, принадлежащая плоскости а, будет также параллельна плоскости тс,, т. е.. будет являться горизонталью пересекающихся плоскостей. Если одна из плоскостей параллельна фронтальной плоскости проекций рис. 85 то линия пересечения Ь, принадлежащая плос­кости р, будет параллельна плоскости п₂ (b = f — фрон­таль пересекающихся плоскостей).

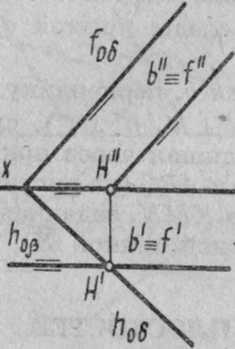
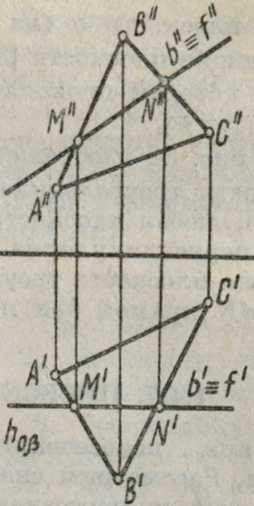
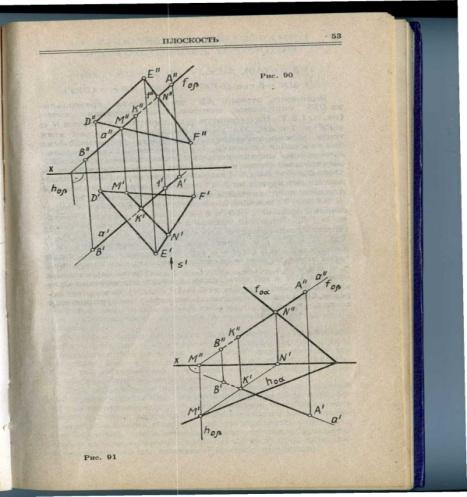
В общем случае (рис. 86) линия пересече­ния плоскостей определя­ется при помощи вспомо­гательных секущих плос­костей 8. На рис. 86 по­казаны две произвольно расположенные в про­странстве плоскости а и В, соответственно заданные плоскими фигурами (тре­угольниками ABC и DEF).

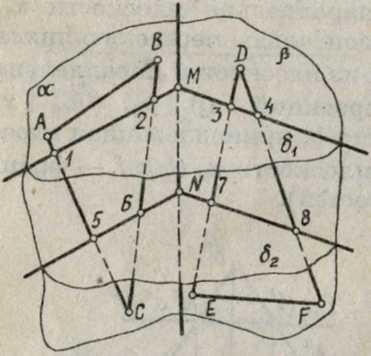
Для определения точ­ки, принадлежащей ли­нии пересечения плоскос­тей а и В, проведена произвольная вспомогательная секущая плоскость 8_1г которая пересекает заданные плоскости а и р соответственно по линиям 12 и 34.

Точка пересечения этих линий (М = 12 г 34) при­надлежит всем трем плоскостям а, Р и 8, а следова­тельно, и линии пересечения заданных плоскостей а и р.

Проведя вторую вспомогательную секущую плос­кость 8₂ и выполнив аналогичные построения,

вторую точку, принадле­жащую линии пересече­ния плоскостей (N = 56 п п 78).

Вспомогательные секу­щие плоскости обычно вы­бираются параллельными плоскостям проекций (рис. 87 и 88).

Ha рис. 88 показан пример построения линии пере­сечения плоскостей аир, заданных следами.

21) Пересечение прямой с плоскостью

На рис. 89 показано построение точки К пересечения прямой а (АВ) с плоскостью a (DEF). Прямая а за­ключена в произвольную плоскость Р, и определена линия пересечения плоскостей аир (MN = а n Р).

Прямые АВ и MN принадлежат одной плоскости р и пересекаются в точке К, а так как прямая MN при­надлежит заданной плоскости a (DEF), то точка К яв­ляется и точкой пересечения прямой а (АВ) с плоскос­тью а (К = а п а). Алгоритм построения точки пересе­чения прямой а с плоскостью а может быть записан в виде (рис. 90)

22) Многогранники основные понятия и определения. Изображение многогранников

Многогранником называется геометрическое тело, ог­раниченное со всех сторон плоскими многоугольниками.

Плоские многоугольники, ограничивающие много­гранник, являются его гранями, а линии пересечения граней (стороны многоугольников) ■— его ребрами.

Концы ребер называются вершинами многогранника. По числу граней многогранники бывают четырехгран­ные, пятигранные и т. д. Различают многогранники вы­пуклые и вогнутые. Многогранник называется выпук­лым, если он весь расположен по одну сторону от любой его грани.

Правильным многогранником называется такой вы­пуклый многогранник, у которого все грани — одина­ковые правильные многоугольники и все многогранные углы при вершинах равны.

Наиболее распространенными в инженерной практи­ке многогранниками являются пирамиды и призмы.

многоугольник, а осталь­ные грани — треугольни­ки, имеющие общую вер­шину S.

По числу углов много­угольника основания раз­личают пирамиды тре­угольные,

Если вершина пирамиды S проецируется ортогональ­но в центр тяжести ее основания, то такая пирамида называется прямой. Правильной пирамидой называется такая прямая пирамида, основанием которой является правильный многоугольник.

ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ НА ОРТОГОНАЛЬНОМ ЧЕРТЕЖЕ

На ортогональном чертеже любой многогранник может быть задан: проекциями его вершин (точками), ребер (отрезками прямых) и граней (плоскими фигура­ми).

Вершины многогранника заданы точками А, В, С и S, ребра — отрезками прямых АВ, ВС, СА, AS, BS и CS, а грани — треугольни­ками ABC, ABS, BCS и CAS.

Видимость ребер много­гранника на ортогональ­ном чертеже определяется с помощью следующих правил.

1. Проекции ребер, ко­торые образуют внешний контур проекции много­гранника, всегда видны. Это проекции ребер А"В", В"С", C"S" и S"A" на фрон­тальной плоскости проек­ций и А'В', B'S', S'C и СА' — на горизонтальной плоскости проекций.

2. Видимость осталь­ных ребер многогранника

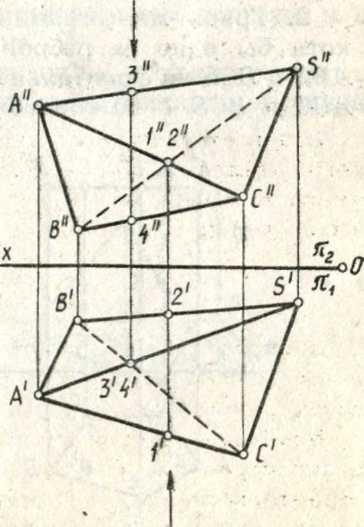
Рис. 27

определяется методом конкурирующих точек

Видимость граней многогранника на ортогональном чертеже определяется с помощью следующих правил.