60. Докажите что подобные матрицы имеют одинаковые характеристические многочлены.

Рассмотрим подобные матрицы A и B = C−1AC, где C - невырожденная матрица. Тогда

fB = |B −λE| = |C−1AC −λE| = |C−1AC −C−1(λE)C| = |C−1(A−λE)C| = |A−λE| = fA

Что и требовалось показать.

61. Дайте определение числа Фробениуса неотрицательной квадратной матрицы. Найдите число Фробениуса для матрицы : (а) ; (б) . Ответы обоснуйте.

Числом Фробениуса матрицы A ≥ 0 называется максимальное собственное значение

этой матрицы.

Теорема: Если сумма элементов строки (столбца) матрицы A > 0 одинакова и

равна a, то число Фробениуса матрицы A равно a.

1. матрица 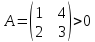Сумма элементов всех строк равна 5. Следовательно, опираясь на теорему, число Фробениуса этой матрицы равно 5.

b) Найдем собственные значения матрицы

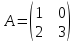
(1-λ)(3-λ) = 0

λ = 1, λ = 3

Числом Фробениуса называется максимальное собственное значение, то есть = 3

62. Дайте определение продуктивной матрицы. Докажите продуктивность матрицы А=(0.2 0.6 0.9 0.3)

Теорема: Матрица A ≥ 0 продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.

Найдем собственные значения матрицы A :

(0.2 − λ)(0.3 − λ) − 0.54 = 0

−0.48 − 0.5λ + λ2 = 0

D = 0.25 + 4 · 0.48 = 0.25 + 1.92 = 2.17

λmax = 0.5+√2.17 /2

√2.17 < 1.5 = √2.25 ⇒ λmax < 0.5+1.5/2 = 1

Число Фробениуса меньше 1, а значит матрица A по определению является продуктивной.

63. Сформулируйте критерий продуктивности матрицы. Приведите пример продуктивной матрицы порядка 3*3

Теорема: Матрица A ≥ 0 продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.

Теорема: Если сумма элементов ∀ строки ( ∀ столбца) матрицы A > 0 одинакова и равна a, то число Фробениуса матрицы A равно a.

Пример: Рассмотрим матрицу A =

0.2 0.7

0.5 0.4

По теореме (сумма элементов всех строк равна 0.9) число Фробениуса равно λA = 0.9 < 1, а значит (по критерию) рассматриваемая матрица продуктивна.

7. Квадратичные формы

64. Дайте определение матрицы квадратичной формы. Найдите матрицу квадратичной формы:

а) ;

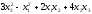б) .

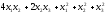Квадратичной формой Ф от переменных x₁,x₂,…x_n называется однородный многочлен второй степени от этих переменных. Каждая квадратичная форма допускает однозначную запись в следующем симметричном виде:

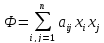
Где a_ij­=a_ji (матрица симметрическая)

Симметрическая матрица А, элементами которой являются числа a_ij, называется матрицей квадратичной формы Ф. Если ввести в рассмотрение столбец X=(x₁;x₂;…;x_n)^T, то квадратичную форму Ф можно записать в матричном виде Ф=X^TAX.

_А)

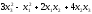
_Б)

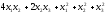
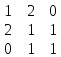
65. Сколько линейно независимых собственных векторов может иметь матрица порядка 3*3

Так как матрица 3 × 3, то характеристический многочлен имеет 3ий порядок, а это значит, что корней (собственных значений матрицы) не более 3, тем более различных действительных корней у многочлена 3ьей степени не более 3.

Теорема (о линейной независимости собственных векторов): Собственные векторы квадратной матрицы, отвечающие различным собственным значениям, линейно независимы.

Следовательно, опираясь на теорему можно утверждать, что действительная симметрическая матрица порядка 3 × 3 имеет не более 3 линейно независимых собственных векторов.