
- •Натуральные числа
- •Метод математической индукции.
- •Бином Ньютона, треугольник Паскаля
- •Целые числа
- •Рациональные числа
- •Числовые кольца, поля
- •Вещественные числа
- •Поле комплексных чисел
- •Комплексная плоскость.
- •Извлечение корней, корни из единицы
- •Делимость многочленов. Наибольший общий делитель. Алгоритм Евклида. Расширенный алгоритм Евклида.
- •Разложение рациональных функций в сумму дробей.
- •Неприводимый многочлен, его свойства
- •Из вытекает, либо , либо .
- •Если неприводимый многочлен делится на неприводимый многочлен, то они отличаются числовым множителем.
- •Корень многочлена.
- •Интерполяционный многочлен
- •Интерполяционный многочлен в форме Лагранжа
- •Интерполяционный многочлен в форме Ньютона
- •Разложение многочлена над полем рациональных чисел
- •Примитивный многочлен, его свойства
- •Критерий Эйзенштейна
- •Все коэффициенты многочлена f(X), кроме старшего, делятся на p
- •Старший коэффициент не делится на p
- •Свободный член не делится на
- •Метод Кронекера разложения многочлена на неприводимые многочлены над кольцом целых чисел.
- •Рациональные корни.
- •Присоединение корня. Поле разложения многочлена.
- •Формальная производная, ее свойства
- •Производные высоких порядков
- •Интерполяционный многочлен Лагранжа-Сильвестра
- •Формулы Виета
- •Симметрические полиномы
- •Формулы Кардано
- •Способ Феррари
- •Дискриминант
- •Основная теорема Алгебры
- •Разложение многочлена на неприводимые множители над полем вещественных чисел
- •Теорема Штурма
- •Любые два соседних многочлена не имеют общих корней
- •Последний многочлен не имеет вещественных корней.
- •Если в окрестностях корня a многочлена сам многочлен возрастает, то , а если убывает, то
- •Метод Гаусса решения системы линейных уравнений
- •Равносильные преобразования
- •Умножение строки не ненулевое число.
- •Перестановка строк
- •Прибавление к некоторой строке другой строки, умноженной на число.
- •Метод Гаусса.
- •Перестановки
- •Четность перестановок
- •Определитель
- •Свойства определителя
- •Изменит знак при перестановке столбцов
- •Равен нулю, если имеется два одинаковых столбца
- •Не изменится при прибавлении к столбцу другого столбца, умноженного на число.
- •Вычисление определителей произвольных порядков
- •Определитель Вандермонда
- •Теорема Лапласа
- •Умножение матриц
- •Формула Бине-Кощи
- •Операции с матрицами
- •Обратная матрица
- •Правило Крамера
- •Матрица элементарных преобразований
- •Построение обратной матрицы
- •Блочные матрицы
- •Алгоритм Штрассена
- •Кронекерово произведение
- •Формула Фробениуса
- •Линейные пространства.
- •. Линейная зависимость. Теорема о замене. Ранг системы.
- •Конечномерные пространства. Базис. Размерность. Дополнение до базиса. Базис суммы, пересечения.
- •. Прямая сумма подпространств. Проекция.
- •Изменение координат вектора при изменении базиса.
- •Изоморфизм линейных пространств.
- •Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.
- •Ранги матрицы.
- •Общее решение системы линейных уравнений.
- •Двойственное пространство
- •Взаимное расположение линейных многообразий в пространстве.
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Симметричность .
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
-
Разложение многочлена на неприводимые множители над полем вещественных чисел
Рассмотрим многочлен с вещественными
коэффициентами
![]() .
Над полем комплексных чисел он
раскладывается на линейные множители.
Если a его комплексный
корень, то
.
Над полем комплексных чисел он
раскладывается на линейные множители.
Если a его комплексный
корень, то
![]() ,
т.е.
,
т.е.
![]() то же корень f(x).
Таким образом, многочлен f(x)
делится на трёхчлен
то же корень f(x).
Таким образом, многочлен f(x)
делится на трёхчлен
![]() с вещественными коэффициентами. Тем
самым устанолена
с вещественными коэффициентами. Тем
самым устанолена
Теорема 2.25. Над полем вещественных чисел многочлен раскладывается в произведение неприводимых многочленов степени 1 и 2. Разложение единственно с точностью до перестановки сомножителей.
-
Теорема Штурма
Определение 2.8Последовательность
многочленов
![]() назовём последовательностью многочленов
Штурма, если она удовлетворяет следующим
условиям:
назовём последовательностью многочленов
Штурма, если она удовлетворяет следующим
условиям:
-
Любые два соседних многочлена не имеют общих корней
-
Если a – корень
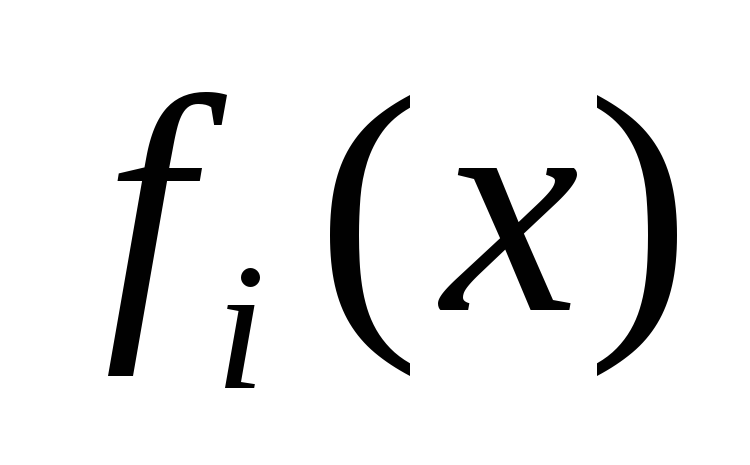 при i>0, то
при i>0, то
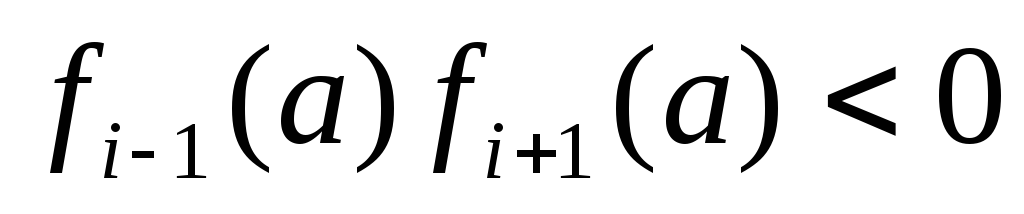
-
Последний многочлен не имеет вещественных корней.
-
Если в окрестностях корня a многочлена сам многочлен возрастает, то , а если убывает, то
Для последовательности многочленов F
и числа a определим w(a)
– число перемен знака в числовой
последовательности
![]() (нули игнорируем).
(нули игнорируем).
Теорема 2.26 Штурма
Число различных корней многочлена
![]() на отрезке
на отрезке
![]() равно
равно
![]() .
.
Доказательство.
Пусть
![]() корни многочленов из ряда Штурма F,
принадлежащие отрезку
корни многочленов из ряда Штурма F,
принадлежащие отрезку
![]() и упорядоченные в порядке возрастания.
Поскольку, многочлен может изменить
знак только при прохождении через
корень, то для любых точек из интервала
и упорядоченные в порядке возрастания.
Поскольку, многочлен может изменить
знак только при прохождении через
корень, то для любых точек из интервала
![]() число перемен знака заведомо одно и
тоже. Если
число перемен знака заведомо одно и
тоже. Если
![]() корень многочлена
корень многочлена
![]() (i>0)
то последовательность
(i>0)
то последовательность
![]() при достаточно малом по модулю значению
y
даёт только одну перемену знака, т.к.
по условию II
на концах стоят числа разных знаков.
Следовательно, число перемен знака
может измениться только при прохождении
через корень многочлена
при достаточно малом по модулю значению
y
даёт только одну перемену знака, т.к.
по условию II
на концах стоят числа разных знаков.
Следовательно, число перемен знака
может измениться только при прохождении
через корень многочлена
![]() .
По условию IV,
число перемен знака может только
уменьшаться.
.
По условию IV,
число перемен знака может только
уменьшаться.
Пусть многочлен f(x)
не имеет кратных корней. Построим
последовательность многочленов:
![]() ,
,
![]() ,
и далее,
,
и далее,
![]() - остаток от деления
- остаток от деления
![]() на
на
![]() умноженный на -1.
умноженный на -1.
Данная последовательность многочленов
будет последовательностью многочленов
Штурма. Действительно, условие IV
выполнено по свойству производной.
Наибольший общий делитель многочлена
и его производной равен 1, т.к. нет кратных
корней. Таким образом, последний многочлен
в ряду равен константе и не имеет
вещественных корней. Из равенства
![]() вытекает
условие II. Подставив x=a,
где a – корень
вытекает
условие II. Подставив x=a,
где a – корень
![]() ,
получим
,
получим
![]() .
Общего корня у соседних многочленов не
может быть, так как его наличие приводит
к существованию кратных корней у
.
Общего корня у соседних многочленов не
может быть, так как его наличие приводит
к существованию кратных корней у
![]() .
.
-
Метод Гаусса решения системы линейных уравнений
Ряд задач алгебры приводит к задаче
построения решения системы линейных
уравнений. Например, вычисление
коэффициентов интерполяционного
многочлена методом неопределённых
коэффициентов. В общем виде задача
отыскания решения системы линейных
уравнений выглядит следующим образом.
Найти набор чисел
![]() при подстановке которых вместо переменных
при подстановке которых вместо переменных
![]() все уравнения системы
все уравнения системы
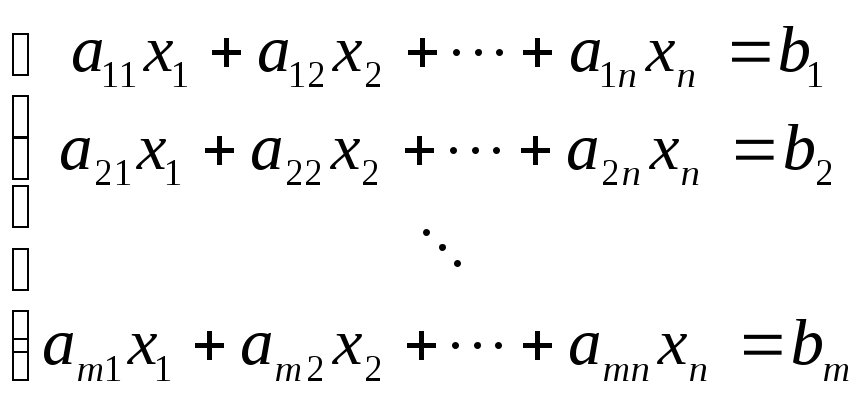 обращаются в равенства.
обращаются в равенства.
Запишем таблицу чисел, образованную
коэффициентами при неизвестных
 .
В алгебре принято называть прямоугольную
таблицу чисел матрицей. Припишем к
матрице коэффициентов правые части
уравнений
.
В алгебре принято называть прямоугольную
таблицу чисел матрицей. Припишем к
матрице коэффициентов правые части
уравнений
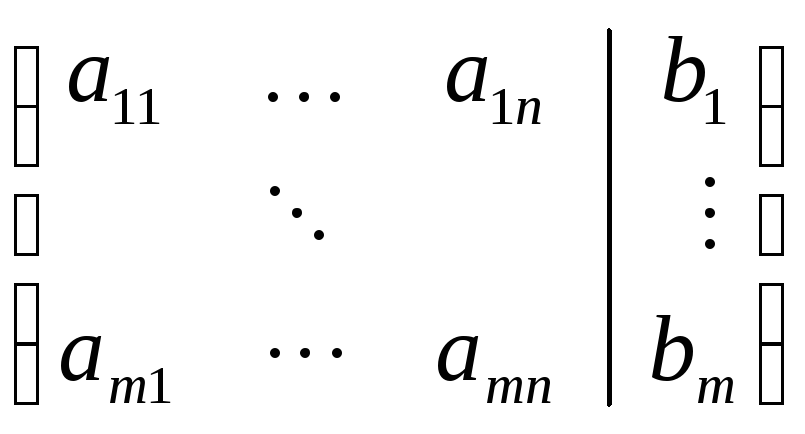 отделив их от матрицы коэффициентов
вертикальной чертой. Получившаяся
матрица называется расширенной матрицей
системы линейных уравнений. В дальнейшем
нам будет удобнее работать не с системой
линейных уравнений, а с её расширенной
матрицей.
отделив их от матрицы коэффициентов
вертикальной чертой. Получившаяся
матрица называется расширенной матрицей
системы линейных уравнений. В дальнейшем
нам будет удобнее работать не с системой
линейных уравнений, а с её расширенной
матрицей.
