
- •1. Анализ вариации зависимой переменной в регрессии
- •2. Тест Дарбина – Уотсона некоррелированности случайных возмущений в схеме Гаусса – Маркова
- •3. Метод имитационного моделирования. Исследование последствий нарушения условий теоремы Гаусса – Маркова
- •4. Анализ вариации зависимой переменной в регрессии
- •5. Коэффициент детерминации как мера качества спецификации эконометрической модели
- •6. Компьютерное моделирование эконометрических систем
- •8. Процедура точечного прогнозирования по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной
- •9. Интервальное прогнозирование по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной
- •10. Множественная линейная регрессионная модель. Оценивание параметров множественной регрессии методом наименьших квадратов
- •11. Определение границ доверительных интервалов точечных оценок множественной регрессионной модели
- •12. Оценивание параметров модели взвешенным методом наименьших квадратов
- •13. Модель Марковица
- •14. Определение границ доверительного интервала прогноза зависимой переменной
- •15. Проверка гипотез относительно коэффициентов парной регрессии
- •16. Автокорреляция случайного возмущения
- •17. Гетероскедастичность случайного возмущения
- •18. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели множественной регрессии
- •19. Модель парной регрессии. Границы доверительных интервалов
- •20. Гетероскедастичность случайной компоненты. Тесты на наличие гетероскедастичности
- •21. Автокорреляция случайной составляющей. Тесты на наличие автокорреляции
- •22. Спецификация и преобразование к приведенной форме динамических моделей. Лаговые и предопределенные переменные динамической модели
- •23. Уточнение эконометрических моделей путем датирования переменных
- •24. Парная регрессия. Оценивание параметров методом наименьших квадратов
- •25. Тест Голдфелда–Квандта гомоскедастичности случайных возмущений в схеме Гаусса – Маркова
- •26. Дисперсионный анализ в парной регрессии
18. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели множественной регрессии
Основная спецификация математической модели: Yt = a0 +a1X1t +...+akXkt +ἐt
X1t...
Xkt
- экзогенная
независимая переменная, Yt
- эндогенная зависимая переменная, a0...
ak
- неизвестные
коэффициенты регрессии, подлежащие
оценки, ἐt
-
последовательность случайных величин,
удовлетворяющие условиям теоремы
Гаусса-Маркова.
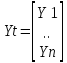 ,
,
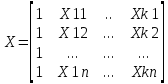 ;
;
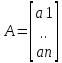 ;
;
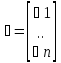 ;
;
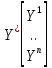
Y^=
XA= *
* ;
;
В
соответствии
с
МНК
найдем
minESS: min(поА)
(Y-XA)T(Y-XA)=min(YTY-2ATXTY+ATXTXA),
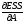 =
-2XTY+2XTXA=0.
Откуда
получим систему нормальных уравнений:
XTXA=
XTY,
то A
= (X*XT)-1XTY
=
-2XTY+2XTXA=0.
Откуда
получим систему нормальных уравнений:
XTXA=
XTY,
то A
= (X*XT)-1XTY
19. Модель парной регрессии. Границы доверительных интервалов
Наша
задача – подобрать функцию так, чтобы
она проходила на наименьшем расстоянии
от всех точек сразу. Для этого необходимо
минимизировать выражение
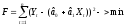 Необходимые
условия экстремума:
Необходимые
условия экстремума:
 Возьмем
соответствующие производные и приравняем
их к нулю:
Возьмем
соответствующие производные и приравняем
их к нулю:
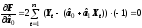 ;
; .
.
Раскроем
скобки и получим стандартную форму
нормальных уравнений:
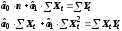
Решая
систему уравнений относительно получаем
их оценки: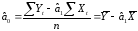
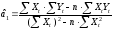
Из
последнего уравнения получаем:
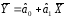 .
Это равенство указывает на то, что
уравнение регрессии проходит через
точку
.
Это равенство указывает на то, что
уравнение регрессии проходит через
точку
 .
Обозначим
.
Обозначим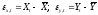 .
Подберем линейную функцию
.
Подберем линейную функцию
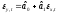 минимизирующую функционал
минимизирующую функционал
 .
Это будет та же прямая, только в новых
координатах, центр которых переместится
в точку
.
Это будет та же прямая, только в новых
координатах, центр которых переместится
в точку
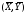 .
Так как
.
Так как
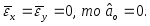 и
и
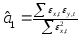 .
.
Регрессионное
уравнение имеет вид
 ,
где Xt – случайная величина, не
коррелированная с ε. εt – случайная
величина. Yt – объясняемая (зависимая)
переменная, Xt – объясняющая (независимая)
переменная.
Поскольку
Yt является суммой случайной переменной
Xt и случайной переменной ε t , то она
сама является случайной величиной.
Основные гипотезы относительно модели:
,
где Xt – случайная величина, не
коррелированная с ε. εt – случайная
величина. Yt – объясняемая (зависимая)
переменная, Xt – объясняющая (независимая)
переменная.
Поскольку
Yt является суммой случайной переменной
Xt и случайной переменной ε t , то она
сама является случайной величиной.
Основные гипотезы относительно модели:
1.
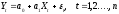 - спецификация
модели
- спецификация
модели
2. Xt – случайная величина, не коррелированная с ε.
3. М(ε)=0
4. М(ε2)=σ2 = const - не зависит от t
5. M(εt, εs ) = 0 при t ≠ s – некоррелированность значений случайной составляющей в различные моменты времени
Условия 3, 4, 5 называются условиями Гаусса-Маркова
Прогноз
будущего (или пропущенного) значения
эндогенной переменной определяется по
уравнению регрессии. Найдем доверительный
интервал, который с доверительной
вероятностью Р = 1 – α
будет накрывать значение зависимой
переменной Y^: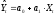 .
.
Доверительный интервал определяется разбросом случайной компоненты относительно уравнения регрессии. Причин этого разброса две:
-
Оценки коэффициентов регрессии
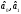 являются величинами случайными и они
сами по себе создают разброс относительно
истинного уравнения регрессии.
являются величинами случайными и они
сами по себе создают разброс относительно
истинного уравнения регрессии. -
Случайная составляющая εt
Ошибка
предсказания равна

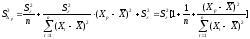
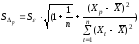 ;
;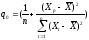 ;
;
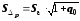
Тогда границы интервала будут задаваться так: (Y^ - tα*S∆p; Y^ + tα*S∆p), где tα - статистика Стьюдента.
20. Гетероскедастичность случайной компоненты. Тесты на наличие гетероскедастичности
Одно из требований теоремы Гаусса-Маркова - дисперсия случайной компоненты
D( )
=
)
=
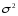 = const,
= const,
т.е. предположение о постоянстве дисперсии случайной составляющей для всех наблюдений. Если это условие соблюдается, процесс et называется гомоскедастичным. Если это не так, то процесс называется гетероскедастичным. Для обнаружения гетероскедастичности используется метод Голдфельда-Квадта. При проведении проверки по этому тесту предполагается сначала, что стандартное отклонение σ является случайной составляющей пропорционально значению одной из независимых переменных: X1t или Х2t .
Для того, чтобы осуществить проверку на гомоскедастичность, необходимо для начала сортировать имеющиеся данные по возрастанию одной из переменных X1t или Х2t. Важное условие такой сортировки – неразрывность троек (X1t,X2t,Yt), они могут перемещаться только вместе. В результате получаем новую таблицу, в верхней части которой сосредоточены меньшие значения Х1t, а в нижней – большие.
Далее делим получившийся массив данных на две (по возможности) равные части. Для каждой из частей определяем регрессию с помощью функции ЛИНЕЙН и выделяем значения ESS1 и ESS2.
Следующий
шаг – вычисление
статистик
 (статистика
Голдфельда-Квадта) и 1/GQ=ESS2/ESS1.
(статистика
Голдфельда-Квадта) и 1/GQ=ESS2/ESS1.
Статистика
GQ
является случайной
величиной, распределенной по закону
Фишера со
степенями свободы числителя
![]() и степенями свободы знаменателя
и степенями свободы знаменателя
![]() ,
где М – количество пар чисел в первой,
а L
– количество пар чисел во второй части
выборки.
,
где М – количество пар чисел в первой,
а L
– количество пар чисел во второй части
выборки.
Далее находим значение F-статистики Фишера, используя уровень значимости α (обычно равен 0,05), а также количество степеней свободы первой и второй части списка; проверяем условия

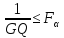
Если оба этих условия выполняются, то гипотеза о равенстве дисперсий в обеих половинах выборки принимается с вероятностью p=1-α. Если хотя бы одно из неравенств не выполняется, то гипотеза отвергается с той же вероятностью.
