Лекция №19.

Пусть задача квадратичного программирования имеет постановку:

F(x)=CX+X^TDX max

(1) AX<=B

X>=0

Предположим, что функция строго вогнутая, т.о. будем иметь задачу вогнутого нелинейного программирования.

Применяя теорему Куна-Таккера к задаче (1), можно получить необходимое условия задачи.

Составим функцию Лагранжа для задачи (1):

F(X, Л)=CX+X^TDX+Л(B-AX)

^dF =C+2DX-A^TЛ<=0

^dx

^dF =b-AX>=0

^dЛ

Введем два дополнительных вектора:

V>=0 и W>=0 (2)

С+2DX-A^T Л=0 (3)

B-AX-W=0 (4)

Теорема об оптимальности решения:

^x10

Вектор X₀= ^x20 <=0 является оптимальным решением

^…

^xn0

задачи ⁽0)тогда и только тогда, когда существуют такие неотрицательные вектора:

Л=(л1,л2,…лm)>=0

V=(v1,…vn)>=0

W=(w1,…wm)>=0, которые удовлетворяют условиям (3), (4) и условиям дополняющей нежесткости

X^TV=0 (5)

Л^TW=0 (6)

Т.о решение задачи квадратичного программирования (1) свелось к нахождению решения системы (n+m) линейных уравнений (3),(4),(5),(6) с (2(n+m)) неизвестными. Решение системы (3-6), если оно существует, то оно должно быть одним из допустимых базисный решений системы (3-4).

Для нахождения ДБР может быть использован обычный симплексный метод.

Алгоритм:

1. Для исходной задачи составляется функция Лагранжа.

2. Записывается условие Куна-Таккера.

3. Вводятся дополнительные вектора (V,W) и записывается система уравнений.

4. Записывается система уравнений в стандартной форме. Заполняется симплексная таблица , в которой отсутствует строка для целевой функции.

5. Применяя табличный алгоритм замены переменных, находят базисное решение. Найденное решение проверяется. Если удовлетворяет, то и оптимальным решением. Если неудовлетворяет ищется новое базисное решение и т.д.пока не будет найдено оптимальное решение либо установлено, что несуществует оптимального решения.

Замечание; Решение допустимого базисного решения должно удовлетворять решениям нежесткости. И при замене переменных необходимо менять переменные;

V ;

Л W ;

ГЕОМЕТРИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

ГП - это еще один класс задач нелинейного программирования. В ГП как оптимальная функция так и ограничения относятся к позиномиальным функциям.

Позиномом называется функция m переменных вида;

( … )=. .…… (1)

где

0 ,0 j=1,n

-вещественные числа

Задача ГП в общем случае формулируется следующим образом;

(…)=min (2)

(….)=….1 (2)

k=1,n-кол-во ограничений

0

найти min :

-множество

=

=

-входящие как в функцию так и в ограничения образуют матрицу экспонент.

A=

Кол-во столбцов =кол-ву переменных

Кол-во строк =кол-ву позиномов, входящих в функцию и в ограничения.

Каждой строке матрицы соответствует один позином.

Функция (1) называется прямой функцией, а ограничения (2)

Называются вынужденными ограничениями.

Лекция 20. Задача геометрического программирования с ограничениями.

Прямая функция :

(1)

где

Двойственная задача :

(2)

, , , , (3)

, где - двойственные переменные ;

число двойственных переменных равно n , а n – это общее число позиномов задачи (1) :

между задачами (1) и (2) имеется соответствие , которое сформулируем в виде теоремы :

Теорема :

1. Если задача (2) имеет оптимальное решение то и задача (1) имеет его .

2. Максимальное значение целевой функции задачи (2) равно минимальному значению целевой функции задачи (1)

3. Оптимальное решение задач (1) и (2) связаны соотношениями :

Сформулированная теорема позволяет найти оптимальное решение задачи (1) по найденному задачи (2) .

Степень трудности задачи (1)

При d=0 , решение сводится к решению системы ограничений : , , ,

При d>0 , используются другие методы ( например симплексный )

Алгоритм при d=0

1. По исходной задаче составляется двойственная функция , если без ограничений , то

2. Cоставляется система уравнений для весовых коэффициентов , , , где для задачи без ограничений и

3. Решается система и ищутся

4. Вычисляется значение двойственной функции , при найденном

5. Составляется система уравнений для задачи

- без ограничений

- с ограничениями

6. Решая полученную систему находят оптимальное решение исходной задачи , при этом

минимальное значение функции будет равно

ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ .

Методы этого типа используются для решения задач нелинейного программировании. Они основаны на построении конечной последовательности арифметических действий функций и ограничений задач нелинейного программирования .

Эти методы позволяют найти решение задачи с любой заданной точностью .

Пусть задача нелинейного программирования имеет постановку :

Различают методы :

• если ограничений нет , то задача безусловной оптимизации и соответствующие методы

• если с ограничениями , то задача условной оптимизации и соответственно методы

• одномерной оптимизации , если

• многомерной оптимизации , если

Методы одномерной безусловной оптимизации .

Предположим , что функция - унимодальная .

Определение : Функция называется унимодальной на , если существует единственная точка минимума (максимума) , а отрезок называется интервалом неопределенности .

Идея поискового метода :

В некоторой точке отрезка вычисляется , по результатам сравнения определяется точка , в которой значение функции наименьшее . Отображается т.ж. часть интервала с большим значением .

На новом интервале операция повторяется и т.д.

Перед началом поиска необходимо задать конечную длину L , которая должна быть не более ( точность ) .

Метод равномерного поиска :

• Задается начальный отрезок 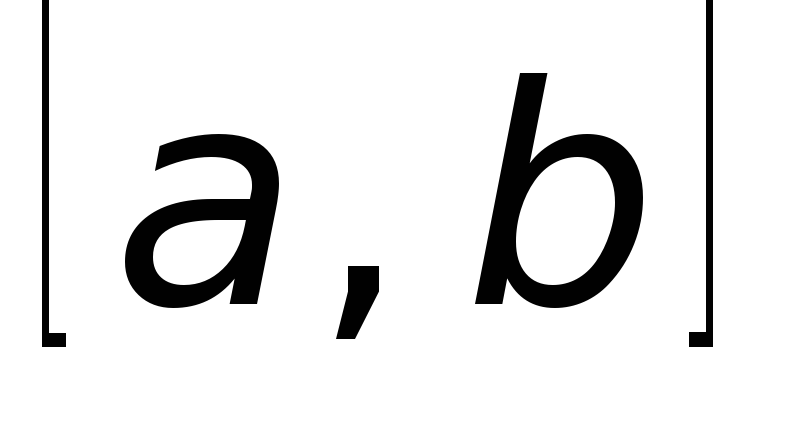, L ,

• Затем отрезок делится n равных частей , вычисляются значения _,

• Значения сравниваются и находится точка с наименьшим значением функции

• Далее интервал делится на n частей и т.д. пока L>

Метод деления на два :

Сравниваем , , . Интервал неопределенности точками ,и делится на четыре равных отрезка . Вычисляются значения функции в этих точках . Сравниваются полученные значения . В силу унимодальности функции возможны три случая :

1. следовательно выбираем отрезок

2. следовательно выбираем отрезок

3. следовательно выбираем отрезок

Т.о. интервал неопределенности сократился в двое во всех трех случаях . Далее , на следующей итерации , отрезок снова делится четыре части , но значения функции вычисляются только в двух точках , поскольку значения в трех точках уже были вычислены на предыдущей итерации . Процесс продолжается до тех пор , пока интервал не станет меньше L , т.е. , ;

Лекция 21. Численные методы условной оптимизации.

Пусть задача нелинейного программирования имеет постановку:

Методы условной оптимизации можно разделить на две группы: прямые и непрямые.

В прямых методах при решении задачи минимизации оперируют непосредственно с исходной задачей. Пример таких методов: метод проекции градиента, метод случайного поиска.

Суть этих методов состоит в том, что строится последовательность точек значение функции, на которых убывает и при этом выполняются ограничения задачи.

Непрямые методы сводят исходную задачу условной оптимизации к последовательности задач безусловной оптимизации к некоторой вспомогательной функции. В этих методах ограничения задачи учитываются в неявном виде (косвенно). Пример таких методов: метод штрафных функций.

Прямые методы. Метод случайного поиска.

В его основе лежит внесение элементов случайности в процедуру формирования точек

Задаётся начальная точка:

должна ОДР удовлетворяет всем ограничениями. Затем итерационная процедура построения этих точек.

,шаг поиска это число задаётся

элементы этой матрицы определяются:, М – положит большое число.

случайный вектор с равномерным распределением на отрезке [-1,1].

Равномерный закон распределения.

Возьмем отрезок [-1,1] и разобьём его на 10 частей. И датчиком случайных чисел сгенерировано 100 чисел.

Они будут распределены по равномерному закону . Если для всех К интервал попадет около 10 чисел (может быть 9 или 11).

Нормальный закон (1).Кривая Гауса.

В результате получаем новую точку Х₁. Для новой точки (?) случайным образом получаем новую точку.

Если процессе построения точек некоторая точка выйдет за границы области , то значение компоненты в этой точке полагается равным граничным значениям . Если на какой то итерации делается подряд неудачных попыток ( должно быть задано ), то после этого шаг поиска уменьшается в какое то количество раз и т.д.

Процедуру оптимизации прекращают, если выполняется условие , - определяет точность результата.

Метод проекции градиента.

,

Задаем начальную точку . Потом строиться последовательность точек.

- шаг спуска, - grad функции в точке Х_k.Таким образом, если точка является внутренней точкой, то это обычный градиентный метод.

Когда точка вышла за пределы области, необходимо спроектировать градиент на границу области, а дальше следующая точка ищется в направлении проекции градиента.

Определяем новую точку и т.д. Процедура заканчивается, когда

.

Сложность метода: построение проекции, если граница нелинейная.

Непрямые методы. Методы штрафных функций.

Строим вспомогательную функцию

- положительное число – коэффициент штрафа. Штраф за нарушение границы.

R – штрафная функция – она подбирается таким образом, что её значение равно нулю внутри области ОДР и резко возрастает за пределами области ОДР.