Kursovik_ed

1. Основные положения

Направляющие устройства обеспечивают движение потока энергии, переносимой электромагнитной волной, в заданном направлении. В зависимости от вида направляющих устройств в них могут распространяться электромагнитные волны разных типов: чисто поперечные или Т-волны (TEMволны), электрические или Е-волны (ТМ-волны); магнитные или Н-волны (ТЕ-волны), а также гибридные волны. На данные типы электромагнитные волны подразделяются по наличию продольных (вдоль оси направляющего устройства) компонент полей. По отношения к координате, направленной вдоль оси направляющего устройства, в Т-волнах векторы E и H имеют только поперечные составляющие; в Е-волнах вектор E имеет поперечную и продольную составляющие, а вектор H – только поперечную; в Н-волнах вектор H имеет поперечную и продольную составляющие, а вектор E – только поперечную; в гибридных волнах оба вектора имеют и продольные и поперечные составляющие.

По наличию в конструкции замкнутого проводящего экрана принято разделять направляющие устройства на открытые линии передачи и волноводы. Линии передачи, в конструкции которых имеется один или несколько проводящих экранов, ограничивающих область распространения волны, называют волноводами. По количеству изолированных проводящих поверхностей, входящих в состав конструкции направляющего устройства, различают односвязные, двухсвязные, многосвязные линии передачи и линии передачи нулевой связности. Так прямоугольный (рис. 1) и круглый (рис. 2) волноводы относят к односвязным закрытым линиям передачи, а коаксиальный волновод (рис. 3) к двухсвязным. Чисто поперечные волны могут распространяться только в двухсвязных или многосвязных линиях передачи (причем как в открытых линиях, так и в волноводах). Электрические и магнитные волны в любых линиях передачи. Гибридные волны могут существовать в неоднородных линиях передачи (заполненных неоднородной средой).

Метод изучения волновых процессов в волноводах основан на решении уравнений Гельмгольца для комплексных амплитуд электрического и магнитного полей:

2

где k ωε0εrμ0μr волновое число, диэлектрическая и магнитная проницаемости свободного пространства: ε0 # 8.85 10 12 Ф/м, P0 # 4S10 7 Гн/м; εr и Pr относительные диэлектрическая и магнитная проницаемости материала, заполняющего волновод.

b

x

а

Рис. 3. Коаксиальный волновод

3

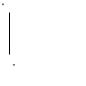
Рассмотрим для простоты случай, когда проводящие элементы волновода изготовлены из идеального проводника, тогда граничные условия имеют вид:

где L внутренняя поверхность проводящей стенки волновода; n внешняя нормаль к L.

1.1. Распространение электромагнитной волны в прямоугольном волноводе

В прямоугольном волноводе могут распространяться электрические и магнитные волны собственные моды волновода. Специфической особенностью любого закрытого волновода независимо от формы его поперечного сечения и диэлектрического заполнения, является дискретный характер спектра собственных мод, являющихся решениями уравнений Гельмгольца (1).

Найдем решение уравнений (1) при следующих граничных условиях:

где a и b поперечные размеры волновода (см. рис. 1).

Решениями уравнений являются выражения для компонент электромагнитного поля для электрических и для магнитных волн. Электрические волны:

4

единственной основной моды соответствует одномодовый режим работы волновода.

Волновод, работающий в режиме отсечки (при частотах ниже критической) для всех мод, называют запредельным волноводом.

Анализ структуры электромагнитного поля любой волны высшего типа следует начинать с преобразования системы уравнений (4) или (5) с учетом конкретных значений индексов m и n рассматриваемой волны. После этого следует изобразить картины силовых линий векторов E и H данной волны.

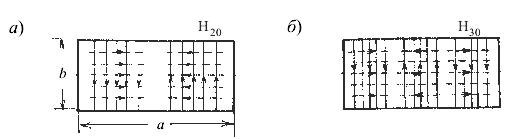
Большую помощь в решении этой задачи может оказать следующее правило. Структуру поля волны Н10 можно считать базовой при построении картин силовых линий векторов E и H собственных волн Нm0 и Н0n . Так, например, для волны Н20 картина силовых линий векторов E и H в поперечном сечении волновода получается путем двукратного воспроизведения базовой структуры вдоль широкой стенки волновода (с учетом фазовых соотношений соседних структур); для волны Н30 – трехкратным воспроизведением, и т. д. Для волны Н01 базовая структура будет повернута на угол 90°; для волны Н02 – повернута на 90° и воспроизведена дважды и т.д. (см. рис. 4).

Рис. 4. Силовые линии векторов E и H для различных типов волн: а – для волны Н20, б – для волны Н30

Несколько сложнее решается задача построения картины силовых линий векторов E и H собственных волн, у которых индексы m и n оба не равны нулю. В этом случае необходимо сначала построить картину силовых линий волны Н11 , которая затем, в зависимости от конкретных значений индексов m и n, будет воспроизводиться требуемое число раз вдоль широкой и узкой стенок волновода. Таким образом, для собственных волн типа Нmn базовой структурой является структура поля волны Н11 (рис. 5).

7

Рис. 5. Силовые линии векторов E и H для волны Н11

При построении картин силовых линий векторов E и H собственных волн Еmn базовой является структура поля собственной волны E11. Картина силовых линий векторов E и H этой волны в поперечном сечении волновода изображена на рис. 6.

Рис. 5. Силовые линии векторов E и H для волны E11

Волновое сопротивление собственных мод в прямоугольном волноводе вводится как отношение поперечных к направлению распространения волны компонент комплексных амплитуд векторов поля волны:

1.2. Распространение электромагнитной волны в круглом волноводе

Круглый волновод односвязный закрытый волновод, поперечное сечение которого имеет форму круга радиуса r (см. рис. 2). Уравнение Гельмгольца в общем виде в цилиндрической системе координат имеет вид:

где Ψ комплексная амплитуда электрического или магнитного поля.

8

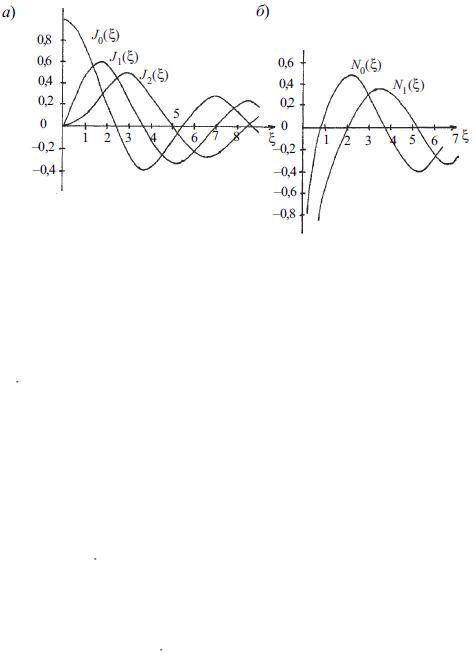
Решение уравнения (12) ищется в виде комбинации функций Бесселя первого и второго рода (функций Неймана) порядка m (см. рис. 7) по радиальной координате (r) и тригонометрических функций по угловой координате (M).

Рис. 7. Графики функций Бесселя Jm (а) и Неймана Nm (б)

В общем виде решение уравнения Гельмгольца в цилиндрической системе координат для продольной компоненты поля имеет вид:

Однако в силу условий физической задачи поле в центре волновода не может быть бесконечно большим, что навязывается значением функции Неймана при r = 0, следовательно, необходимо положить Bm = 0 в (13). Кроме того, в (13) можем опустить sin(mM). Так как начало отсчета угла M может быть выбрано произвольно, выберем за начало отсчета полуплоскость M = const, в которой Ψ z имеет максимальное значение. Косинус имеет максимальное значение при mM = 0, а синус при этом равен нулю. Перепишем (13) в соответствии с вышеизложенными соображениями:

Запишем граничные условия для электромагнитного поля на стенке волновода, выполненного из идеального проводника:

9