
Климатология 2 семестр / climat2 отчет-1
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Российский государственный гидрометеорологический университет
Кафедра МКОА
Отчёт по лабораторной работе №2:
«Применение статистических методов для оценки климатических изменений на метеостанции Марково»
Выполнил: ст. гр. Б15-ПМ-1-3
Скачков И.В.
Проверил: к.г.н., доцент каф. МКОА
Шадурский А.Е.
Санкт-Петербург 2018
Цель работы: научиться рассчитывать основные виды моделей климатических изменений (стационарная выборка, модель линейного тренда, модель ступенчатых изменений и гармоническая модель), оценивать статистическую значимость моделей и определять наиболее эффективную модель.
Расчёт для температуры: Таблица 1 Среднегодовые температуры воздуха на метеостанции Марково.
|
1895 |
17,4 |
1919 |
17 |
1943 |
17,2 |
1963 |
14 |
1983 |
13,1 |
|
1896 |
17,7 |
1920 |
16,1 |
1944 |
14,2 |
1964 |
10,3 |
1984 |
15,3 |
|
1898 |
17,7 |
1921 |
17,8 |
1945 |
14,1 |
1965 |
13,8 |
1985 |
12,4 |
|
1899 |
17,9 |
1922 |
18,4 |
1946 |
11,9 |
1966 |
14,5 |
1986 |
14,3 |
|
1900 |
18,4 |
1923 |
18 |
1947 |
10,1 |
1967 |
13,9 |
1987 |
14,2 |
|
1901 |
17,3 |
1924 |
17,8 |
1948 |
11,5 |
1968 |
15,6 |
1988 |
13,9 |
|
1902 |
18,4 |
1925 |
16,7 |
1949 |
12,4 |
1969 |
11,2 |
1989 |
10 |
|
1903 |
17,2 |
1927 |
17,7 |
1950 |
10,5 |
1970 |
14,4 |
1994 |
9,9 |
|
1904 |
18 |
1928 |
17,8 |
1951 |
13,2 |
1971 |
14,1 |
2004 |
11,3 |
|
1905 |
15,5 |
1929 |
16,8 |
1952 |
15,4 |
1972 |
15 |
2005 |
11,1 |
|
1906 |
15,4 |
1930 |
16,4 |
1953 |
15,7 |
1973 |
14,6 |
2006 |
11,1 |
|
1907 |
16,7 |
1931 |
17,2 |
1954 |
14,6 |
1974 |
13,8 |
2007 |
11,8 |
|
1908 |
18,3 |
1932 |
16,7 |
1955 |
12,7 |
1975 |
14,2 |
2008 |
10,6 |
|
1909 |
17,8 |
1933 |
18,2 |
1956 |
15,6 |
1976 |
14,6 |
2009 |
10,5 |
|
1910 |
17,3 |
1934 |
17,1 |
1957 |
13,5 |
1977 |
13,5 |
2010 |
10,8 |
|
1912 |
15,5 |
1935 |
17,1 |
1958 |
15,3 |
1978 |
13,4 |
2011 |
8,3 |
|
1915 |
16,7 |
1936 |
16,1 |
1959 |
14,4 |
1979 |
13,3 |
2012 |
9,6 |
|
1916 |
17,4 |
1937 |
15,9 |
1960 |
15,5 |
1980 |
14,4 |
2014 |
12,1 |
|
1917 |
16,4 |
1939 |
16,1 |
1961 |
14,4 |
1981 |
11,7 |
2015 |
10,4 |
|
1918 |
16,6 |
1942 |
16,6 |
1962 |
13,7 |
1982 |
14,9 |
||
Для расчёта среднегодовой температуры использовалась матрица исходных данных, и восстановленные значения на метеостанции Марково.

Рис. 1 Хронологический ход ряда среднегодовых температур на метеостанции Марково.
В ряде температуры, для статистической обработки использовались фактические и восстановленные значения.
Расчёт основных параметров временного ряда: Тср=13,0 С, Ϭ=1,945 С, дисперсия =6,44, r(1)=0,25.
Определение коэффициентов модели линейного тренда: b1 =-0,01; b0=21,14; Ϭe=1,336; Ϭ^2=1,78.

Рис. 2 Модель линейного тренда для ряда температуры.
Таблица 2. Характеристики модели линейного тренда
|
n |
b1 |
b0 |
R |
R* |
Вывод |
Ϭy |
∑e |
|
123 |
-0,01 |
21,1 |
0,23 |
0,167 |
+ |
1,375 |
1,336 |
Критическое значение R* берётся из таблицы 1 практикума. Расчетное значение меньше критического. Расчётный параметр статистически значим.
Стационарная модель характеризуется неизменностью во времени среднего значения и среднего квадратического отклонения.
Таблица 3. Характеристики ступенчатой модели
|
Годы |
Ступень |
n |
Yср |
Ϭy |
Дисперсия |
|
1886-1956 |
1 |
60 |
5,28 |
0,84 |
1,94 |
|
1957-2017 |
2 |
63 |
4,66 |
0,93 |
1,67 |
|
|
Сумма |
123 |
5,0 |
0,9 |
1,88 |

Рис. 3 Модель ступенчатых изменений ряда температуры на метеостанции Великие Луки.
На графике виден небольшой ступенчатый спад среднего значения, сопровождающийся увеличением дисперсии.
Общее
стандартное отклонение остатков
ступенчатой модели:


Рис. 4. График автокорреляционной функции временного ряда.
Наибольшие значения при периодах Т=1, 25 лет.
Таблица 4. Характеристики гармонической модели
|
n |
b1 |
b2 |
b0 |
R |
R* |
Вывод |
Ϭy |
∑eгар |
|
123 |
-0,36 |
0,52 |
4,94 |
0,18 |
0,192 |
+ |
1,375 |
1,336 |

Рис. 5 Аппроксимация моделью гармонических колебаний среднегодовой температуры воздуха на метеостанции Великие Луки.
На графике представлен временной ряд в виде суммы гармоник с периодами 1 и 25 лет, выраженные в виде регрессионного уравнения.
Таблица 5. Выбор эффективности модели
|
n |
Ϭy |
Ϭe |
Ϭeгар |
Ϭступ |
Δтр% |
Δгар% |
Δст% |
Fтр |
Fгар |
Fступ |
|
123 |
1,375 |
1,336 |
1,336 |
1,350 |
2,79 |
2,8 |
1,79 |
1,05 |
1,41 |
1,04 |
Из всех трёх моделей аппроксимация по ступенчатой модели даёт нименьшую погрешность. Все три критерия Фишера меньше критического значения, найденного в таблицы 2 практикума. Расчётные значения меньше критического, что говорит о том, что соответсвующие модели не имеют статичтически значимого различия.
Расчёт для сумм осадков: Таблица 1.1 Среднегодовые суммы осадков на метеостанции Великие Луки.
|
Год |
Uср |
Год |
Uср |
Год |
Uср |
Год |
Uср |
Год |
Uср |
Год |
Uср |
|
1886 |
53 |
1904 |
51 |
1927 |
64 |
1952 |
51 |
1970 |
48 |
1988 |
57 |
|
1887 |
49 |
1905 |
70 |
1928 |
59 |
1953 |
51 |
1971 |
42 |
1989 |
54 |
|
1888 |
37 |
1906 |
61 |
1929 |
38 |
1954 |
47 |
1972 |
44 |
1990 |
71 |
|
1889 |
30 |
1907 |
40 |
1930 |
54 |
1955 |
15 |
1973 |
42 |
1991 |
44 |
|
1890 |
48 |
1908 |
58 |
1931 |
45 |
1956 |
14 |
1974 |
48 |
1992 |
51 |
|
1891 |
53 |
1909 |
52 |
1932 |
50 |
1957 |
12 |
1975 |
50 |
1993 |
43 |
|
1892 |
56 |
1910 |
52 |
1933 |
54 |
1958 |
15 |
1976 |
48 |
1994 |
47 |
|
1893 |
34 |
1911 |
42 |
1936 |
48 |
1959 |
13 |
1977 |
60 |
1995 |
48 |
|
1894 |
51 |
1912 |
49 |
1937 |
37 |
1960 |
13 |
1978 |
67 |
1996 |
50 |
|
1895 |
52 |
1913 |
49 |
1938 |
37 |
1961 |
13 |
1979 |
50 |
1997 |
56 |
|
1896 |
40 |
1914 |
45 |
1939 |
42 |
1962 |
15 |
1980 |
46 |
1998 |
58 |
|
1897 |
31 |
1915 |
54 |
1940 |
43 |
1963 |
9 |
1981 |
58 |
1999 |
42 |
|
1898 |
44 |
1916 |
53 |
1946 |
44 |
1964 |
10 |
1982 |
40 |
2000 |
45 |
|
1899 |
58 |
1917 |
69 |
1947 |
50 |
1965 |
11 |
1983 |
47 |
2001 |
44 |
|
1900 |
61 |
1922 |
66 |
1948 |
48 |
1966 |
53 |
1984 |
56 |
2002 |
39 |
|
1901 |
54 |
1924 |
35 |
1949 |
40 |
1967 |
55 |
1985 |
60 |
2003 |
51 |
|
1902 |
81 |
1925 |
56 |
1950 |
58 |
1968 |
51 |
1986 |
55 |
2004 |
52 |
|
1903 |
70 |
1926 |
50 |
1951 |
34 |
1969 |
40 |
1987 |
69 |
|
|
Для расчёта среднегодовой суммы осадков использовалась матрица исходных данных, и восстановленные значения на метеостанции Великие Луки.

Рис. 1 Хронологический ход ряда сумм осадков на метеостанции Великие Луки.
В ряде сумм для статистической обработки использовались только фактические значения. Н графике ярко выражен провал в период 1955-1965-й года. Матрица исходных данных была проверена, действительно, на эти года приходились резкие экстремумы минимума сумм осадков.
Расчёт
основных параметров временного ряда:
Uср=46,4
мм, Ϭ=14,5 мм, дисперсия =210,5, r(1)=0,66.
Определение коэффициентов модели
линейного тренда:

Рис. 2 Модель линейного тренда для ряда сумм осадков.
Таблица 2.1 Характеристики модели линейного тренда
|
n |
b1 |
b0 |
R |
R* |
Вывод |
Ϭy |
∑e |
|
107 |
-0,04 |
128,6 |
-0,1 |
0,186 |
+ |
14,5 |
14,4 |
Критическое значение R* берётся из таблицы 1 практикума. Расчетное значение меньше критического. Расчётный параметр статистически значим.
Стационарная модель характеризуется неизменностью во времени среднего значения и среднего квадратического отклонения.
Таблица 3.1 Характеристики ступенчатой модели
|
Годы |
Ступень |
n |
Yср |
Ϭy |
Дисперсия |
|
1886-1957 |
1 |
60 |
48,16 |
9,23 |
165,4 |
|
1958-2004 |
2 |
48 |
44,27 |
11,36 |
264,5 |
|
|
Сумма |
108 |
46,4 |
14,51 |
210,6 |
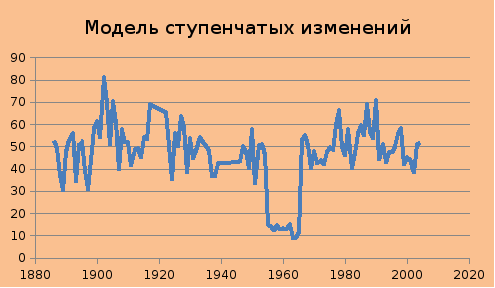
Рис. 3 Модель ступенчатых изменений ряда сумм осадков на метеостанции Великие Луки.
На графике виден небольшой ступенчатый спад среднего значения, сопровождающийся увеличением дисперсии.
Общее
стандартное отклонение остатков
ступенчатой модели:


Рис. 4. График автокорреляционной функции временного ряда.
Наибольшие значения при периодах Т=1, 29. Таблица 4. Характеристики гармонической модели
|
n |
b1 |
b2 |
b0 |
R |
R* |
Вывод |
Ϭy |
∑eгар |
|
108 |
-2,22 |
-0,18 |
46,43 |
0,08 |
0,185 |
+ |
14,51 |
14,43 |

Рис. 5 Аппроксимация моделью гармонических колебаний сумм осадков на метеостанции Великие Луки.
