1. \\Понятие множеств. Числовые мн-ва.

Мн-ва-совокупнсть объектов одной природы,объед между собой по какому-л характерному признаку и обзнач больш лат буквой.

Для графич изобр мн-в исп диагр Эйлера-Вьенна.

Мн-во А наз конеч мн-вом,если оно сост из конеч числа элем.В этом случае мн-во мб задано простым перечисл его элем: А= {1,2,3}

Если число элем мн-ва бесконечно,то его наз бесконечным мн-вом.

Если мн-во не содержит ни 1 эл, его наз пустым.ᴓ

Эл мн-ва мб заданы в виде логич усл А={х:|x|<1}

Любое конечное мн-во явл счетным. Бесконеч мн-во явл счетным,если элем данного мн-ва можно сопоставить рядом натур чисел.

Над мн-вами м выполн след операции:

1.объединение(сложение). Суммой 2х мн-в А и В наз мн С=А+В=АᴜВ,кот сост как из элем мн А так и мн В.Операция сложения в мат лог соотв операции дизъюнкция «или»

2. пересечение(произведение). С=АВ=А ᴧВ. С сост из общих элем мн-в А и В. В мат лог соотв конъюнкции.

Числовые мн-мн,которые сост из чисел. Мн нат чисел N={1,2..}

Мн целых ч: Z={-1,0,1}

Рац ч: Q={дроби}

Иррац(трансценд): {π е корни}

Для числ мн справедливо: NʗZʗQʗRʗC

2. Комплексные числа.Различные формы записи

КЧ-число z=x+iy (алг фз), где х-действ часть,а у –мнимая. Число i-мнимая ед.= -1, i²=-1. При х=0, число z назыв чисто мнимым, а при у=0 ч z явл R(действ).

Для изобр КЧ исп декарт сист коорд.,где оси ОХ отклад действ часть,по ОУ-мним.

Модулем КЧ z назыв длину или модуль радиус вектора точки z:

|z|=|

Аргументом кч z наз величину угла ϕ+2πk ,где угол ϕ – угол между полож направлением Охи радиус-вектором z .При к=0 знач arg счит главным знач.(argz=ф)

Тогда тригоном фз: z=|z|(cosф+isinф)

Если ϕ изменяется от 0 до 2π, то для его вычисл удобно использ:

ϕ = arctg|y/x|, 1 четв

П-arctg|y/x|, 2 четв

П+ arctg|y/x|, 3 ч

2п- arctg|y/x|, 4 ч

Показат фз: z=|z|e^iф

3. Операции над КЧ

1. Сумма 2 чисел z₁ и z₂: z=z₁+z₂=(x₁+x₂)+i(y₁+y₂)

2. Умножение кч на действительное ч: каждое из его дейст и мним частей умнож на это число. При умнож на отр ч радиус-вектор исходного ч поворачивается на п радиан.

3. Деление:

Алгебр фз: =

Тригоном фз:

Показат фз:

4. Произведение

Алгебр фз: х1х2-у1у2+i(y1x2+x1y2)

Тригоном фз: |z₁||z₂|(cos(ф1+ф2)+isin(ф1+ф2)

Показат фз: |z₁||z₂|e^i(ф1+ф2)

5. Возв в нат степень: zⁿ=|z|ⁿ(cosnф+isin nф)

4. Извлечение корня из комплексного числа

z=|z|(cosф+isinф)

найдем все значения ω, ω=

Пусть ω= | ω |*(cosθ+isinθ), z= |z|(cosф+isinф), значит ωⁿ=z

По формуле Муавр | ω |*(cosθ+isinθ)= |z|(cosф+isinф) |ω|ⁿ=|z|, n θ= π+2πk

Из формулы видно, что нат корень комплексного числа имеет ровно n рзличных значений. При извлечении заменяем (-1) на i ² .

Изображение полученного значения корня в компл плоскости:

Замечание: из ф-лы извлечения корня комплексного числа следует, что все корни в комплексн. пл-ти лежат в вершине правильного n-угольника, который вписан в окружность R= , причем перв вершина определ arg ω₀=

5. Понятие ф-и и способы ее задания.

Ф назыв отображение мн-ва Х на мн-во У. f:X->Y, при котором каждому хсХ ставится единственный элемент мн-ва У. х-обл опред f, у-обл значений.

Обратной ф к f назыв отобр, мн. У на мн. Х, при кот каждому эл мн-ва У ставится в соотв единств элем мн. Х. f^-1:Y->X. Не каждая ф-я имеет обратную. Чтобы ф-я имела обратную, отобр f должно быть взаимно однозначным. D(y) обр ф-и =Е(у) самой ф-и.

Если в кач-ве мн Х и У рассм числовые мн-ва,то ф-ю назыв числовой. y=f(x)

Способы задания:

1 табличный

2 графический

3 аналитич (алгебр ур-е)

Х²+2у=1 *

Если ур-е разрешено относит у, то ф-я – явно заданная. При явном задании значение у вычисляется непосредственно.

Если ф-я *, то ф-я задана неявно.

Любую явно зад м запис в виде неявной. Но не всякую неявно зад м сделать явно зад.

6. Осн хар-ки ф-й.

1. Монотонность

y=f(x) наз возрастающ(строго в),если для люб х₁>x₂=> f(x₁)>F(x₂)

y=f(x) –убыв, если х₁>x₂=> f(x₁)<F(x₂)

y=f(x)-монотонная,если она либо (строго)возр, либо (стр)убыв.

2. Периодичность

f(x) пер,если f(x+Т)= f(x), Т>0. При этом если Т явл наим из всех чисел,для которых справедливо данное равенство, то Т-период ф. sin(x+8п)=sinx, T=2п.

3. Четность

У=f(x) четн,если f(-x)=f(x).Гр чет ф симм относит ОУ. У=х²

f(x)-нечет,если f(-x)=-f(x). У=sinx

4. Ограниченность

- f(x) огранич сверху,если сущ число М: Vx=> f(x)≤M

- f(x) огр снизу. Если сущ m: Vx=> f(x)≥m

- f(x) огр (св и снизу), если m и М: Vx=>m≤ f(x)≤M

5. Наиб знач ф-и f(x) наз число М: Vx=> f(x)≤M, причем сущ х₀: f(x₀)=M.

Если х₀нет то f(x) не имеет наиб знач,хотя и явл ограниченной (arctgx)

6. Наим знач ф назыв число m: Vx=> f(x)≥m, причем сущ х₀: f(x₀)=m. Если х₀нет, то f(x) не имеет

наим знач.

7. Точной верхней границей для f(x) назыв число М: Vx=> f(x)≤M, где М-наим из всех чисел,для

кот справедливо данное неравенство: M=supf(x)

8. Точной нижней границей для f(x) назыв m: Vx=> f(x)≥m, где м –наиб из всех чисел для кот

справедливо m=inf f(x)

Замечание: если f(x) имеет наиб/наим знач, то эти знач совпад с верх и нижн гранями.

7. 7. Построение графиков функций путем их преобразования.

Пусть известен гр. у= f(x), тогда можно построить след. Графики

1) y=f(x-a), который получается путем параллельного переноса гр. f(x) на а единиц вправоб при а>0 и влево при a<0.

2) y=f(x)+b, кот. Получ. Путем парал.переноса из гр. f(x) при b>0 вверх и при b<0 вниз.

3) y=f(kx), кот. получ. Из исходного f(x) путем сжатия в К-раз (К>1) – вдоль оси ОХ и путем растяжения в 1/К-раз при 0<k<1.

Замечание. Если k<0, то сначала строим гр. ф-ии y=f(-x), кот. получ. Из исходного путем зеркального отображения его относит. Оси ОУ.

4) y=k*f(x), кот. получ. путем растяжения его в k-раз при k>1 вдоль оси OY и путем сжатия 1/к-раз при 0<k<1 вдоль ОУ.

если k<0, то сначала строим y=-f(x), кот. получ. из исходного путем зеркального отображения его относит. Оси ОХ.

Алгоритм. y=c*f(kx-a)+b

1) y=f(x)

2) f(kx-a)=f(k(x-a\k)) y=f(kx)

3) y=f(k(x-a\k)), кот. получ. путем параллельного движения вдоль второго графика вдоль оси ОХ на a\k-единиц.

4) y=c* f(k(x-a\k))

5) y=c* f(k(x-a\k))+b

График, где ф-я с модулем.

y=f(|x|)

1) строим f(x) при x>=0 и зеркально отображаем относ. ОУ.

2) y=|f(x)| - зеркально отображаем отрицательные значения f(x) относ. ОХ.

3) для построения линии , в уравнениях которых есть |y|=f(x) строят гр. f(x) для всех х, при кот. f(x)>=0 и затем полученный гр. зеркально отображают относительно ОХ.

выражение |y|=f(x) не является функцией.

Построение гр. обратных функций.

1) строим гр. y=f(x)

2) строим прямую y=x, тогда y=f(-1)(x) строится путем зеркального отображения относительно прямой y=х(является осью симметрии прямого и обратного графиков)

Замечание.

1. если f(x) не является монотонной на всей числовой прямой, то для определения обратной функции выбирают промежутки x, где она является монотонной и на этих пром-ках строится обратная функция.

2. Область опред. обратной ф-ии совпадает с обл. значения самой функции.

8. Основные элементарные функции и их графики.

1) Показательная функция y=ax

Свойства: a>1 a<1

а) Область определения: D(f)=R

б) Область значений: E(f)= (0;+бескон)

в) Промежуток возрастания: при а>1(R); a<1 нет.

г) Промежутки убывания: a>1 нет; при а<1(R)

д) Нули функции: нет

е) Промежутки знакопостоянства:

y>0 если X є (R)

y<0, нет таких Х

2)Степенная

Степенными называют функции вида xα, где α может быть целым, дробным, положительным или отрицательным. К ним относятся всем знакомая линейная функция y = kx + b, квадратичная парабола y = x2(в общем виде: y = ax2 + bx + c),кубическая парабола y = x3. Степенными являются также гипербола y = 1/x, которую можно представить как y = x−1, функция y =√x и др.

Четная степень

у=х²

1. D(x)=R – функция определена на все числовой оси;

2. E(y)=[0;∞) - функция принимает положительные значения на всей области определения;

3. При х=0 у=0 - функция проходит через начало координат O(0;0).

4. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).

5. Функция является четной (симметрична относительно оси Оу).

В зависимости от числового множителя, стоящего перед х², функция может быть уже/шире и направлена вверх/вниз.

Нечетная степень

у=х³

1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:

2. D(x)=R – функция определена на все числовой оси;

3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;

4. При х=0 у=0 – функция проходит через начало координат O(0;0).

5. Функция возрастает на всей области определения.

6. Функция является нечетной (симметрична относительно начала координат).

В зависимости от числового множителя, стоящего перед х³, функция может быть крутой/пологой и возрастать/убывать.

целый отрицательный показатель:

Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:

1. D(x)=(-∞;0)U(0;∞) для любого n;

2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;

3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.

4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.

5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

Дробный показатель

Степенная функция с дробным показателем степени обладает следующими свойствами:

1. D(x) =R, если n – нечетное число и D(x)=[0;∞), если n – четное число ;

2. E(y) =(-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число;

3. Функция возрастает на всей области определения для любого числа n.

4. Функция проходит через начало координат в любом случае.

Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.

Основные характеристики и свойства логарифмической функции:

- область определения функции: x > 0, а область значений: - < y < +

( т.e. y R );

- это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1;

- функция неограниченная, всюду непрерывная, непериодическая;

- у функции есть один ноль: x = 1.

Тригонометрические функции.

При построении мы используем радианную меру измерения углов. Тогда функция y = sin x представляется графиком. Эта кривая называется синусоидой.

График функции y = cos x ; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на /2.

Из этих графиков очевидны характеристики и свойства этих функций:

- область определения: - беск < x < + беск ; область значений: -1<= y<=+1;

- эти функции периодические: их период 2π;

- функции ограниченные ( | y |<=1 ), всюду непрерывные, не монотонные, но

имеющие так называемые интервалы монотонности, внутри которых они

ведут себя, как монотонные функции

- функции имеют бесчисленное множество нулей

Графики функций y = tan x и y = cot x показаны соответственно на рис

Из графиков видно, что эти функции: периодические ( их период ,

неограниченные, в целом не монотонные, но имеют интервалы монотонности, разрывные. Область определения и область значений этих функций:

Обратные тригонометрические функции.

Функции y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х) называют обратными тригонометрическими функциями.

Функция y= arcsin(x):

Свойства функции y = arcsin (x):

1. Область определения D(x)=[−1;1]

2. Область значения E(y)= [−π/2;π/2]

3. y=arcsin(x)- непрерывная строговозрастающая функция на D

5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x

6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х)

Функция y= arccos(x):

Свойства функции y = arccos (x):

1. Область определения D(x)=[−1;1]

2. Область значения E(y)= [0;π]

3. y=arccos(x)- непрерывная строговозрастающая функция на D

5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x

6. y=arccos(x) функция общего вида

Функция y=arctg(x):

Свойства функции y = arctg (x):

1. Область определения D(x)=(- ∞;+∞)

2. Область значения E(y)Î=[−π/2;π/2]

3. y=arctg (x)- непрерывная строговозрастающая функция на D

4. График y = arctg(x) симметричен графику y = tg(x) относительно линии y=x

5. y=arctg (x) нечетная функция.

Функция y= arcсtg(x):

Свойства функции y = arcсtg (x):

1. Область определения D(x)=(- ∞;+∞)

2. Область значения E(y)= [0 ; π]

3. y=arctg (x)- непрерывная строгоубывающая функция на D

4. График y = arcсtg(x) симметричен графику y = сtg(x) относительно линии y=x

5. y=arcctg (x) функция общего вида.

9.Предел числовой последовательности и его геометрический смысл.

Пределом числ. посл-ти xn, когда n∞, называют число А:для люб. ε>0 существ. N: n>N =>|xn-A|<ε

lim(n->∞)xn = A

Геометрически это означает, что для любой ε-окрестности т.А найдется номер числовой послед-ти, начиная с которого все оставшиеся члены будут попадать в ε-окрестность т.А.

Окрестность т.А – любой интервал, содержащий данную точку на числовой прямой.

ε-окр-ть точки А – интервал (А-ε; А+ε)

В определении пределов числ. послед-ти число А является точкой сгущения членов числовой послед-ти на числовой оси.

10. Свойства пределов числовых последовательностей.

Рассмотрим последовательности { }{ }{ }

1. 

2. 

3. 

4. 

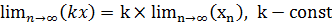
5. Пусть для членов последовательности и начиная с некоторого номера N и для всех оставшихся членов вып неравенство ≤

6. Пусть , начиная с некоторого номера N и для всех оставшихся номеров последовательности { }{ }{ } выполняется:

7. Признак существования предела. Если предел числовой последовательности существует, то он является единственным.

10. Признак Вейер Штраса и число е

Всякая монотонная ограниченная последовательность имеет предел.

В качестве примера на применение этого признака рассмотрим последовательность.

По формуле бинома Ньютона

Из равенства (15.3) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 1/n — убывает, поэтому величины (1-1/n), (1-1/n), ... возрастают.

Поэтому последовательность {х_n} = { (1+1/n)ⁿ }— возрастающая, при этом

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства (15.3) на единицу; правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменив числа 3, 4, 5,..., стоящие в знаменателях дробей, числом 2:

Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:

Поэтому

Итак, последовательность ограничена, при этом для n є N выполняются неравенства (15.4) и (15.5):

Следовательно, на основании теоремы Вейерштрасса последовательность имеет предел, обозначаемый обычно буквой е:

Число е называют неперовым числом. Число е иррациональное, его приближенное значение зэавно 2,72 {е=2,718281828459045..). Число е принято за основание натуральных логарифмов: логарифм по основанию е называется натуральным логарифмом и обозначается ln(x), т. е. Ln(x)=log_ex. Найдем связь между натуральным и десятичным логарифмами. По определению логарифма имеем х=е^ln(x). Прологарифмируем обе части равенства по основанию 10:

Пользуясь десятичными  логарифмами,  находим  lge ≈ 0,4343.   Значит, lgx ≈ 0,4343•ln(х). Из этой формулы следует, что ln(x) ≈ 1/0.4343 lg(x),  т. е. Ln(х) ≈ 2,3026 lgx. Полученные формулы дают связь между натуральными и десятичными логарифмами.

10. Предел функции в точке и его геометрический смысл

Пусть функция у=ƒ (х) определена в некоторой окрестности точки х_о, кроме, быть может, самой точки х_о.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x₀ (или при х х_о), если для любой последовательности допустимых значений аргумента x_n, n є N (x_nx₀), сходящейся к х_опоследовательность соответствующих значений функции ƒ(х_n), n є N, сходится к числу А

В этом случае пишут        или ƒ(х)—>А при х→х_о. Геометрический смысл предела функции:  означает, что для всех точек х, достаточно близких к точке х_о, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все хх_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.

Геометрический смысл предела функции:

если для любой ε-окрестности точки А найдется такая δ-окрестность точки х_о, что для всех ххо из етой  δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

10. Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

14. Неопределённость

Для раскрытия этой неопределённости нужно выделить в числителе и знаменателе выражения, которые обращают их в 0. Затем сохранить получившееся выражение и вычислить предел по обычным правилам. Для этого числитель и знаменатель раскладывают на множители.

Для раскрытия неопределенности этого вида, когда выражение под знаком предела содержит тригонометрические формулы, используют также ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ: lim =1

x 0

15. неопределённость  

Для раскрытия этого вида неопределённости используют ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ: lim (1+ ) =e

x

Другая форма записи: lim (1+x) =e

x 0

16.Сравнение бесконечно малых функций. Пример эквивалентных функций

Сравнение бесконечно малых функций

Рассмотрим окрестности в точки две бесконечно малые функции α=α(х) и β=β(х) – для этих функций в окрестности точки справедливо следующие понятия:

1.Функция α(х) является бесконечно малой функций более высокого порядка если предел этой точки равен 0, а β называют более низкого порядка по отношению α(х)

2.Функции α(х) и β(х) в точке называют бесконечно малыми функциями одного порядка если ; с- const, c 0

3.Функция α(х) и β(х) в окрестности точки называют эквивалентными функциями если пределы отношений в этой точке равен 1. ; α(х) β(х)

Примеры эквивалентных функций

1. sinx x,

2. tgx x* =0 tg0,01 0,01

3. 1-cosx докажем

4.

Ln(1+x) x докажем

17.Непрерывность функции в точке

Функция y=f(x) называется непрерывна в точке если значение функции в этой точке совпадает с ее пределами. - обозначает следующее:

1.(смотрят на правую часть равенства) функция y=f(x) в точке существует

2.(левая часть равенства) предел функции в точке существует это означает что односторонние пределы в этой точке функции равны

3.Предел и значение в точке совпадает

Определение непрерывности функции в точке

Приращение функции y=f(x) в точке называют . =f( + )- f , =x- , есть приращение независимой переменной х, а точка х принадлежит окрестности точки . Функция y=f(x) называется непрерывной в точке если выполняется

Замечание: 1 и 2 определение непрерывности функции эквивалентны между собой

18.Свойства непрерывных функций

1.Приумножение непрерывной функции на постоянную величину получаем непрерывную функцию

2.Сумма двух непрерывных функций есть непрерывная функция

3.Произведение двух непрерывных функций есть непрерывная функция

4.Частное двух функций есть такая непрерывная функция в области своего определения.

5.Если функция y=f(x) на отрезке [A;B] непрерывна причем на концах этого отрезка применяет значение равных знаков, то внутри данного отрезка найдется одна точка в которой функция обращается в 0.

6.Если функция f(x) непрерывна и монотонна и на концах этого отрезка принимает значение разных знаков, то существует единственная точка в которой функция обращается в 0

7.Если функция y=f(x) на отрезки АВ непрерывна, то на этом отрезке достигает своего наименьшего и наибольшего значения. При чем все значения функции будут удовлетворять m f(x) M, где m – наименьшее значение, M – наибольшее значение

8.Если функция y=f(x) на отрезке АВ непрерывна и монотонна, то наименьшее и наибольшее значение будет принимать на концах отрезка, если она возрастает наименьшее – в левом конце, а наибольшее – в правом конце и если убывает то наоборот

9.Все элементарные функции в области своего определения являются непрерывными функциями.