11.2. Случайные величины, функции и стохастические процессы

Величина, которая может принимать различные значения в результате опыта, называется случайной величиной. Чтобы задать такую величину нужно указать все возможные ее значения и поставить им в соответствие вероятности, с которыми случайная величина принимает эти значения.

Функцией распределения случайной величины называется функция F(x) равная вероятности P события состоящего в том, что она принимает значение превышающие х, т.е.

, где – все значения числовой оси.

Функция распределения непрерывной случайной величины показана на рис. 111.

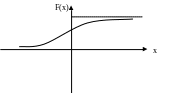
Рис. 111. График случайной величины

Производную называют плотностью распределения случайной величины.

Ее физический смысл –

Свойства

Н а рис. 112 показан один из возможных графиков плотности вероятности.

Рис. 112. График плотности вероятностей

Функция, значения которой при каждом значении независимой переменной являются случайной величиной, называют случайной функцией. Случайные функции для которых независимой переменной является время называют стохастическими процессами. Регистрацию случайной функции в той или иной форме называют реализацией случайной функции.

Если при исследовании случайного процесса располагать некоторой совокупностью реализаций, то при фиксированном значении можно определить совокупность случайных величин и плотность распределения .

Сечения ансамбля реализаций, при ряде значений дают -мерную величину, для которой можно определить многомерную функцию плотности распределения .

Рис. 113. Случайный процесс (совокупность отдельных реализаций)

11.3. Характеристики случайных процессов

Математическое ожидание случайного процесса

определяет среднее значение случайного процесса и геометрически соответствует центру тяжести плотности распределения случайной величины (момент 1-го порядка).

Корреляционная функция, или момент второго порядка,

определяет среднее значение произведения 2–х случайных функций. Они характеризуют степень зависимости между ними.

Моменты более высоких порядков обычно не определяются, и теория стохастических процессов изучающая свойства по 2-м первым моментам, называется корреляционной теорией случайных функций.

Центрированная, или несмешанная, корреляционная функция

(139)

Дисперсия

. (140)

Взаимная корреляционная функция

. (141)

Центрированная взаимокорреляционная функция

. (142)

Случайный процесс (t) называется стационарным, если

. (143)

и корреляционная функция зависит только от разности аргументов, т.е.

(144)

Среднее значение по времени

. (145)

Эргодическим называется стационарный процесс, у которого

. (146)

Среднее по времени равно среднему по совокупности реализаций при достаточно большом T для любой реализации эргодического случайного процесса.

Статистические свойства эргодического процесса могут быть определены по одной единственной реализации за достаточно большой промежуток времени.

Корреляционная функция эргодического стационарного процесса

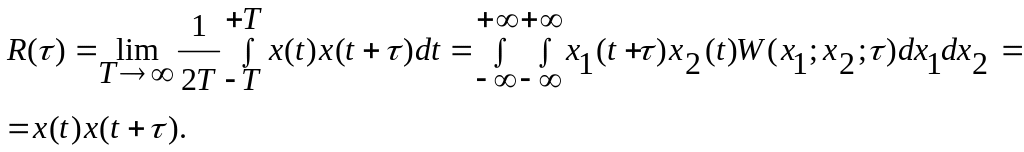Физический смысл корреляционной функции состоит в следующем: корреляционная функция характеризует связь между (t) и (t + ). Если  мало по сравнению с постоянной времени, то связь велика и R(t) достигает максимума. Это говорит о том, что близко стоящие значения (t) и (t +) мало отличаются.

Корреляционная функция имеет следующие свойства:

1. R(t) при (t) = 0 стремится к 0 при   :

;

2. Начальное значение R(0) равно среднему значению квадрата и поэтому положительно

- дисперсия;

3. R() = R(-) – четная функция;

4. Всегда R(0) > R().

Примеры корреляционных функций

1. Белый шум – абсолютно случайный процесс, у которого нет какой-либо связи между предыдущим и последующим значением x(t): R() = ().

Рис. 114. Корреляционная функция

2. Если x(t) содержит постоянную составляющую, то



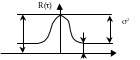
τ

Рис. 115. Корреляционная функция с постоянной составляющей

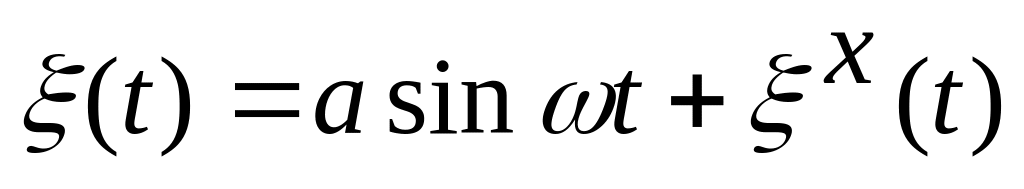3. Если , то

R()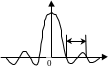



Рис. 116. Центрированая корреляционная функция

4. Если R() не содержит постоянной и переменной составляющих, то ее вид следующий

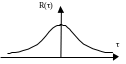
Рис. 117. Типичная корреляционная функция

Схематически вычисление корреляционной функции показано на рис. 118.

Рис. 118. Структурная схема вычисления корреляционной функции

Спектральная плотность S() определяется как преобразование Фурье корреляционной функции

. (147)

Обратное преобразование Фурье определяет

. (148)

При  = 0; m_x = 0 получаем

, (149)

т.е. дисперсия пропорциональна площади спектральной плотности.

Спектральная плотность может быть представлена иным способом. Введем финитную функцию

(150)

Преобразование Фурье определяет частотную (спектральную) функцию:

. (151)

По формуле обратного преобразования

. (152)

Определим дисперсию левой и правой частей выражения

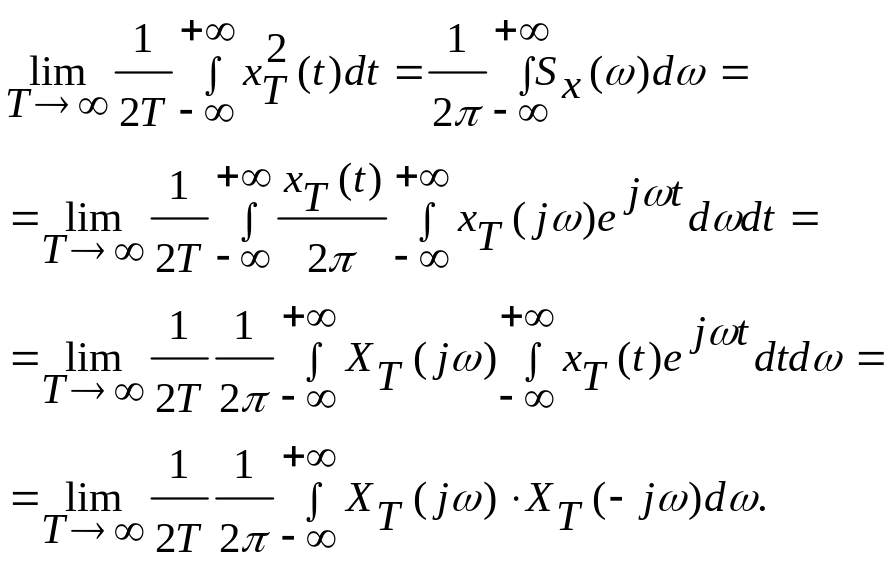(153)

Сравнивая выражения в левой и правой частях, находим

(154)

Взаимная спектральная плотность

(155)

Спектральная плотность характеризуется следующими свойствами:

1. S_x() = S_x(-). Функция спектральной плотности – действительно четная функция.

2. Спектральная плотность белого шума представляет равномерное распределение (рис. 119).

Рис. 119. График спектральной плотности «белого шума»

3. Если случайный процесс имеет постоянную составляющую, то S() содержит  - импульс в начале координат.

S()



Рис. 120. График спектральной плотности заданного процесса  - функциями

4. Е сли случайный процесс содержит гармоническую составляющую с частотой ₀, то S() содержит пики на частотах ₀ и -₀ (рис. 121).

Рис. 121. Спектральная плотность с двумя смещенными

5. Если x(t) не имеет постоянной и гармонических составляющих, то S() имеет вид гладкой функции (рис. 122).

S()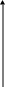



Рис. 122. График спектральной плотности типового входного сигнала