
- •Свойства определителей
- •Системы линейных уравнений
- •Решение слау.
- •Действия над матрицами.
- •6) Линейные действия над векторами. Опр. Коллинеарности и компланарности векторов.
- •7) Исследование линейной зависимость векторов на плоскости и в пространстве.
- •8) Определение базиса векторов и координат вектора. Прямоугольная система координат.
- •9) Проекция вектора на ось. Координаты точки и вектора в прямоугольной системе.
- •10) Линейные действия над векторами в координатном представлении.
- •14) Вывод уравнения окружности
- •21) Полярная система координат.
- •22) Общее уравнение кривой второго порядка. Переход к каноническим уравнениям
- •24) Угол между плоскостями. Расстояние от точки до плоскости
- •25) Вывод канонического и общего уравнения прямой в пространстве. Переход между ними
- •26. . Элементы теории множеств
- •Символика математической логики
- •Определение функции в теории множеств
- •27. Общие свойства функций
- •28. Элементарные функции
- •29. Числовые последовательности
- •30. Бесконечно малые и бесконечно большие функции
- •36) Общие правила раскрытия неопределенностей
- •37) Опр. Средней скорости движения, мгновенной скорости, производной от функции. Алгебраический, физический, геометрический смысл производной.
- •40) Производные высших порядков. Дифференциалы высших порядков.
Решение слау.
Решим
систему

Перепишем её в матричном виде:
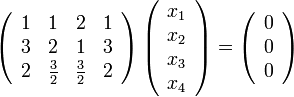
Путём
элементарных преобразований над строками
приведём её основную матрицу к ступенчатому
виду:
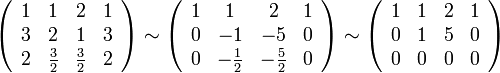
Таким
образом ранг системы (ранг её основной
матрицы) равен двум. Это значит, что
существует
![]() линейно независимых решения системы.
линейно независимых решения системы.
Перепишем
полученную систему в виде уравнений:
![]()
Возьмём
и в качестве главных переменных. Тогда:
![]()
Подставим
по очереди единицы в качестве одной из
свободных переменных:
![]() и
и
![]() .
.
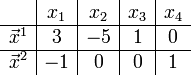
Тогда
общее решение рассматриваемой системы
может быть записано так:
![]()
а
вектора
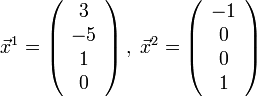 составляют фундаментальную систему
решений.
составляют фундаментальную систему
решений.
Формулы Крамера
Метод Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы.
Система
линейных уравнений:
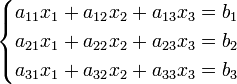
Определители:


Решение:
![]()
Пример:
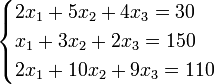
Определители:
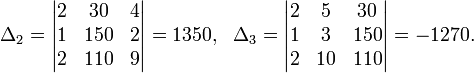

![]()
Метод Гаусса.
Покажем, как методом Гаусса можно решить следующую систему:
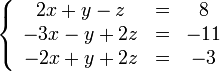
Обнулим
коэффициенты при во второй и третьей
строчках. Для этого вычтем из них первую
строчку, умноженную на
![]() и
и
![]() ,
соответственно:
,
соответственно:
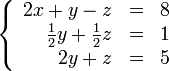
Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на 4:
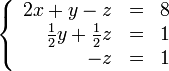
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
![]() из
третьего;
из
третьего;
![]() из
второго, подставив полученное Z
из
второго, подставив полученное Z
![]() из
первого, подставив полученные
Z и X.
из
первого, подставив полученные
Z и X.
Действия над матрицами.
Сумма двух матриц:

Произведением числа m на матрицу:
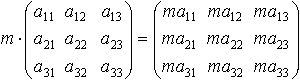
Произведение AX:
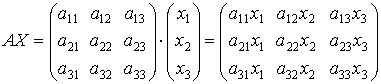
Произведение двух матриц A и B:
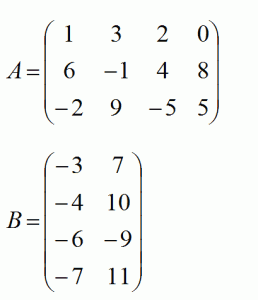
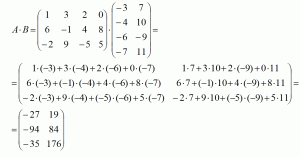
Матричный метод решения систем линейных уравнений.
Пусть дана система уравнений:
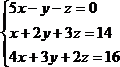 Х
=
Х
=
![]() ,
B =
,
B =
![]() , A =
, A =

Найдем обратную матрицу А(-1)
D
= det A =
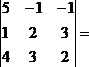 = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
= 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
M11
=
![]() = -5; M12 =
= -5; M12 =
![]() = 1; M13 =
= 1; M13 =
![]() = -1;
= -1;
M21
=
![]() M22 =
M22 =
![]() M23 =
M23 =
![]()
M31
=
![]() M32 =
M32 =
![]() M33 =
M33 =
![]()
Далее:
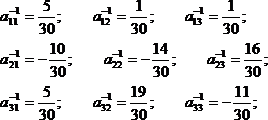 A(-1)
=
A(-1)
=

Cделаем проверку: A*(A-1) =

Находим матрицу Х.
Х
=
= (А-1)*В =
=
=

Итого решения системы: x =1; y = 2; z = 3.
6) Линейные действия над векторами. Опр. Коллинеарности и компланарности векторов.
Коллинеарные - два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой.
Компланарные - три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.
Линейные действия над векторами – сложение, умножение на число.
Сложение
-
Пусть даны два вектора ![]() и
и ![]() .
Приложим вектор
к
некоторой точке O,
получим
.
Приложим вектор
к
некоторой точке O,
получим ![]() .
Приложим вектор
к
точке A,
получим
.
Приложим вектор
к
точке A,
получим ![]() .
Тогда вектор
.
Тогда вектор ![]() будем
называть суммой векторов:
будем
называть суммой векторов: ![]() .
.
Умножение на число - Произведением вектора на число k называется вектор, который:
коллинеарен вектору ;
сонаправлен ему, если k > 0, или противоположнонаправлен, если k < 0;
длины связаны следующим соотношением:

