23 Билет

Базис и размерность векторного пространства.Свойства размерности векторного пространства.Изоморфизм векторных пространств.

Линейное пространство R называется n-мерным если в нем существует n линейно независимых векторов, а любые из (n+1) векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число n называется размерностью пространства R и обозначается dim (R)

Совокупность n линейно независимых векторов n-мерного пространства R называется базисом.

Векторные пространства V1 и V2 называются изоморфными, если между векторами этих пространств можно установить взаимнооднозначное отображение f, сохраняющие операции. Т.о. векторные пространства V1 и V2 изоморфны, если:

1. (Ах, у?V1) (x не равно у равносильно f(x) не равно f(y))

2. (Ах, у?V1) (f(x+y) = f(x)+f(y))

3. (Ax?V1) (A лямбда ? R) (f(лямбда х)=лямбда f(x))

Отображение удовлетворяющее этим условиям называется изоморфизмом.

Утверждение: Любые 2 вектор. Пространства одинаковой размерности изоморфны.

24 Билет

Подпространство линейного пространства.Сумма и пересечение подпространств.Прямая сумма подпространств.

Множество называется подпространством линейного пространства V, если:

1. 

2. 

Мы введем сейчас операции, которые позволяют из данных подпространств некоторого линейного пространства L строить новые подпространства. Пусть L1 и L2 – подпространства в L.

Суммой подпространств L1 и L2 называют подмножество в пространстве L, состоящие из векторов х1+х2, х1? L1, х2? L2:

L1+L2={х1+х2| х1? L1, х2? L2}

Пересечением L1 ^ L2 подпространств L1 и L2 называются их теоретико-множественное пересечение, т.е. множество: L1 ^ L2={х|х? L1 и х? L2}

Сумма L1+L2 называется прямой, если для любой х? L1+L2 можно представить в виде х=х1+х2, где х1?L1, x2?L2 единственным образом. Обозначается L1+L2.(над иксами черточки и плюс в кружочке)

25 Билет

Линейная оболочка системы векторов. Теоремы о базисе и размерности линейной оболочки.

Пусть - система векторов из векторного пространства V над полем P.

Определение 2: Линейной оболочкой L системы A называется множество всех линейных комбинаций векторов системы A. Обозначение L(A).

Можно показать, что для любых двух систем A и B,

1. A линейно выражается через B тогда и только тогда, когда (1)

2. A эквивалентна B тогда и только тогда, когда L(A)=L(B). (2)

Доказательство следует из предыдущего свойства

3. Линейная оболочка любой системы векторов является подпространством пространства V.

Доказательство

Возьмём любые два вектора х и у из L(A) имеющие следующие разложения по векторам из A:

Проверим выполнимость условий 1) и 2) критерия:

1. так как представляет собой линейную комбинацию векторов системы A.

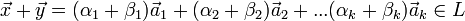2. так как тоже представляет собой линейную комбинацию векторов системы A.

Рассмотрим теперь матрицу Линейная оболочка строк матрицы A называется строчечным пространством матрицы и обозначается Lr(A). Линейная оболочка столбцов матрицы A называется столбцовым пространством и обозначается Lc(A). Обратите внимание, что при строчечное и столбцовое пространство матрицы A являются подпространствами разных арифметических пространств Pn и Pm соответственно. Пользуясь утверждением (2), можно придти к следующему выводу:

Теорема 3: Если одна матрица получена из другой цепочкой элементарных преобразований, то строчечные пространства таких матриц совпадают.

Теорема. Размерность ЛО L(X1,X2...Xn) векторов (X1,X2...Xn) равна максимальному числу линейнонезависимых векторов в системе векторов (X1,X2...Xn). В частности если все векторы (X1,X2...Xn) линейнонезависимы, то размерность ЛО равна числу векторов, а сами эти векторы образуют базис