10. Определитель произведения матриц

Сейчас мы рассмотрим ещё одно общее свойство определителя, важность которого для построения дальнейшей теории заставляет нас уделить ему особое внимание.

Предложение 3.16. Пусть , тогда

. (3.31)

◄ Из предложения 3.14 следует, что для матрицы найдется такая матрица , что матрица является верхнетреугольной и , а для матрицы найдется такая матрица , что матрица является верхнетреугольной и . Заметим, что при этом матрицы и являются произведениями элементарных матриц, порождаемых трансвекциями.

Поэтому

.

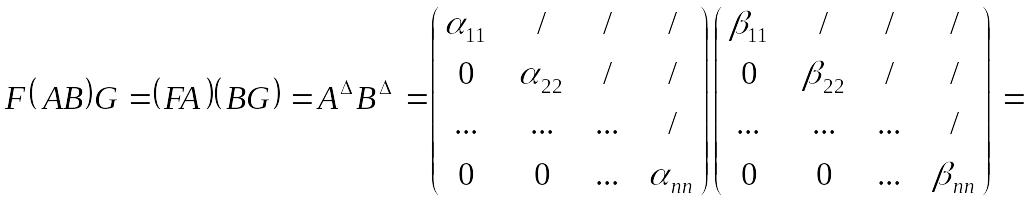
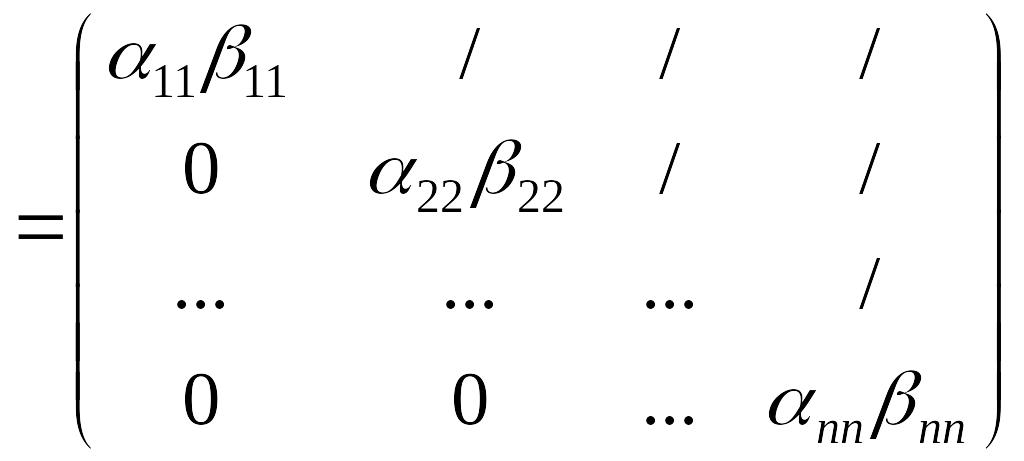На основании свойства 5 элементарных преобразований (см. Лекцию III, 1.10) матрицы и при умножении матрицы не меняют её определителя. Отсюда, учитывая предложение 3.13, получаем, что

. ►

10. Формула обратной матрицы

В качестве первого приложения рассмотренного выше свойства определителя мы получим новый критерий обратимости квадратной матрицы и, самое главное, формулу обратной матрицы для квадратной матрицы общего вида. Но вначале докажем одно вспомогательное утверждение.

Предложение 3.17. (Лемма о «трансплантации»). Пусть , а матрица получена из матрицы путем «трансплантации» произвольного вектора-строки вместо строки , . (Из матрицы вырезается строка , а на её место вставляется строка .) Тогда

, , (3.32)

где , – алгебраические дополнения элементов строки .

◄ Применим к матрице предложение 3.15, проводя разложение по строке ,

,

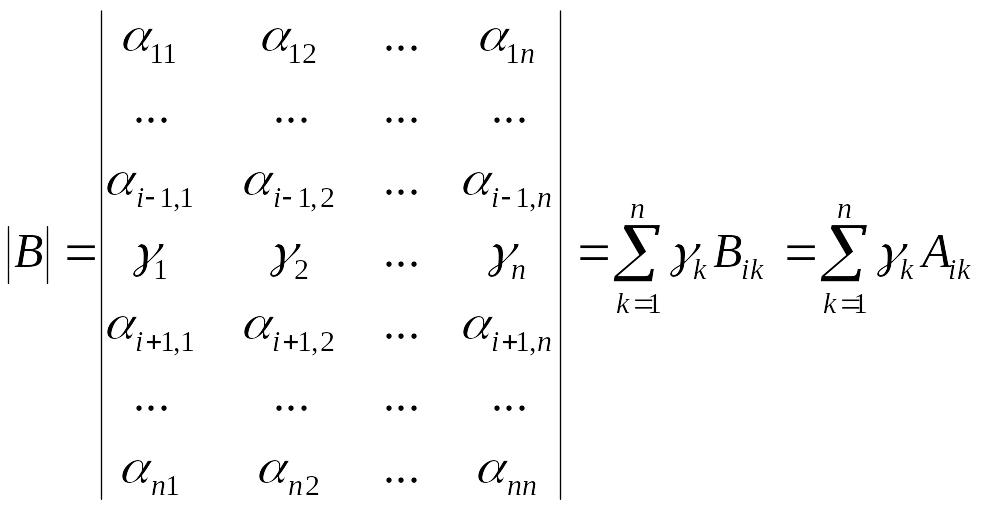так как , . Здесь мы пользуемся тем свойством, что алгебраические дополнения элементов какой-либо строки матрицы не зависят от самих элементов этой строки. ►

Предлагаем читателю самостоятельно сформулировать и доказать аналог леммы о «трансплантации» для случая столбцов.

Предложение 3.18. Пусть , тогда

(3.33)

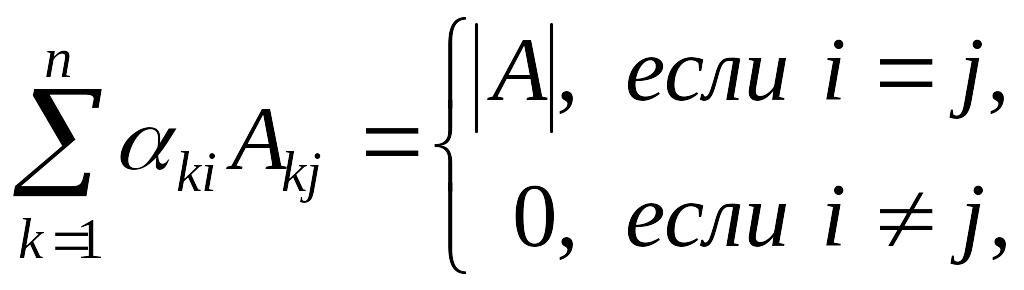(3.34)

◄ Докажем, например, формулу (3.33). Случай рассмотрен в предложении 3.15. Пусть . Тогда по лемме о «трансплантации» (см. (3.32))

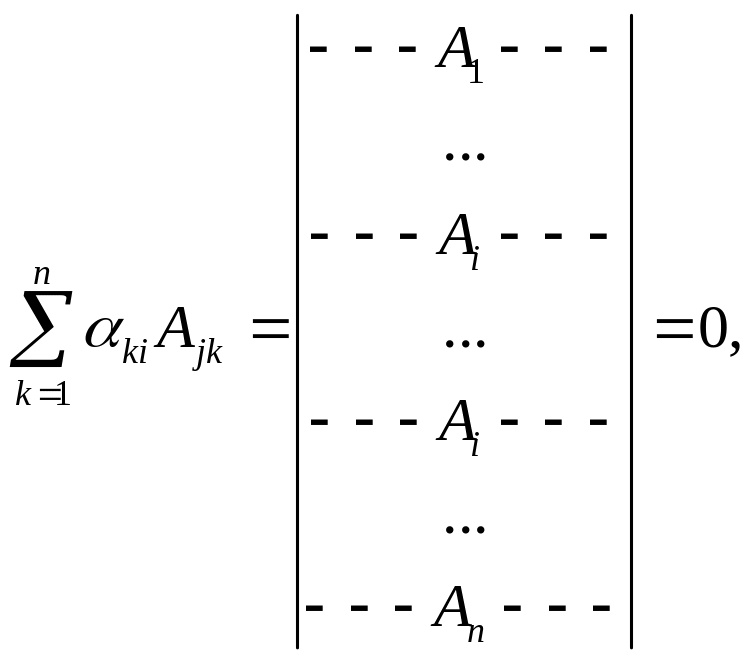
так как определитель имеет две одинаковые строки на i-ом и на j-ом местах. Формула (3.34) доказывается аналогичным образом. ►

Определение. Матрицу будем называть вырожденной, если . В противном случае матрица называется невырожденной.

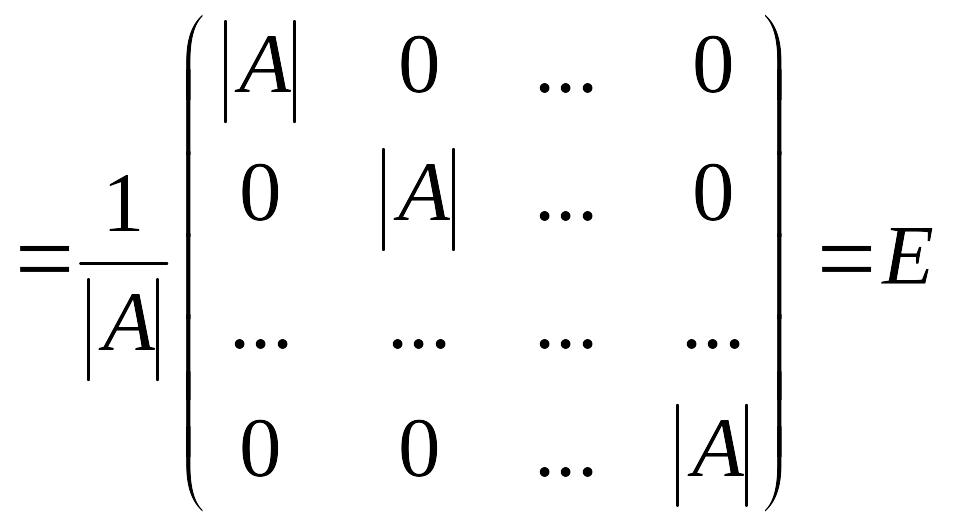
Предложение 3.19 (Критерий обратимости матрицы). Для того, чтобы матрица была обратимой, необходимо и достаточно, чтобы она была невырожденной.

Если матрица невырожденная, тогда

, (3.35)

где матрица

(3.36)

представляет собой транспонированную матрицу алгебраических дополнений элементов матрицы .

◄ Необходимость. Пусть . Тогда существует такая матрица , что . В силу предложения 3.16 . Следовательно .

Достаточность. Пусть . Тогда существует матрица 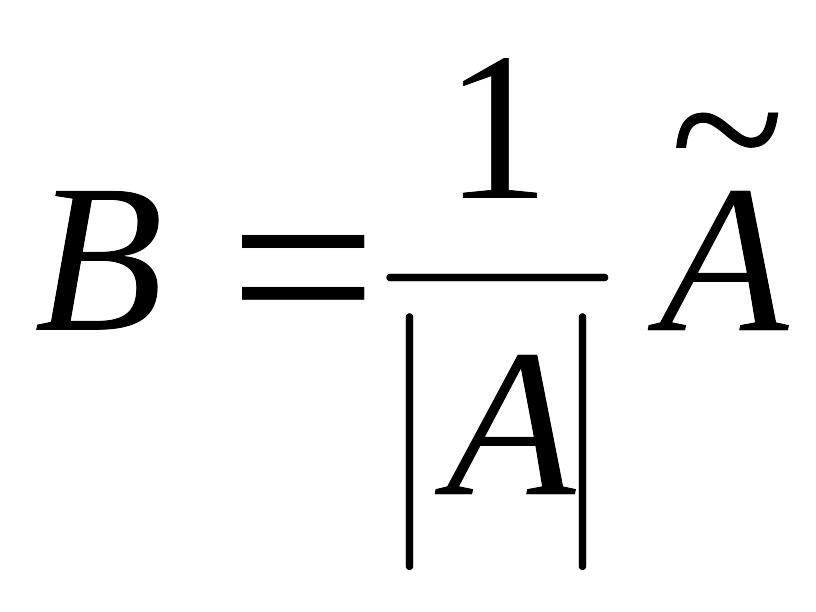. Для того, чтобы доказать, что , нужно проверить два равенства

и .

Проверим, например, первое равенство. Используя свойство 5) операции умножения матриц (см. Лекция I, 1.7) и формулу (3.33), получаем, что

.

Равенство предлагаем читателю проверить самостоятельно. ►

Пример 9. Пусть

и .

Тогда по формулам (3.35), (3.36)

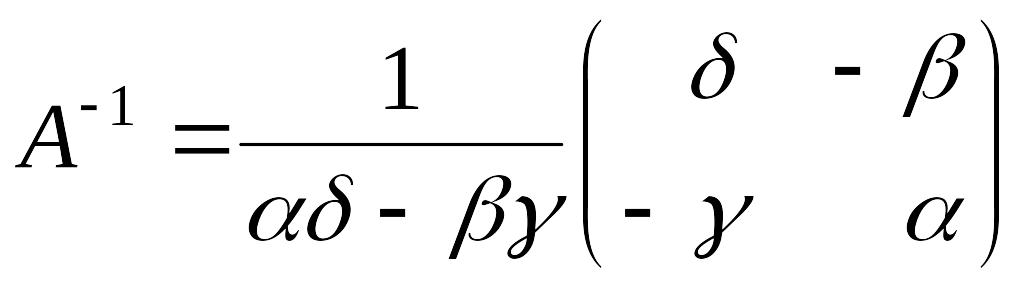. (3.37)

Эту формулу удобно применять на практике. Однако, для матриц более высокого порядка ( ) формулы (3.35), (3.36) с вычислительной точки зрения мало пригодны ввиду их громоздкости. И поэтому в этом случае следует использовать описанный в предыдущей главе алгоритм отыскания обратной матрицы методом Гаусса.