19. Алгоритм Брезенхема растровой развертки отрезков прямых.

Существует два вида реализации этого алгоритма: вещественный и целочисленный. Вещественный служит базой для построения целочисленного алгоритма. Работа вещественного алгоритма базируется на расчете дополнительной переменной – оценки отложения точки аппроксимации от истинного направления (обозначим эту оценку как е).

Р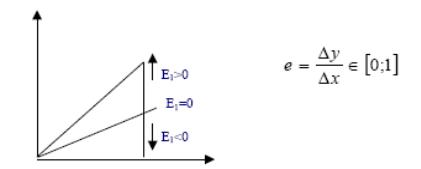 ассмотрим работу алгоритма в I квадранте:

Для удобства работы величину е изменяют таким образом, чтобы она в крайних точках имела значения с противоположенными значениями:

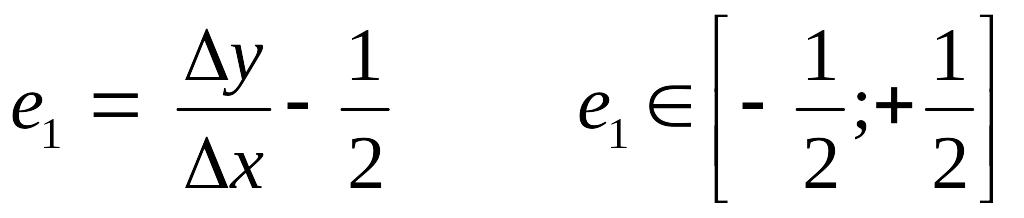
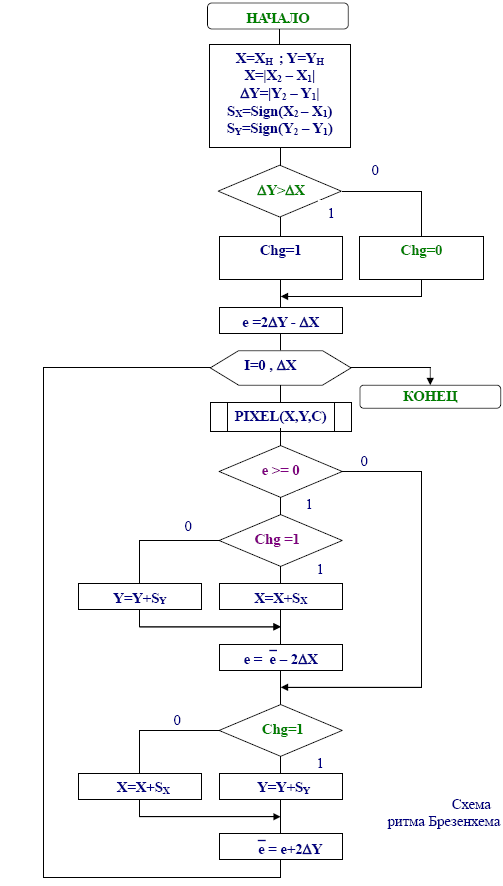
Недостатки:

1) наличие операций деления.

2) вещественный характер вычислений.

Для того, чтобы работать в одной области определения с растровыми данными, осуществляется переход к целочисленным значениям оценки е:

Алгоритм основанный на данном вычисление оценки, позволяет эффективно реализовать растровые разложения отрезка как на аппаратном, так и на программном уровнях.

Растровая развертка окружностей

Построения окружностей и эллипсов можно осуществлять двумя способами:

1) используя уравнения тригонометрии и аналитической геометрии;

2) с использованием численных методов.

Построение окружности с использованием аналитических выражений. В простейшем случае отображение окружности в растр можно осуществить при помощи аналитической зависимости между координатами X и Y. Алгоритм будет иметь вид:

Данный алгоритм легко модернизировать для случая построения эллипса. Необходимо заменить радиус R в уравнениях для вычисления координат на полуоси R_x и R_y. Аналогичным образом можно учесть другое соотношение координат окружности вида:

x² + y² = R²

Отсюда можно вычислить соответствующее значение у:

И в том и в другом случае алгоритм растровой развертки окружности достаточно прост для программирования, однако, его вычислительная сложность слишком велика для реализации в составе ядра базовой графической системы. Это объясняется наличием тригонометрических функций в первом случае и степенных – во втором. Поэтому использовать подобные процедуры или функции в составе базовой графической системы не целесообразно. Необходимо разработать такие алгоритмы, которые бы максимально эффективно выполняли растровую развертку окружности при минимальной вычислительной сложности. Один из них приведен ниже.

Конец 19 вопроса.

20. Алгоритмы Брезенхема растровой развертки окружностей.

Брезенхемом был предложен алгоритм аппроксимации разложения окружности в растр, использующий целочисленную арифметику. Кроме отказа от длинных операций и сложности арифметических вычислений трудоемкость этого алгоритма можно сократить в 8 раз, если учесть симметричный характер окружности. Рассмотрим окружность, центр которой расположен в начале координат. При элементарных изменениях можно получить алгоритм, отображающий окружность в произвольном положении. Окружность имеет бесконечное множество осей симметрии, однако, для практики важно наличие восьмисторонней симметрии. Достаточно вычислить величины координат одной точки (х, у), после чего без дополнительных вычислений можно вывести на экран еще 7 точек (см. рис.4.6).

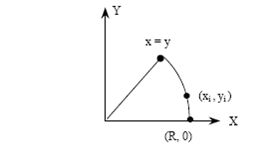
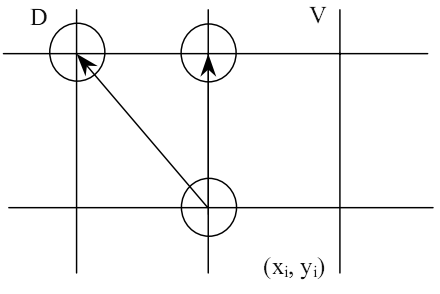
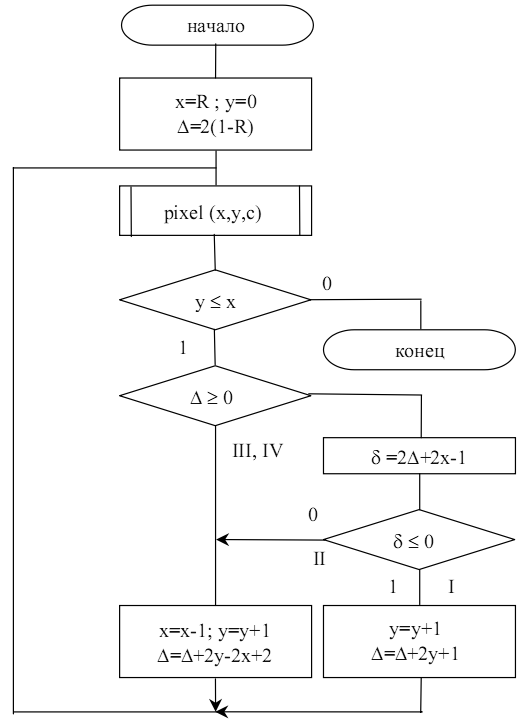
Рассмотрим реализацию алгоритма Брезенхема в первом октанте, так как на основании точек первого октанта можно восстановить всю окружность. В качестве начальной точки изображения выберем точку с координатами (R,0), где R – радиус разлагаемой в растр окружности (см. рис.4.7).

Для любой точки с произвольными координатами (xi , yi), находящейся на окружности при построении в выбранном направлении возможны два варианта перехода от текущего аппроксимирующего пиксела к следующему (см. рис.4.8).

При этом координаты очередного аппроксимирующего пикселя составят следующие значения:

(xi , yi) → (xi , yi + 1) - в вертикальном направлении;

(xi , yi) → (xi - 1 , yi + 1) - в диагональном направлении.

Аппроксимирующий пиксель необязательно будет попадать на окружность радиуса R. Он может находиться либо ближе, либо дальше от центра окружности, т. е. радиус аппроксимирующей окружности может отличаться от радиуса исходной окружности. При этом отличие может изменяться от шага к шагу.

Выберем в качестве меры отклонения радиусы между квадратами радиусов исходной и аппроксимирующей окружностей.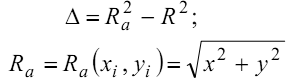

Таким образом, зная координаты точки аппроксимации, можно определить конкретное отклонение окружности на каком-либо i-том шаге:

Для того, чтобы выбрать направление перехода (либо в вертикальном, либо в горизонтальном направлении), необходимо оценить отклонения от исходного радиуса в этих двух случаях и сравнить их между собой.

При переходе в вертикальном направлении на следующем шаге получим

При переходе в диагональном направлении:

В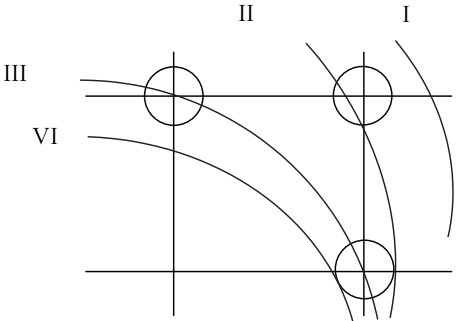 ычисления по формулам (4.2) – (4.4) содержат квадраты чисел поэтому желательно упростить эти выражения. Этого можно добиться если рассмотреть конкретные возможные варианты пересечения линий окружности с сеткой растра. В первом октанте возможны следующие четыре вида пересечений линий окружности и сетки растра (рис. 4.9).

В случаях I и II получается, что Ra< R, т.е. аппроксимирующие точки лежат внутри аппроксимирующей окружности. В третьем случае Ra=R (точка аппроксимации лежит на окружности). В IV случае Ra>R, т.е. все аппроксимирующие точки находятся дальше от центра. Таким образом, для случаев I и II можно выбрать

Следовательно, определить величину ∆ можно, осуществив выбор очередной точки аппроксимации. Остается разделить варианты I и II. Рассмотрим каждый из этих случаев отдельно.

Вариант I

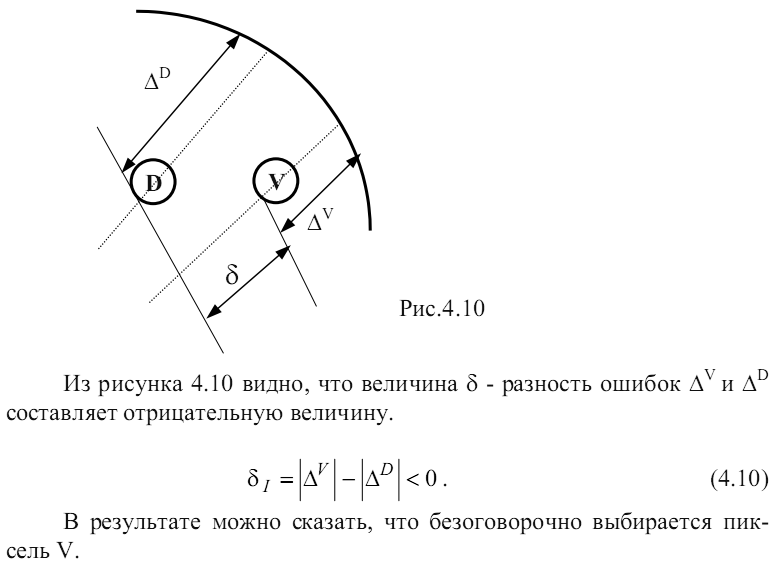
Вариант II

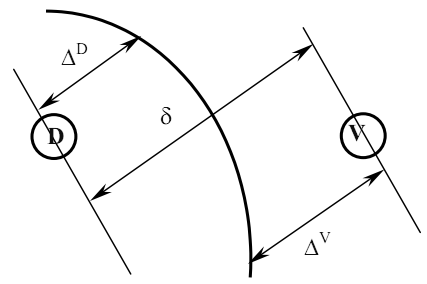
Возможен выбор между точками V и D (рис.4.11).

Конец 20 вопроса.