2. Корреляционное отношениеη (эта). Оно измеряет степень корреляции при любой ее форме.

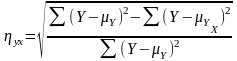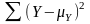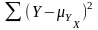где: – сумма квадратов отклонений индивид-ых знач-ий Y от общей сред. арифметич. μ_Y; – сумма квадратов отклонений вариант от групповых средних 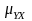, соответств-их опред-ым, фиксир-ым знач-ям независ-ой переменной X.

Д/вычисления корреляц-го отнош-я знач-я независ-го признака X располагают по ранжиру в возрастающем порядке и разбив. весь ряд наблюдений на 4–7 групп с таким расчетом, чтобы в каждой группе по ряду X было не <ее 2ух наблюдений  опред-ют общую среднюю μ_Y, групповые средние , соответствующие каждой фиксир-ной группе X, и суммы квадратов отклонений д/общего и группового варьирования признака Y.

При >ом объеме наблюдений (n> 30) опред-ся сумма квадратов отклонений группового варьирования , сумма квадратов отклонений общего варьирования и вычисляется корреляц-ое отнош-е по ф-ле:

Сумма квадратов отклонений групповых средних от общей средней μ_Y (групповое варьирование) хар-зует ту часть варьирования признака Y, кот. связ. с изменчивостью признака X. Сумма квадратов разностей м/у каждой величиной и общей средней μ_Y, т. е. , хар-зует общее варьирование признака Y.

Билет11

1. Взвешенная средняя арифметическая. Иногда знач-я признака должны входить в сумму с неодинаковой поправкой. Эта поправка, выраженная опред-ным множителем, наз. матем-ким весом значения. Средняя, рассчитанная д/значений признака с неодинак-ми весами, наз. взвешенной средней и рассчит-ся по формуле: 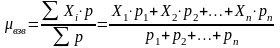, где X_i — значение признака, варианта; p — математический вес усредняемого значения.

Чтобы рассчитать взвешенную средн. арифметич., необх. каждое знач-е признака помножить на его вес, все эти произвед-я сложить и полученную сумму разделить на сумму весов.

Н: рез-ты 2ух исслед-ий длины хоботка пчел: в 1ом случае средняя длина хоботка 6,6 мм, в 2ом – 6,0 мм. Получить общую среднюю, причем известно, что в 1ом исслед-ии были измерены хоботки у 100 пчел, во 2ом – у 20.

Знач-ми признака явл. средние μ₁ = 6,6 и μ₂ = 6,0 мм; их весами – численности групп n₁ = 100 и n₂ = 20. Взвешенная средн. арифметич.:

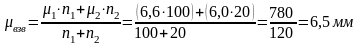
2. Уравнение прямолинейной регрессии.

Коэффициент прямолинейной регрессии показ., на сколько от своей средней отклоняется 2ой признак, если 1вый признак от своей средней отклон-ся на ед-цу измерения: (X₂-μ₂)=R_2/1 (X₁- μ ₁) Обозначая X₁ ч/з х, X₂ ч/з у, R_1/2 ч/з b и произведя преобразования этого выражения, получаем рабочую ф-лу прямолинейной регрессии: y=a+bx По этой ф-ле, зная знач-е х (аргумент), можно опред-ть знач-е у (ф-ция) без непосредственного его измерения: необх. аргумент х помножить на коэф-т регрессии и к полученному произвед-ию прибавить (или отнять) свободный член а.

На основе уравнения прямолинейной регрессии можно заранее рассчитать значение ф-ции д/каждого значения аргумента.

Билет 12

1. Средняя геометрическая. Чтобы получить среднюю геометрич-ю д/группы с n данными, нужно все вар-ты перемножить и из полученного произвед-я извлечь корень n-й степени:

где G – средняя геометрич-я, n – число значений, ΠX_n – произвед-е вар-тов.

Если число значений > 2х, то извлечение корня n-й степени затруднeно, поэт. обычно знач-е средней геометрич-ой находят путем логарифмир-я величин, входящих в основную ф-у:

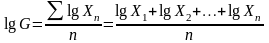.Для проверки правильности вычисления средней геометрической можно исп-вать принцип единства суммарного действия. Произведение всех знач-ий X_n = произведению n выравненных знач-ий, = средней геометрич..

Применяется средняя геометрич-я во всех случаях, когда необх-мо узнать или планировать средние приросты за опред-ый период. При расчетах среднего попериодного прироста возможны 2 способа примен-я средней геометрич-ой:

1)применяется, когда им-ся сведения о приростах за каждый период, выраженных в % или долях от начала каждого периода:

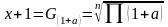где: х – средний попериодный прирост за ряд периодов равной продолжит-ти; а – фактич-ий прирост за тот или иной период, выраженный в долях; n – число периодов; Π(1+а) – произвед-е величин (1+а).

Д/нахождения среднего прироста по 1му способу нужно долю фактич-го прироста за каждый период +1, полученные величины (1+а) перемножить, из их произвед-я извлечь корень n-й степени и -1.

2)если периодов много (n > 2), то извлеч-е корня надо проводить логарифмир-ем:

По этой ф-ле находят логарифмы средней геометрич. из величин (1+a)  находится сама величина G_(1+a) и -1 получается искомая средняя доля прироста.

2. Коэффициент прямолинейной регрессии. Прямолинейная корреляция отличается тем, что при этой форме связи каждому из одинаковых изменений 1го признака соответствует вполне опред-ное и тоже одинаковое в среднем изменение др. признака, связ-го с 1вым или зависящего от него. Та величина, на кот. в среднем изменяется 2ой признак, при измен-ии 1го на ед-цу измерения, наз. коэффициентом регрессии:

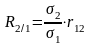где R_1/2 — коэф-т регрессии 2го признака по 1му; _ — среднее квадратич-ое отклонение 2го признака, кот. измен-ся в связи с измен-ем 1го; ₁ — среднее квадратич-ое отклонение 1го признака, в связи с измен-ем котю измен-ся 2ой признак; r₁₂ — коэф-т корреляции м/у 1ым и 2ым признаками.

Ошибка коэф-та регрессии = ошибке коэф-та корреляции, умноженной на отношение сигм: .

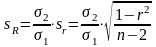Критерий достоверности коэф-та регрессии = критерию достоверности коэф-та корреляции:

,

Билет 13

1. Средняя квадратическая вычисляется по ф-ле: 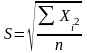, Она = корню квадратному из суммы квадратов данных, деленной на их число. Употребляется средняя квадратич-я при расчете средних радиусов окружностей.

Н: измерения диаметров колоний, полученных от посева микробов опред-го вида (в мм): 15; 20; 10; 25; 30. Д/сравнения этого посева с др. необх. определить средний диаметр колоний. По ф-ле средней квадратич.:

.

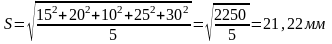Средняя арифметичю диаметров:

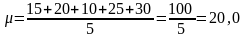дает неправильную хар-ку группы.

2. Достоверность разности двух коэффициентов корреляции. Достоверность разности коэф-тов корреляции опред-ся по ф-ле: где t_d —критерий достоверности разности коэф-тов корреляции; d=r₁-r₂—разность коэф-тов корреляции; —ошибка разности, равная корню квадратному из суммы квадратов ошибок обоих сравниваемых коэф-тов корреляции; t_st — стандартн. знач-я критерия Стьюдента; v — число степеней свободы д/разности коэф-тов корреляции, = сумме чисел степеней свободы обоих коэф-тов: v= n₁–2 + n₂–2=n₁+ n₂–4.

Билет 14.

1.Средняя гармоническая рассчитывается по ф-ле:

где X_i — значение признака, варианта; n — число значений

Применяется средняя гармоническая при усреднении меняющихся скоростей.

H: почтовые голуби к месту кормежки летят со скор-ю 50 км/час, а обратно – со скор-ю 40 км/час. Выяснить среднюю скорость полета для обоих направлений (расстояния, очевидно равны), сделать это можно, рассчитав простую среднюю гармонич-ю д/2х знач-ий 50 и 40:

.

2.Доверительные границы коэффициента корреляции Доверительные границы генерального знач-я коэф-та корреляции нах-ся по ф-ле: , где и — генеральное и выборочное знач-я коэф-та корреляции;  = t s_r — возможная погрешность при определении генерального парам-ра; t_st— критерий Стьюдента при числе степеней свободы  = n – 2; s_r — ошибка коэф-та корреляции.

Билет 15.

1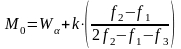 . Мода такая варианта или класс распред-я вариант, кот. в исследуемой группе встречается наи>ее часто. В кач-ве 1го приближения можно принять за моду средину модального класса.

1. Значение моды можно получить по ф-ле, где М₀ — мода; W_α — начало модального класса; k — величина классового промежутка; f₁ — частота класса, предшествующего модальному; f₂ — частота модального класса; f₃ — частота класса, следующего за модальным.