§ 2. Окремі класи диференціальних рівнянь, що інтегруються в квадратурах або допускають зниження порядку

Диференціальні рівняння порядку п інтегруються в квадратурах дуже рідко. У цьому параграфі ми розглянемо ті класи (типи) диферен­ціальних рівнянь вищих порядків, які можуть бути проінтегровані в квадратурах або порядок яких можна знизити.

Д иференціальне рівняння виду

(20)

д е функція / (х) неперервна на відрізку [а; b], інтегрується в квадра­турах. Справді, запишемо його у вигляді

а бо

Т оді (21)

де С₁ — стала інтегрування.

Отже, диференціальне рівняння (20) порядку п ми звели до ди­ференціального рівняння (21) порядку п — 1.

Рівняння (21) запишемо у вигляді

звідки після інтегрування знаходимо

(22)

де С₂ — стала інтегрування.

Я кщо п > 2, то від диференціального рівняння (22) (п — 2)-го порядку переходимо до диференціального рівняння

де С₃ — стала інтегрування, і т. д. Через п кроків дістанемо функцію

яка є загальним розв'язком диференціального рівняння (20).

ПРИКЛАДИ

1. Знайти загальний розв'язок диференціального рівняння

Р о з в ’ я з а н н я. Послідовно дістаємо:

Отже остаточно маємо

Тепер розглянемо деякі типи диференціальних рівнянь, які до­пускають зниження порядку.

1 . Нехай маємо диференціальне рівняння

(26) яке не містить шуканої функції у та її перших k — 1 похідних, . Введемо нову невідому функцію

Д иференціальне рівняння (26) п-го порядку переходить у дифе­ренціальне рівняння (n-k)-го порядку

(27) Отже, порядок диференціального рівняння знизився на k одиниць. Припустимо, що рівняння (27) проінтегрували, тобто знайшли його загальний розв'язок

(28)

де С₁ С₂, ..., с„_а: — довільні сталі.

Загальний розв'язок (28) називають проміжним інтег­ралом диференціального рівняння (26).

З наючи проміжний інтеграл, можна знайти загальний розв'язок рівняння (27). Підставляючи в рівність (28) значення діста­немо диференціальне рівняння

Це рівняння є рівняння типу (20). Отже, воно інтегрується в квад­ратурах, його загальний розв'язок має вигляд

ПРИКЛАД

Знайти загальний розв'язок диференціального рівняння

Розв'язання. Застосовуємо підстановку

z = У'.

Тоді рівняння набирає вигляду

2хг' = z.

Дістали рівняння першого порядку, яке допускає відокремлення змінних

Звідси знаходимо

а бо

де — стала Інтегрування.

Підставивши в останню рівність значення z=y’, матимемо диференціальне рівняння першого порядку

Загальний розв'язок цього, а отже, і заданого рівняння є

2. Нехай маємо диференціальне рівняння

(29)

яке розв’язне відносно у^(п):

(30)

Застосуємо підстановку

Т оді рівняння (30) перетворюється у диференціальне рівняння першого порядку відносно функції z:

я ке при допускає відокремлення змінних

З відси

Нехай

П ідставивши сюди значення матимемо диференціальне рівняння

типу (20).

ПРИКЛАД

Знайти загальний розв'язок диференціального рівняння

(при а = 0 це диференціальне рівняння типу (20)).

Розв'язання. Задане рівняння є типу (29). Ввівши підстановку

м атимемо

Відокремивши змінні, дістанемо

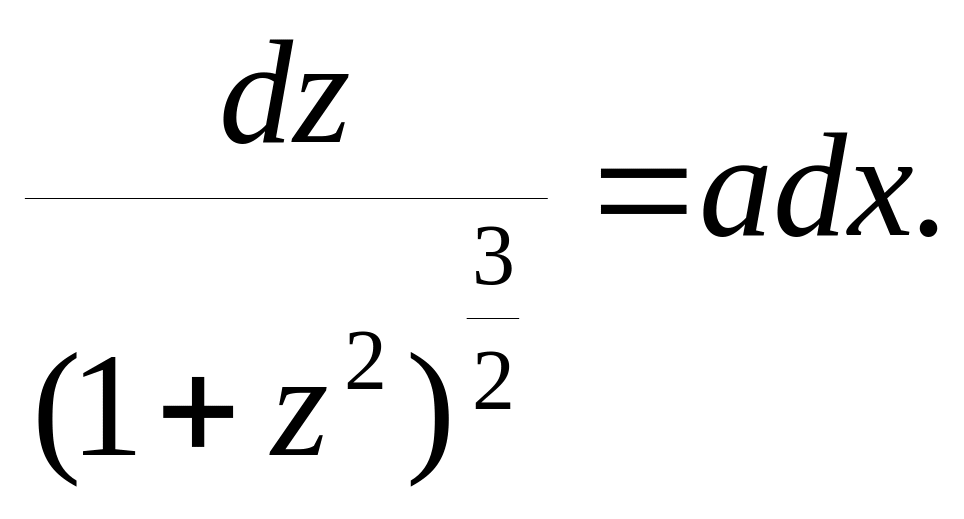
З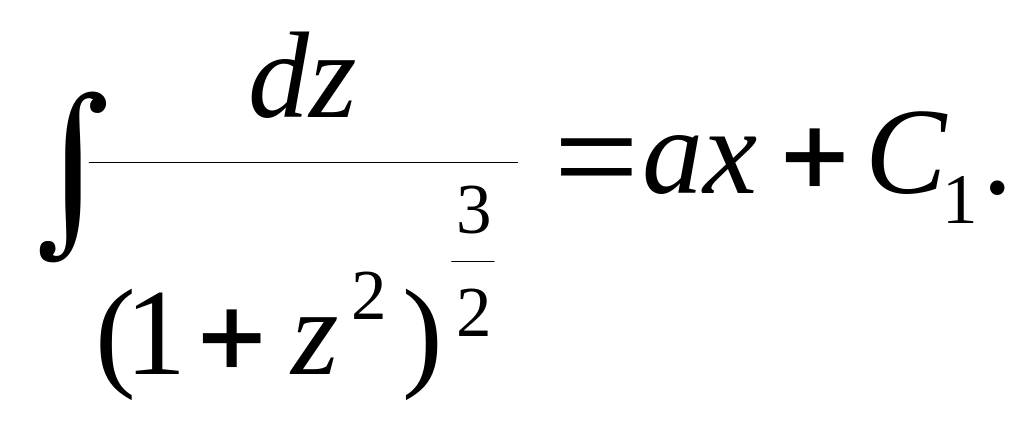 відси

І нтеграл у лівій частині є інтеграл від біномного диференціала. Тут

Використовуємо третю підстановку

Тоді інтеграл набирає вигляду

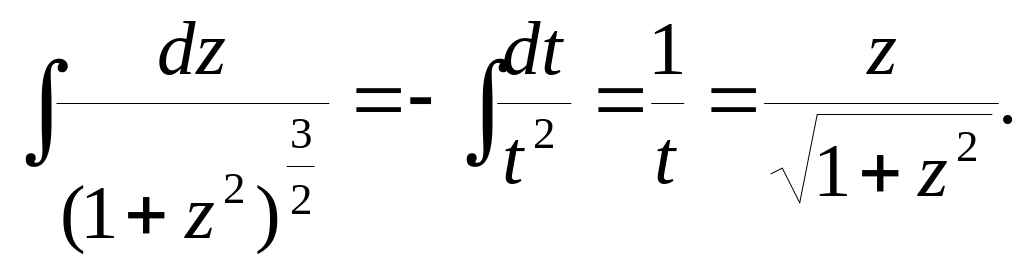
Отже,

З відки

( тут взяли тільки одне значення для z).

Підставимо значення z= у'. Матимемо

І нтегруючи це рівняння, знаходимо загальний розв'язок заданого диференціального рівняння:

З. Розглянемо диференціальне рівняння виду

яке можна розв'язати відносно старшої похідної

Застосовуємо підстановку

Т оді рівняння (32) набирає вигляду

(33)

П омноживши обидві частини цього рівняння на , матимемо

Звідси

або

д е С₂ — стала інтегрування. Нехай

Підставивши сюди значення дістанемо диференціаль­не рівняння (п — 2)-го порядку

типу (20).

4. Розглянемо, нарешті, диференціальне рівняння

(34)

яке не містить незалежної змінної х. Це рівняння допускає зниження порядку на одиницю.

С правді, введемо підстановку

Т оді

Отже, похідна другого порядку виражається через нову невідому

функцію z і її похідну першого порядку . Знайдемо

і т. д.

За методом індукції можна довести, що порядок усіх наступних похідних також знижується на одиницю.

Таким чином, від диференціального рівняння (34) n-го порядку перейдемо до диференціального рівняння

(п — 1)-го порядку.

ПРИКЛАД

З найти загальний розв'язок диференціального рівняння

Розв'язання. Застосовуємо підстановку у' =z. Тоді задане рівняння за­пишемо так:

Це рівняння першого порядку, і воно допускає відокремлення змінних:

З відси

або

Підставивши сюди значення z, матимемо

або

Про інтегрувавши обидві частини, знайдемо

а бо

де С₁ і С₂ — сталі інтегрування.

28