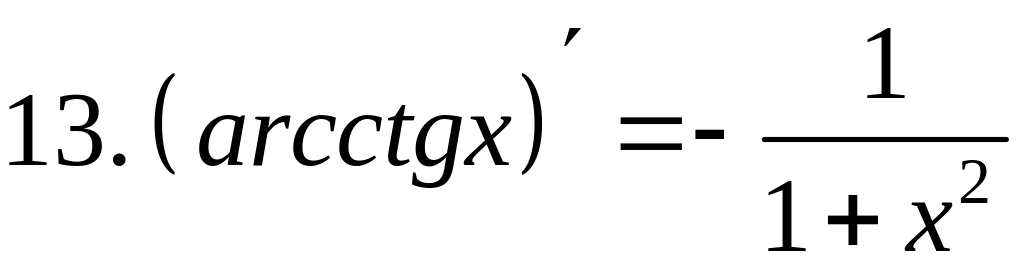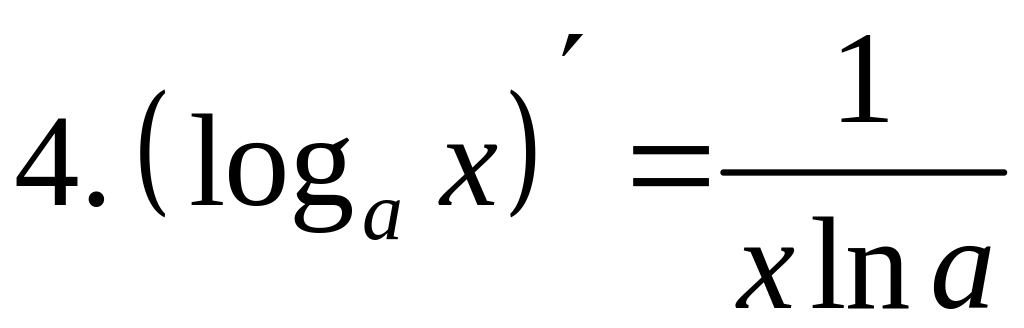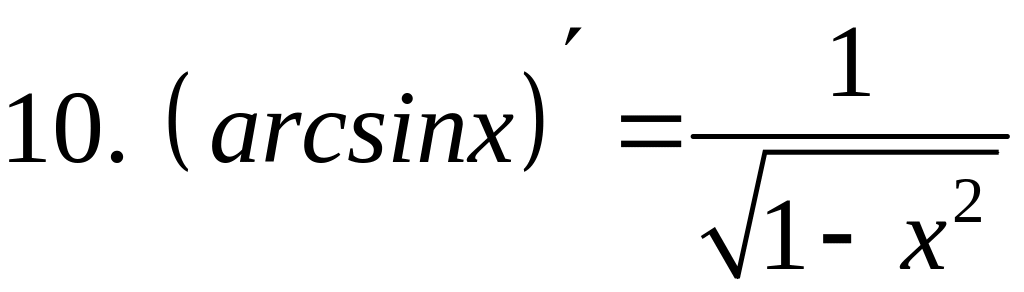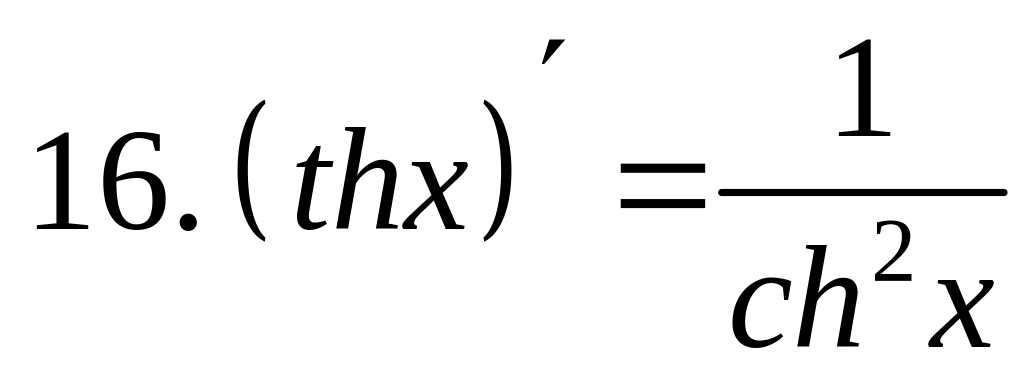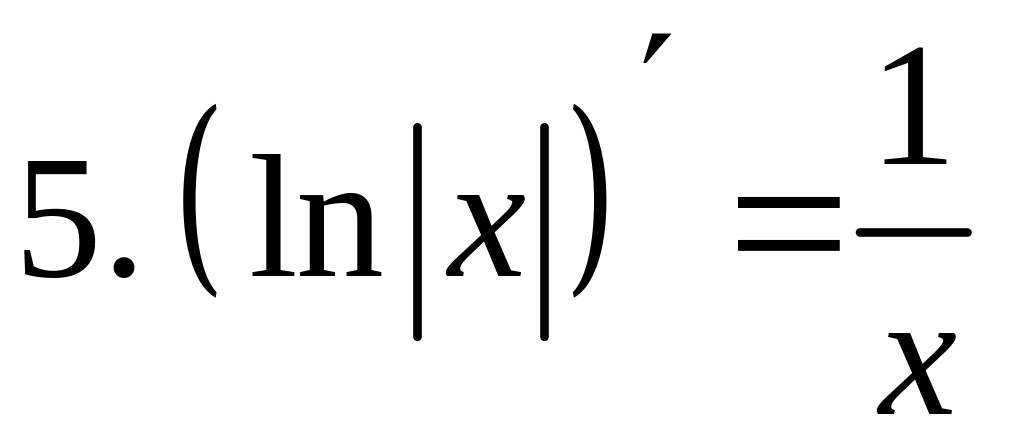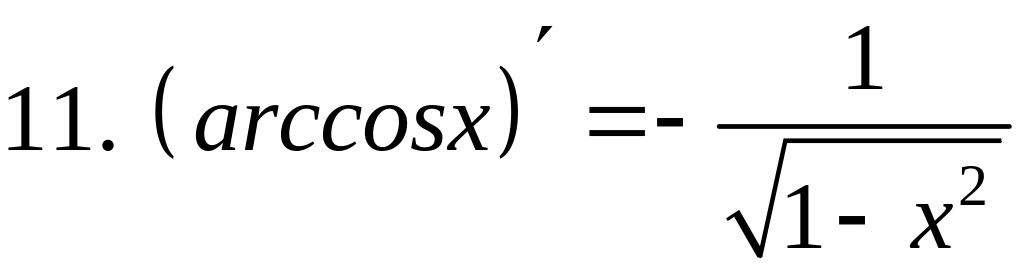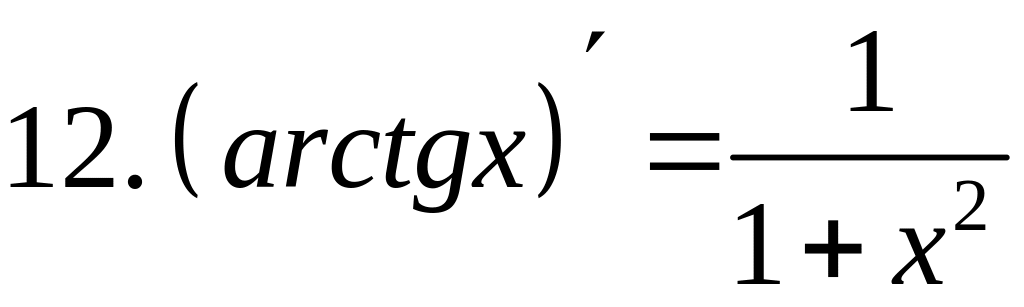§5. Производная обратной и сложной функций. Таблица производных

Теорема 1. Пусть функция определена, непрерывна и строго монотонна в окрестности точки и пусть ее производная в точке существует и отлична от нуля, Тогда обратная функция также имеет производную в точке , причем

. (1)

Доказательство. Существование обратной функции , непрерывной и строго монотонной в окрестности точки гарантирует теорема 3 §11 главы 4. Поэтому условия

и

эквивалентны и так как обе функции строго монотонны, то и . Запишем тождество

.

Переходя к пределу, имеем

Так как предел правой части существует, то существует и предел левой части, то есть

Теорема доказана.

Равенство (1) можно записать в симметричной форме

.

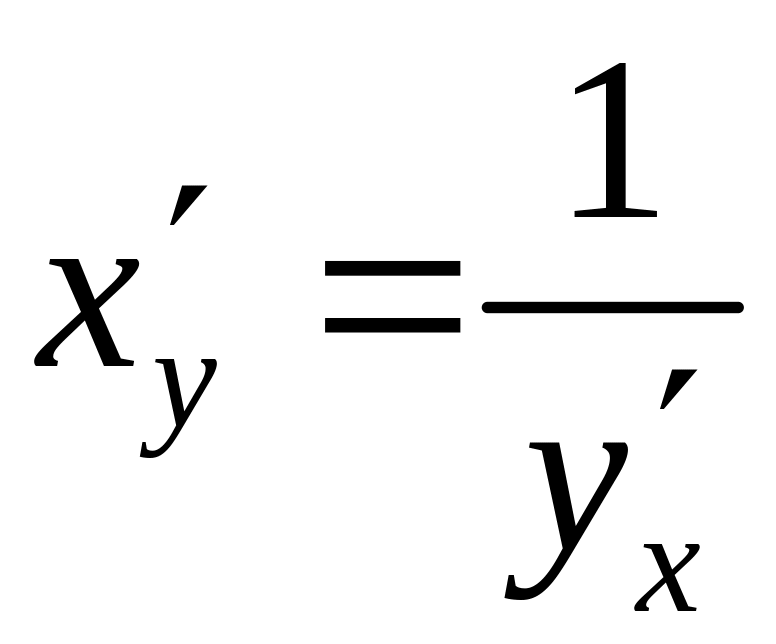Индекс показывает, по какой переменной берется производная.

Пример 1. Найти

Решение. .

Согласно имеем

.

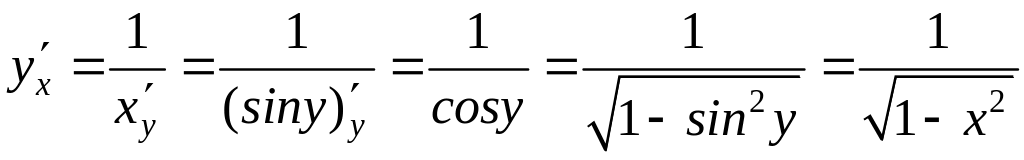Итак,

.

Пример 2.

.

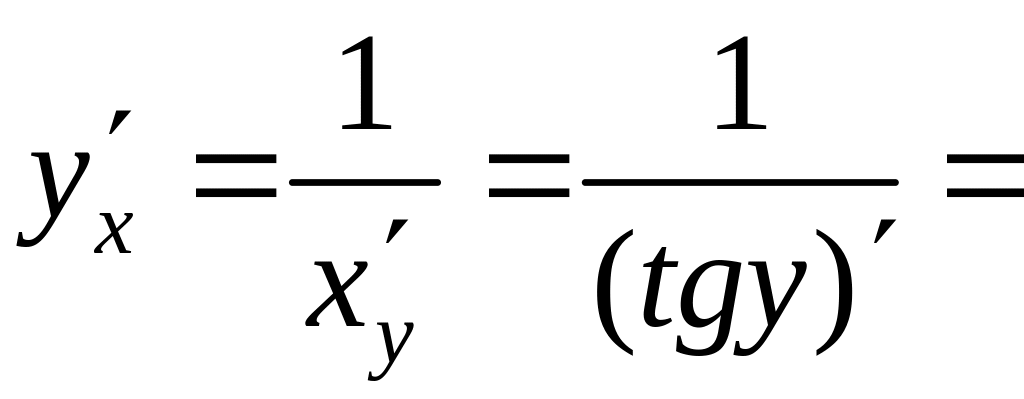
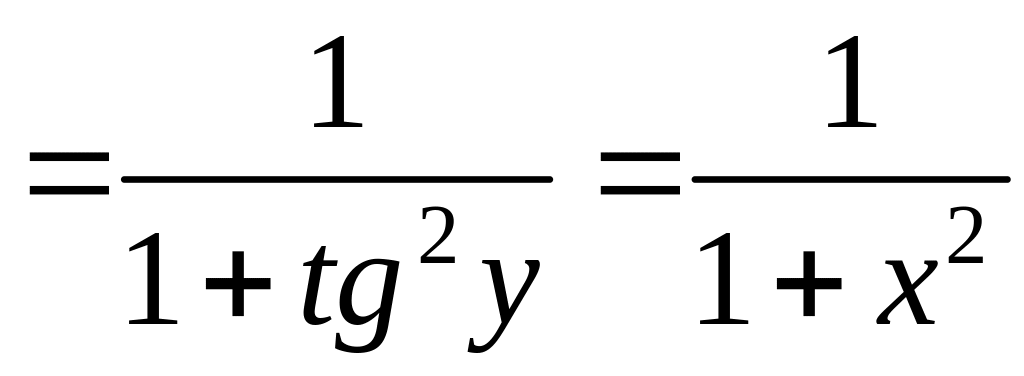Итак,

.

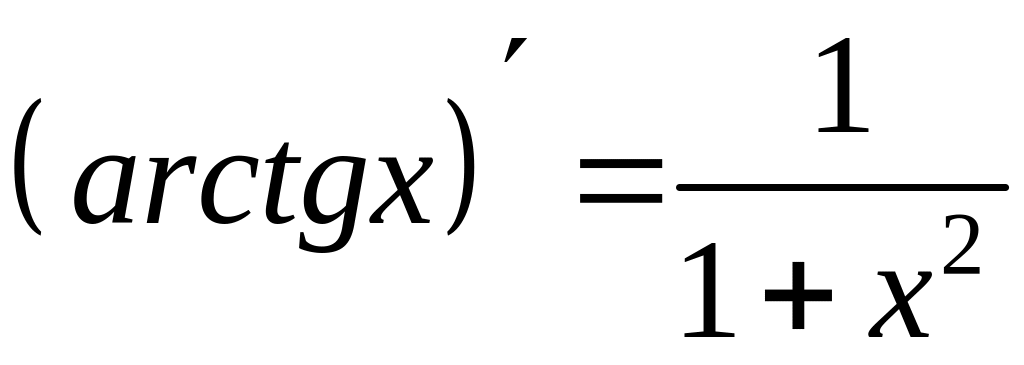Упражнение. Доказать, что    , .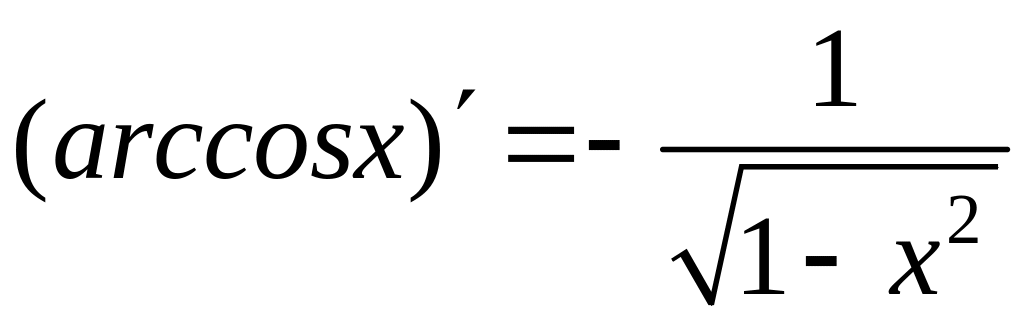

Если , а , то суперпозицию этих функций называют сложной функцией .

Теорема 2. Если и существуют, где , то существует и производная сложной функции в точке , причем

.

Доказательство. Так как функции и имеют производные в точках и соответственно, то и непрерывны в этих точках (см. §7). Сложная функция непрерывна в точке (см. теорему 2 §8 гл. 4), поэтому при . Функция дифференцируема в точке , поэтому

(см. §3). 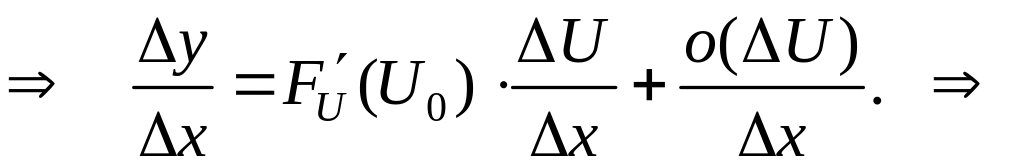 . Итак,

.

Теорема доказана.

Пример 3. Найти производную степенной функции .

Решение. , – сложная функция. Воспользуемся .

.

Итак,

Пример 4.     сложная функция.

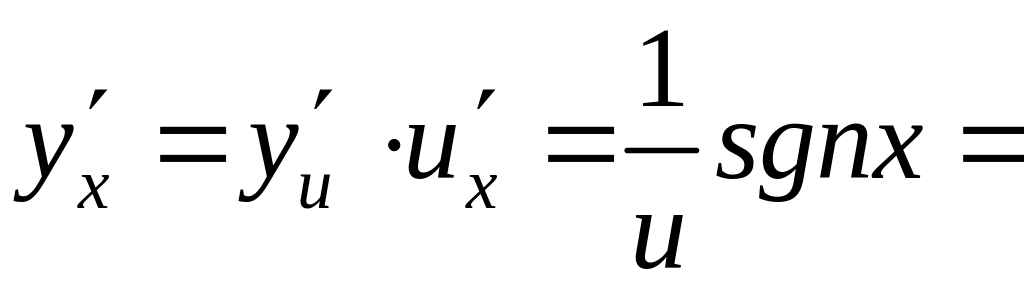
Итак,

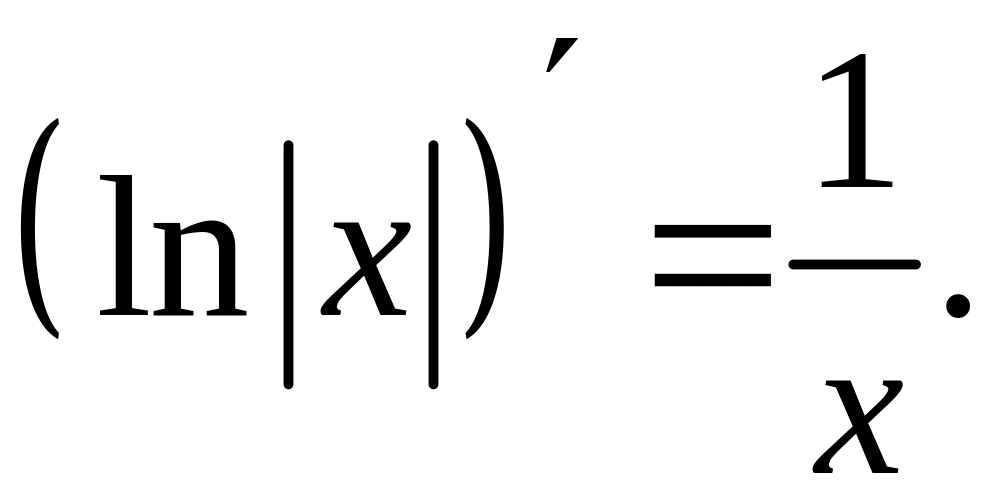
Пример 5.     сложная функция.

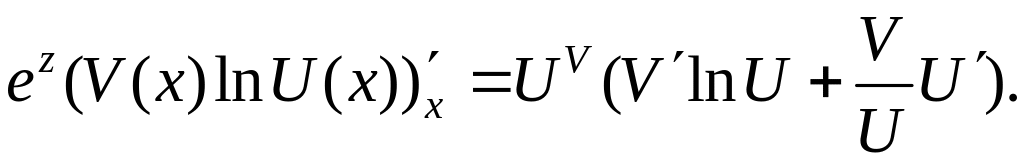
Замечание 1. Теорема 2 верна и для большего числа суперпозиций функций.

Пример 5. 

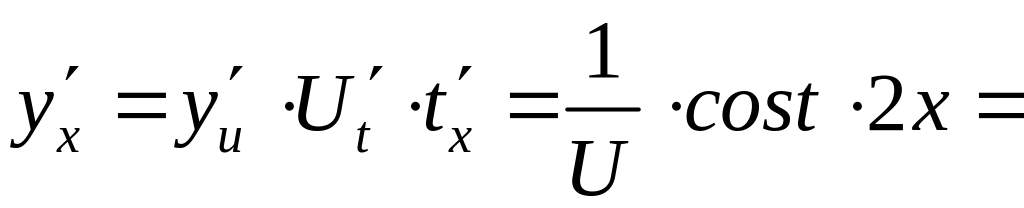
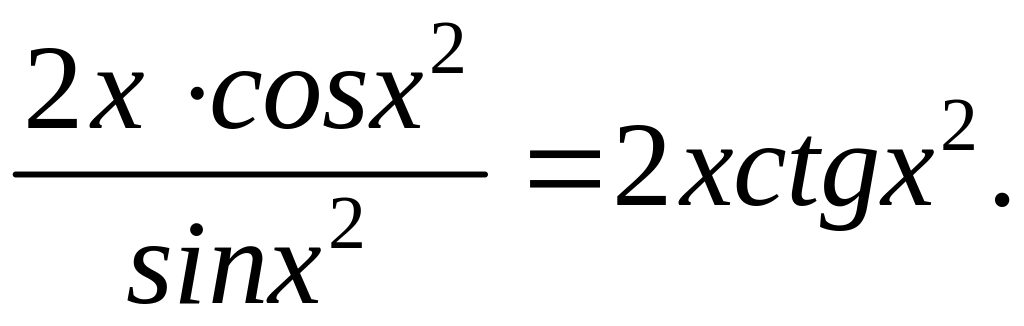
Сведем все вычисленные выше производные в таблицу (таблицу выучить наизусть).

Таблица

Замечание 2. Как видно из приведенных примеров, основные элементарные функции дифференцируемые. Из правил дифференцирования суммы, произведения, отношения, сложных функций следует, что любая элементарная функция имеет производную в области определения и является элементарной функцией в области определения.

§6. Производная высшего порядка. Формула Лейбница

Пусть функция определена на интервале и в каждой точке этого интервала имеет производную . Так как производная является функцией, определённой на интервале , то сама может иметь производную. Производная от производной называется второй производной, или производной второго порядка. Обозначают её так:

Аналогично можно ввести третью и так далее производную. n-я производная – это производная от -й производной

.

Функция называется n-раз непрерывно дифференцируемой в точке x, если существует некоторая окрестность этой точки, в которой

-я производная непрерывна. Естественно, что -я производная в этой точке – функция дифференцируемая.

Пример 1. .

Очевидно

(1)

Формулу можно доказать методом математической индукции.

В частности, если натуральное, то !, а при .

Пример 2. ,

(2)

Пример 3. ,

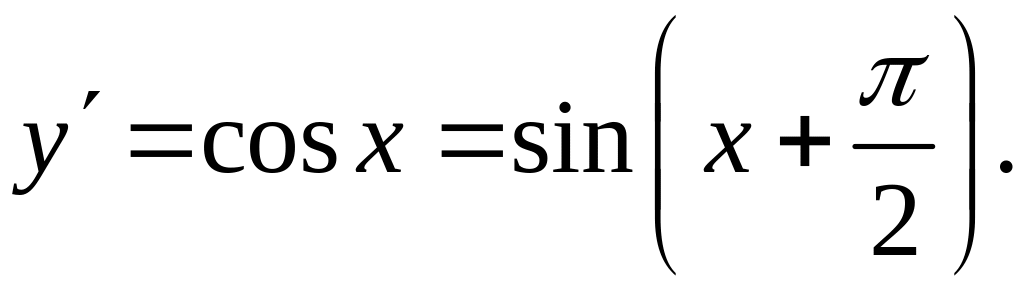
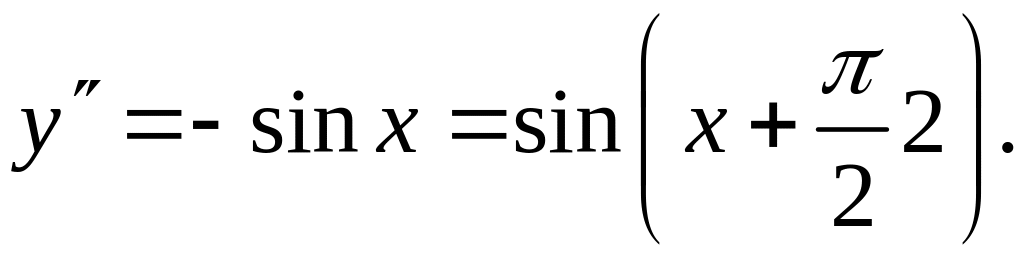
 – гипотеза.

.

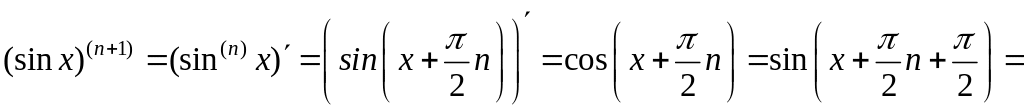
Формула доказана методом математической индукции.

Упражнения. Доказать, что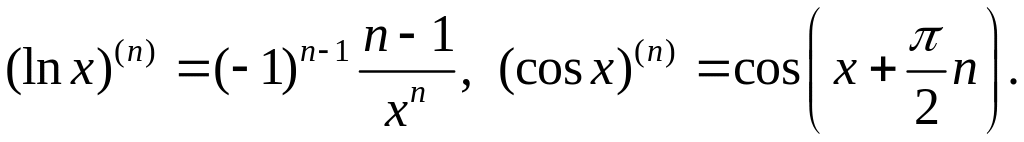

Очевидно, константу можно вынести за знак производной любого порядка, то есть

.

Производная от суммы двух функций равна сумме производных, то есть

,

если последние существуют.

Найдём теперь -ю производную от произведения двух функций. Докажем, что

, (3)

где Формула (3) называется формулой Лейбница.

Доказательство. Воспользуемся методом математической индукции, предварительно отметив, что

Проверим формулу (3) при .

– формула справедлива. Пусть (3) справедлива. Найдём -ю производную.

(введём обозначение в первой сумме)

.

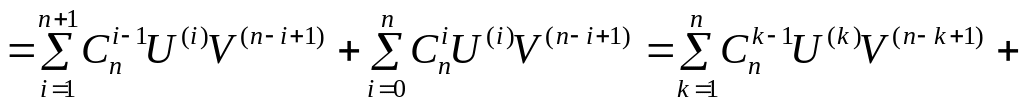
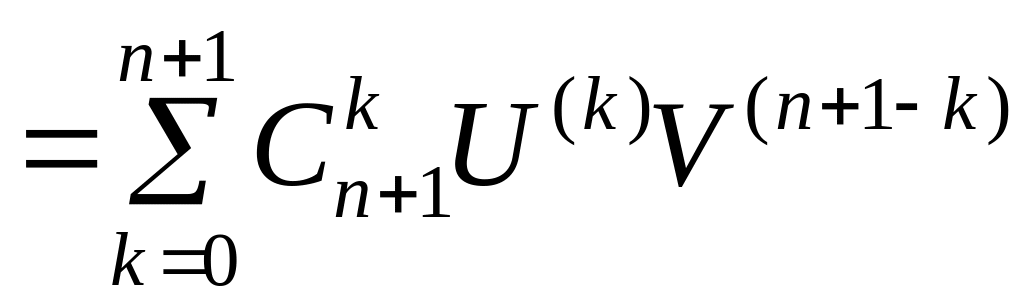Что и требовалось доказать.

Пример 4. Найти .

Решение. Воспользуемся формулой Лейбница.

.