Коэффициенты единичных перемещений

Оболочки	K1	K2	K3
Круговой цилиндр	1	1	1
Круговой конус	1	sin φ	sin φ
Сфера	1	sin φ	sin^2 φ

, , , , .

Лекция № 5

Тема: «Пластины»

Пластиной называют плоское тело, ограниченное двумя поверхностями, расстояние между которыми мало по сравнению с размерами самих поверхностей.

Срединная поверхность пластины – это поверхность равноудаленная от наружных поверхностей. Как правило, срединная поверхность представляет собой плоскость. Этим пластины отличаются от оболочек, у которых срединная поверхность не плоская. Многие детали пищевых аппаратов и машин имеют форму круглой или кольцевой пластины. В качестве примеров можно назвать плоские днища и крышки резервуаров, фланцы труб, днища роторов, центрифуги и т. д.

Инженерная теория изгиба пластин базируется на двух основных допущениях:

1. Точки, расположенные на некоторой прямой, перпендикулярной к срединной поверхности до деформации, остаются на прямой нормальной к этой поверхности после деформации пластины (гипотеза прямых нормалей Кирхгофа).

2. В плоскостях, параллельных срединной плоскости, нормальные напряжения пренебрежимо малы по сравнению с напряжениями изгиба.

При изгибе пластин, наибольший прогиб которых существенно меньше толщины, пренебрегают радиальными перемещениями точек срединной плоскости. Примем систему координат таким образом, чтобы плоскость XOY совпадала со срединной плоскостью пластины, начало координат О совместим с центром неизогнутой пластины (рис. 11).

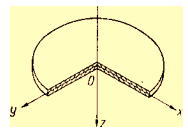
Рис. 11. Схема круглой пластины

Из рис. 12 видно, что tg φ = ± dw/dr или с учетом направления оси z и массой φ: φ = – dw/dr

Рис. 12. Схема к определению угла поворота к нормали в зависимости от прогиба

На изогнутой срединой поверхности пластины возьмем произвольную точку А (рис. 13) с координатой r и проведем через нее нормаль к поверхности. Также проведем нормаль и через ближайшую точку А', характеризуемую радиус-вектором r + dr. Длина дуги А'А' будет dr, а угол наклона этой нормали – φ + dφ.

Рис. 13. Изогнутая срединная поверхность пластины

На основании принятого допущения о недеформируемости срединной поверхности (деформации в остальных слоях пластины пропорциональны расстоянию z от срединной поверхности) для двух ближайших точек А и В (рис. 14) на расстоянии от срединной поверхности и на расстояниях r и r + dr от оси z относительное удлинение волокна АВ в радиальном направлении:

.

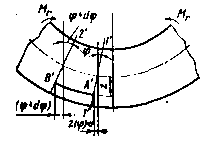
Рис. 14. Схема угловых деформаций в различных сечениях пластины

Относительное окружное удлинение в точке В можно определить, сравнивая длину соответствующих окружностей до и после деформации:

.

Вырежем из пластины бесконечно малый элемент двумя диаметральными сечениями (под углом db) и двумя концентрическими сечениями с радиусами r и r + dr (рис. 15). Выделенный элемент расположен на расстоянии z от срединной поверхности. Относительным удлинением ε_r и ε_t соответствуют нормальные напряжения σ_t и σ_r, связь между которыми (деформациями и напряжениями) определяют по обобщенному закону Гука:

, ,

где σ_t и σ_r – напряжения, действующие в радиальном и окружном направлениях; Е – модуль продольной упругости; μ – коэффициент Пуассона.

Рис. 15. Элемент пластины

При анализе вышеуказанных уравнений получим следующие выражения для определения напряжений

, .

Кроме нормальных напряжений на гранях, принадлежащих цилиндрическим сечениям выделенного элемента В₁В₁А₁А₁ и В₂В₂А₂А₂, в общем случае имеют место и касательные напряжения. Любое радиальное сечение пластины является плоскостью симметрии, следовательно, в этих сечениях касательные напряжения отсутствуют.

Переходя от нормальных напряжений σ_t и σ_r к изгибающим моментам M_t и M_r отнесенным к единице длины соответствующего сечения, получим:

, .

где D = Es³/12(1 – μ²) – цилиндрическая жесткость пластины.

Наглядно видно, что наибольшие нормальные напряжения будут при z = s/2. Поэтому:

, .