11) Производные от элементарных функций, от сложной и обратной функции, от функции заданных параметрически.

f(x) = C → 0 f(x) = xⁿ → n  x^n − 1 f(x) = sin x → cos x f(x) = cos x → − sin x f(x) = tg x → 1/cos² x f(x) = ctg x → − 1/sin² x f(x) = ln x → 1/x f(x) = log_a x → 1/(x · ln a) f(x) = e^x → e^x

Пусть функция f: [a, b] → [c, d], а функция g:[a₁, b₁] → [c₁, d₁], причём [a₁, b₁] [c, d]. Если функция f дифференцируема в точке х₀ [a, b], а функция g дифференцируема в точке y₀ = f (x₀) [a₁,b₁], то сложная функция F(x) = g( f ( x )) имеет в точке х₀ производную, равную g ' ( f ( x₀ ) )·f ' ( x₀ ).

Доказательство. Так как функция g(y) дифференцируема в точке у₀, то имеет

Δ g (y) = g ' (y₀)·Δy + δ(Δy)·Δy,

где δ(Δ х) → 0 при Δ х → 0. Так как функция f (x)дифференцируема в точке х₀, то имеем

Δ y = f ' ( x₀ )·Δx + ε (Δx)·Δx,

где ε(Δх) → 0 при Δ х → 0. Поставляя второе соотношение в первое, получим z(x) – z(x₀)=g(f(x)) – g(f(x₀))=g(y) – g(y₀)=∆y*(g’(y₀)+δ(∆y))=∆x*(g’(y₀) + δ(∆y))*(f’(x₀) + ε(∆x)).

Разделив обе части последнего соотношения на Δх, получим z(x) – z(x₀)/∆x=(g’(y₀) + δ(∆y))* (f’(x₀) + ε(∆x)).

Переходя к пределу при Δх → 0 в левой и правой части последнего равенства с учётом непрерывности рассматриваемых функций, получим

g ' ( f ( x ) )|_x0 = g ' (y₀)·f ' (x₀).

Что и требовалось доказать.

Обратная – Пусть f : [a, b] → [c, d] непрерывная, строго монотонная на интервале [a, b] функция, имеющая производную в точке х₀ [a, b]. Тогда обратная функция g = f ^-1: [c, d] →[a, b] имеет производную в точке y₀ = f(x₀) интервала [c, d] равную g’=1/f’(x₀), если f '(x₀) ≠ 0. Если f '(x₀) = 0, то g '(y₀) = + ∞ (в случае, когда f возрастает), и g '(y₀) = − ∞ (в случае, когда f убывает). Доказательство. Пусть f (x) возрастает на [a, b] и f '(x) ≠ 0. Тогда в окрестности точки y₀ = f (x₀) существует обратная функция g = f ^-1; она непрерывна и также возрастает на [c, d], в силу чего g (y) ≠ g(y₀), если у ≠ у₀. Таким образом,

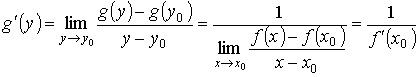
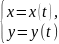tє[T₁;T₂], то y’_x=dy/dx=dy/dx*dt/dx=y’_t*t’_x=y’_t/x’_t – параметрически

12) Дифференциал, его геометрический смыл. Инвариантность дифференциала. Применение дифференциала в численных задачах.

Дифференциал функции f:R→R в точке x₀ є R может быть определён как линейная функция d_x0f(h) = f’(x₀)h, где f'(x₀) обозначает производную f в точке x₀. Таким образом df есть функция двух аргументов df : (x₀,h) → d_x0f(h). Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция d_x0f(h) линейно зависящая от h и для которой верно следующее соотношение d_x0f(h) = f(x₀ + h) – f(x₀) +o(|h|)

Дифференциа́л в математике — линейная часть приращения дифференцируемой функции или отображения. Это понятие тесно связано с понятием производной по направлению.

Пусть, как в предыдущем параграфе, y=h(u)=f(g(u))=(f₀g)(u) - сложная функция, в которой x_i=g_i(u) - промежуточные переменные. Найдём и сравним друг с другом дифференциалы функций y=f(x) и y=h(u), то есть дифференциалы величины y, вычисленные: а) в предположении, что независимыми переменными служат x₁,…,x_n; б) в предположении, что независимыми переменными служат u₁,…,u_m. В случае а) дифференциал равен dy= (x)dx₁+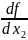 (x)dx₂+…+ (x)dx_n=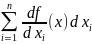 . В случае б) дифференциал, с учётом формулы для производной сложной функции, можно вычислить так: dy=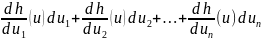 = 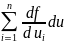_i= Полученное выражение совпадает по виду с тем, что получено для dy в п. а). Разница лишь в том, что вместо дифференциалов независимых переменных x_i теперь стоят дифференциалы функций x_i=g_i(u). Это свойство называется инвариантностью дифференциала . Оно свидетельствует о том, что формулу dy=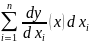 можно применять, не заботясь о том, являются ли х₁ независимыми или же промежуточными переменными.

13) Производные и дифференциалы высших порядков. f(x) f”(x)=(f’(x)) f^(K)(x)=(f^(K-1)(x)) ((1+x)^k)=m(1+x)^m-1 ((1-x)^m)”=m(m-1)(1+x)^m-1 ((1-x)^m)^(k)=m(m-1)…(m-(x-1))(1+x)^m-k

y=f(x) dy=f’(x)dx dy=d²f(x)=f”(x)dx² y=f(x) x=g(t) dy=f’(x)g’(t)dt d²y=d(dy)=d(f’(x)g’(t)dt)=(f’(x)g’(t)dt)’_tdt = (f’(x)g’(t)’_tdt² = (f”(x)g’(t)g’(t)+f’(x)g”(t))dt² = f”(x)g’(t)dt² – f’(x)g”(t)dt² = f”(x)dx² + f’(x)dx

14) Теорема Ролля. f(x) [a,b] дифференцируема на открытом промежутке (а,b), f(a)=f(b) следовательно существует хотя бы 1 точка принадлежащая [a,b] f’(c)=0. Док-во: т.к. f(x) – непрерывна на всем [a,b] то по т. Веерштрасса f(x) достигает максимума минимума в двух случаях 1) max f(x)=min f(x) const→f’(x)=0 V xє[a,b] 2) max f(x)≠min f(x) хотя бы 1 из них внутри [a,b]

15) Теорема Лангража и Коши. f(x) [a,b] дифференцируема на открытом промежутке (а,b) если существует хотя бы 1 точка принадлежащая [a,b] f’(c)=f(b)-f(a)/b-a – формула Лангранжа. Док-во: составим новую функцию, а именно разность нашей функции и хорды. y-f(a)=(f(b)-f(a)/b-a) – x-a из этого следует, что F(x)=f(x) – f(a) – (f(b) – f(a)/b-a)*(x-a) f(a)=0, f(b)=0 – попало в т. Ролля →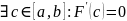 F’(x)=f’(x) f’(c) = f(b) – f(a)/a-b точка С как правило неизвестна. Частным случаем т. Л. является формула конечных преращений [a,b]=[x,x+∆x] f’(c)=f(x+∆x)-f(x)/∆x f(x+∆x)-f(x)= ∆f → ∆f=f’(c) ∆x cє[x,x+∆x]

(x) [a,b] дифференцируема на открытом промежутке (а,b) и g’(x) ≠ 0 существует “x” принадлежащая [a,b] f’(c)/g’(c) = f(b)-f(a)/g(b)-g(a) – формула Коши. Док-во: ясно, что g(b)≠g(a) иначе g(x) попадает в т. Ролля и существует с:g’(c)=0 Сост. новую функцию F(x)=f(x)-f(a)-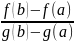 (g(x)-g(a)) f(a)=0, f(b)=0 – попало в т. Ролля → F’(x)=f’(x) - g’(x) → в точке С:0=f’(c) - g’(c) → f’(c)/f’(x) =

16) Правило Лапиталя Данное правило применимо для раскрытия неопределенности при вычислении пределов. f(x), g(x) – удовлетворяют т. Коши. Тогда если Док-во: применим к [a,x] т. Коши 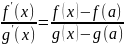= 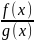устремим х→а (с→а) следовательно 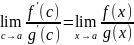Предел отношений функций может существовать, а предел отношений произведений может не быть. Поэтому рп. Лапиталя нельзя считать наоборот. Пр. Лапиталя может применяться несколько раз при этом перед каждым применением полученный предел необходимо упрощять.

17) Теорема Тейлора. In(x) In(a)=f(a) In’(a)=f’(a) Для этого будем многочлен такого вида →In(x)=e_n+e₁(x-a)+e₂(x-a)²+…+e_n(x-a)ⁿ In(a)=e_n=f(a) In’(x)=e₁+2c₂(x-a)+…+ne_n(x-c)^n-1 In’(a)=c₁=f(a) In”(x)=2c₂+3*2*c₃(x-a)+…+n(n-1)c_n(x+c)ⁿ² In”(a)=2c₂=f”(x) c_K=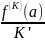

18)Монотонность ф-ции и знак ее производной Ф-ция f (x) назыв возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенствоf (x1) < f (x2).Ф-ция f (x) назыв убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, вып нер-во f (x1) > f (x2).

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке свойства монотонных ф-ций

Сумма нескольких возрастающих ф-ций является возрастающей ф-цией.

Произведение неотрицательных возрастающих ф-ций есть возрастающая ф-ция.

Если ф-ция f возрастает, то ф-ции cf (c > 0) и f + c также возрастают, а ф-ция cf (c < 0) убывает. Здесь c – некоторая константа.

Если ф-ция f возрастает и сохраняет знак, то ф-ция 1/f убывает.

Если ф-ция f возрастает и неотрицательна, то fⁿ где nN, также возрастает.

Если функция f возрастает и n – нечетное число, то f ⁿ также возрастает.

Композиция g (f (x)) возрастающих функций f и g также возрастает.

Если знак первой производной «+» ф-ция возрастает , если «-»-убывает