Нейронные сети (ИПОВС) / 4 курс - Рычагов М.Н. / Лабораторные работы / Лабораторная работа 3. Отчёт
.docxХусточка А.В. Отчёт по лабораторной работе №3 ПИН-41



Для начала создадим и обучим сеть с помощью инструментария python. Программная реализация выглядит следующим образом:
import numpy as np import numpy.random as rand import neurolab as nl from neurolab import trans import pylab as pl # Формирование входных массивов (входной массив P) и (эталоны T) N = 21 P = np.zeros((100, N)) T = np.zeros((3, 100)) x = np.array([i*0.05 for i in range(N)]) for i in range(0, 100): c = 0.9*rand.random()+0.1 a = 0.9*rand.random()+0.1 s = 0.9*rand.random()+0.1 T[0, i] = c T[1, i] = a T[2, i] = s P[i, :] = c*np.exp(-(((x-a)**2)/s)) Pt = P.transpose() # Создаем нейронную сеть net = nl.net.newff([[np.min(Pt), np.max(Pt)]]*21, [21, 15, 3], transf=[trans.LogSig(), trans.LogSig(), trans.PureLin()]) # Процесс обучения net.performFcn = 'sse' # Создаем обучающую выборку input = P target = T.transpose() error = net.train(input, target, epochs=1000, show=100, goal=0.01) # inp, tar - обучающие множества # epochs - число циклов обучения # goal - цель обучения, значение функционала ошибки при котором обучение будет завершено преждевременно # show - период вывода информации о состоянии процесса (на данный момент вывод осуществляется в консоль) # Итоги обучения (график экспоненты) pl.plot(error) pl.show() # Испытание сети p = 0.2*np.exp(-(((x-0.8)**2)/0.7)) pr = p.reshape(21, 1) out = net.sim(pr.transpose()) print('C: ', out[0, 0]) print('A: ', out[0, 1]) print('S: ', out[0, 2])
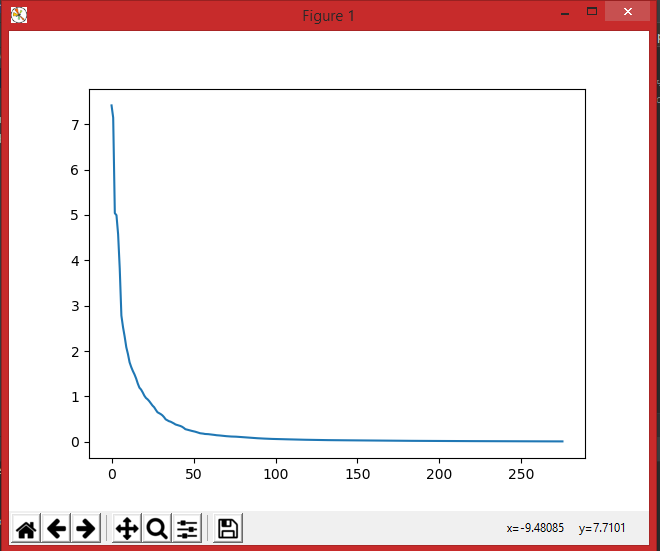
На выходе из программы мы получаем график, отображающий обучение нейронной сети.
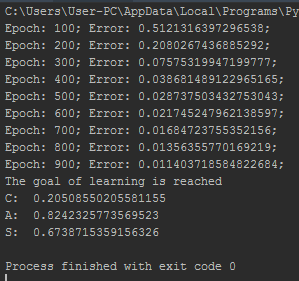
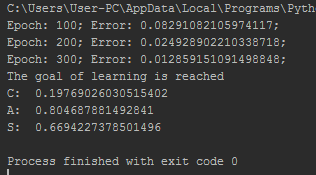
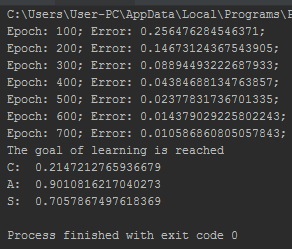
А также в процессе испытания сети мы получаем довольно точные результаты:
После того, как мы убедились, что сеть обучена, можем приступать непосредственно к выполнению задания. Для выполнения первой части задания необходимо к исходному массиву данных прибавим случайные числа из диапазонов (0 – 0.01; 0 – 0.05; 0 – 0.1; 0 -0.2).
Проверим первый диапазон:
P[i, :] = c*np.exp(-(((x-a)**2)/s)) + rand.uniform(0.0, 0.01)
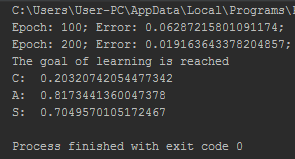
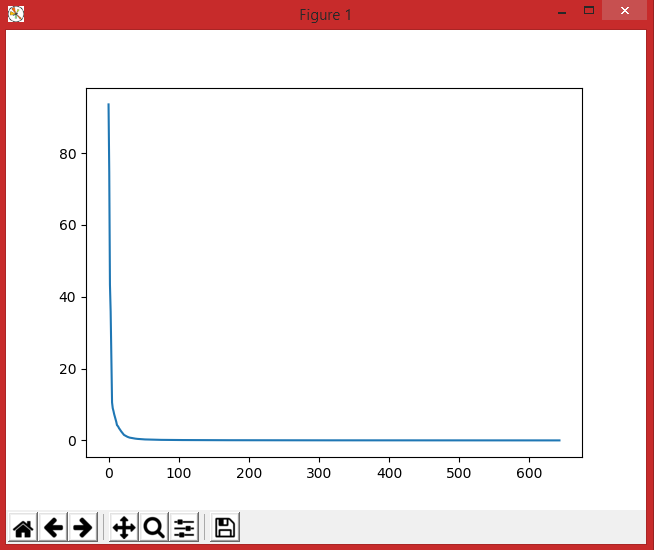
На выходе опять просмотрим график обучаемости сети:
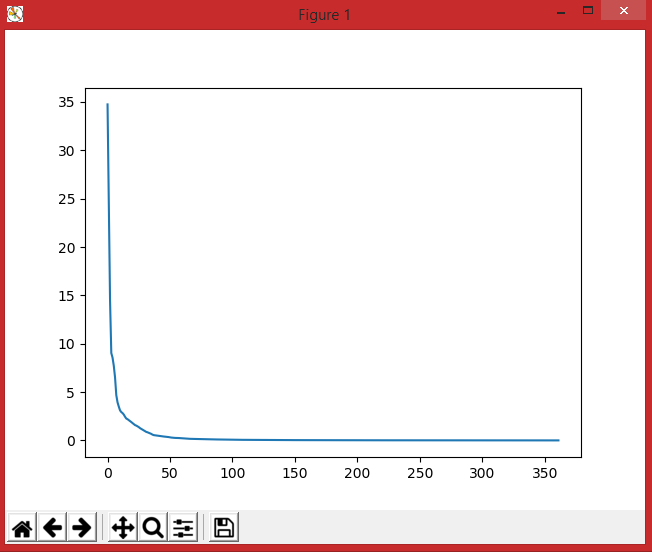
Сразу же прокомментирую вторую часть задания: на испытаниях, хоть ошибок при обучении было и больше, но значения всё равно подобраны довольно близко. Вероятно, это связано с тем, что шум, добавленный к исходному массиву был выбран из довольно маленького диапазона.
Проверим второй диапазон:
P[i, :] = c * np.exp(-(((x - a) ** 2) / s)) + rand.uniform(0.0, 0.05)
На выходе опять просмотрим график обучаемости сети:
Сразу же прокомментирую вторую часть задания: на испытаниях, хоть ошибок при обучении было и больше, но значения всё равно подобраны довольно близко. Вероятно, это связано с тем, что шум, добавленный к исходному массиву был выбран из довольно маленького диапазона.
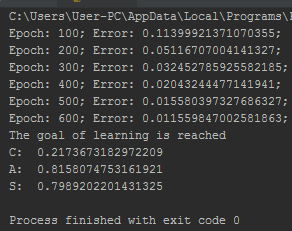
Проверим третий диапазон:
P[i, :] = c * np.exp(-(((x - a) ** 2) / s)) + rand.uniform(0.0, 0.1)
На выходе опять просмотрим график обучаемости сети:
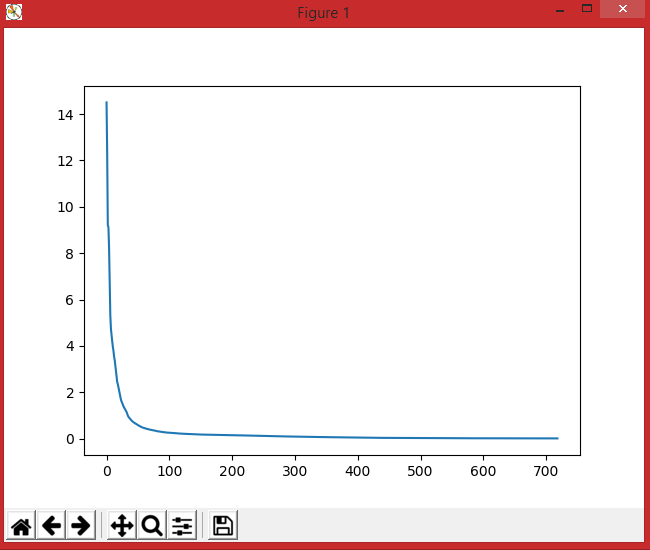
Сразу же прокомментирую вторую часть задания: в этом случае диапазон шума в больших границах, потому и в значениях уже присутствуют ошибки на 0,1 (в коэффициенте A).
Проверим четвёртый диапазон:
P[i, :] = c * np.exp(-(((x - a) ** 2) / s)) + rand.uniform(0.0, 0.2)
На выходе опять просмотрим график обучаемости сети:
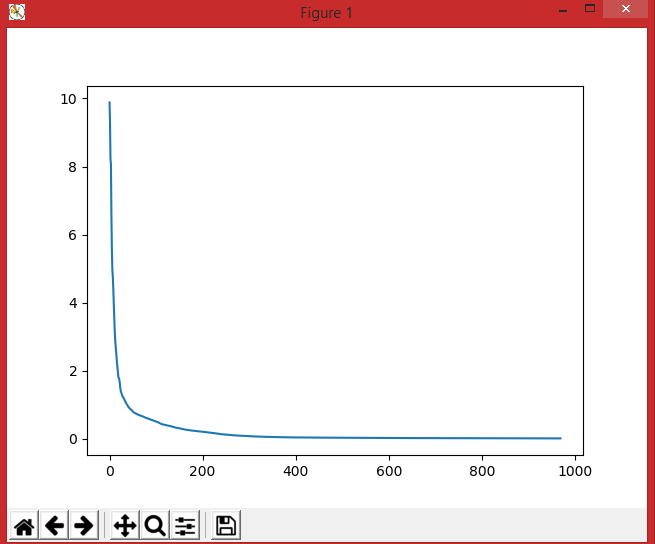
Сразу же прокомментирую вторую часть задания: в этом случае диапазон шума в больших границах, потому и в значениях уже присутствуют ошибки на 0,1 (в коэффициенте S).