14

Лабораторная работа.

Московский Институт Электронной Техники

Кафедра ИПОВС

"УТВЕРЖДАЮ"

Зав.кафедрой ИПОВС

Нестеров А.Э.

ЛАБОРАТОРНАЯ РАБОТА

Оптимизация режимов нелинейного объекта управления.

Разработал:

Доцент Трояновский В.М.

Москва 2002 г.

СОДЕРЖАНИЕ

1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ 3

1.1. Введение. 3

1.2. Безинерционный объект с одним входом 4

1.3. Влияние линейной инерционной части 9

1.4. Объект с двумя независимыми входами. 10

2. Средства моделирования. 10

2.1. Возможности средств моделирования. 10

2.2. Формирование входных сигналов. 11

2.3. Руководство пользователя к программе EXTREM.EXE. 11

3. Задание к лабораторной работе. 13

1. Теоретические сведения

1.1. Введение.

Оптимизация работы технологических объектов является одной из важнейших задач систем управления. Для нелинейных объектов управления такая задача сводится к определению наилучших значений параметров, доступных для воздействия; при этом некоторый критерий эффективности достигает экстремума (максимума или минимума). Для решения задачи оптимизации мало знать, что объект имеет экстремальную характеристику – надо уметь определять текущее состояние объекта, рассчитывать необходимые управляющие воздействия и, наконец, наилучшим образом стабилизировать объект в близи экстремума.

Среди многочисленных идей и методов изучения характеристик объекта управления им наиболее привлекательна идея дуального управления, выдвинутая в 50-х годах А.А. Фельдбаумом. Можно использовать данные нормального функционирования объекта (т.е. случайные флуктуации, всегда наблюдаемые у входных и выходных сигналов) для изучения текущих характеристик объекта и расчета управляющих воздействий, а отклик объекта на управляющее воздействие уточняет полученные данные. Использование случайных сигналов, наличие нелинейностей и возможных динамических связей в объектах, а также воздействие помех требуют привлечения соответствующих статистических методов обработки сигналов в задаче дуального управления.

В общем случае модель управляемого динамического нелинейного объекта представляют в виде рис.1.

Как следует из представленной схемы, объект может иметь целый реестр входных и выходных сигналов, содержать линейную инерционную часть и нелинейный преобразователь сигналов, недоступную для наблюдения помеху. При этом критерий эффективности может рассчитываться на основании доступных для измерения сигналов на входе и выходе объекта, а для формирования управляющего воздействия могут использоваться как текущие значения доступных сигналов, так и накапливаемые данные.

1.2. Безинерционный объект с одним входом

В простейшем случае, когда объект управления содержит только нелинейную безинерционную часть (весовая функция линейной инерционной части при этом вырождается в дельта-функцию) и единственный вход и выход, схема рис.1 преобразуется к виду рис. 2.

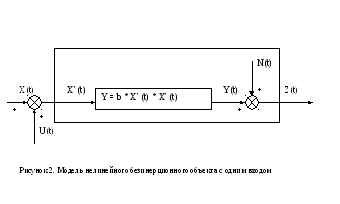
При наличии неизвестного заранее смещения экстремума на величину Uopt:

Y=b*(X'(t) – Uopt)², (1)

где

X'(t)=X(t) + U(t) (2)

отражает возможность параболической аппроксимации вблизи экстремума зависимости критерия эффективности от входного воздействия. Следует отметить также, что на практике распределение амплитуд входного сигнала X(t) обычно близко к нормальному (гауссовскому) распределению. Будем полагать, что входной сигнал – стационарный и эргодический и его математическое ожидание равно нулю, а используемые отсчеты некоррелированы.

M {X (t)} = 0,

K_xx(τ) = M {X(t)*X(t+τ)} = δ (τ)*σ_x² (3)

Предполагается, что помеха N(t) также имеет нулевое математическое ожидание, конечную дисперсию и не зависит от входного сигнала.

M {N(t)} = 0,

M {N(t)*N(t)} = σ²_n, (4)

M {X(t)*N(t)} = 0.

В качестве критерия эффективности будем рассматривать среднее значение выходного сигнала Z(t), что можно интерпретировать как средние потери относительно минимально возможного уровня. Тогда при некотором фиксированном значении управляющего сигнала U(t) = U’

F=M{Z(t)}=M{Y(t)+N(t)}=M{b*(X(t)+U’-Uopt)²+N(t)}=

=b*M{X(t)²}+2b*M{X(t)*(U’-Uopt)}+b*(U’-Upot)²+M{N(t)}=

=b*σ_x²+b*(U’-Uopt)² (5)

Таким образом, потери тем больше, чем больше дисперсия дисперсия входного сигнала и чем больше отклонение управляющего воздействия U’ от неизвестного заранее Uopt.

Вместе с этим, из (1), (2) следует:

dY = 2b * (X + U(t) - Uopt) * dX ≈ 2b * (U’ - Uopt) * dX, (6)

т.к. при наблюдении за объектом U(t)=U’=const и |U’|>>|X|;

или в другом виде

dY/dX = 2b * ( U’ – Uopt). (7)

Т.е. градиент нелинейности в рабочей точке U = U’ прямо пропорционален величиен смещения управляющего сигнала от оптимума и завмсит таким же образом от второго неизвестного заранее параметра “b”, который можно трактовать как крутизну нелинейности, что следует из (1), (2):

d²Y/dx² = 2*b.

Таким образом, для функции Y(X’) и ее производных имеем (см. рис.3.):

y

Из представленных графиков видно, что оптимальное управление легко организовать, опираясь на градиент, т.к. в отличие от самой функции, градиент меняет знак при переходе X’ через оптимум и линейно зависит от управляющего воздействия. Более того, если определить величину второй производной (которая в данном случае постоянна при любом значении входа), становится возможным расчет Uopt по текущему значению управляющего воздействия и величине градиента функции в этой точке.

Так как сигнал Y(t) не доступен для измерения, приходится пользоваться «зашумленным» сигналом Z(t) с тем, чтобы получить оценки интересующих нас параметров – в первую очередь градиента. Известно, что наилучшую оценку градиента (с точки зрения метода наименьших квадратов) в рассматриаваемых условиях дает следующее расчетное соотношение:

K = 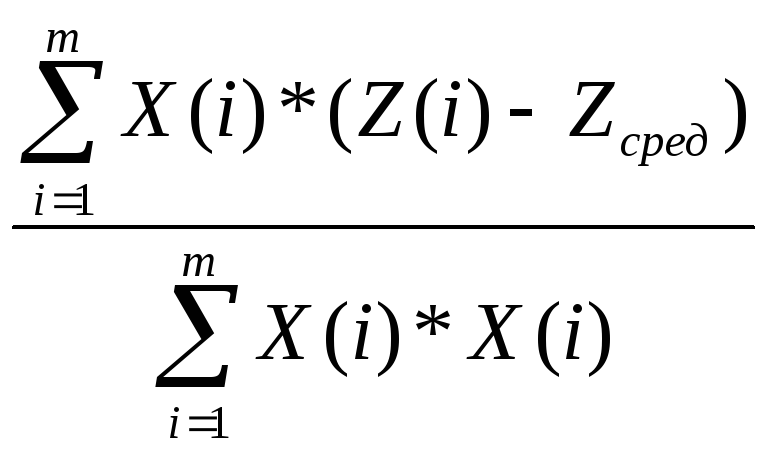i=1, 2,…, m (8)

где m- число независимых отсчетов, Z_сред – среднее значение доступного входного сигнала.

При этом рассчитываемая величина K является несмещенной оценкой градиента, а ее дисперсия при линеаризуемости в малом определяется как

(9)

Поскольку значение параметра «b» априорно неизвестно, движение к экстремуму вначале организуют, опираясь лишь на знак градиента и рассчитывая величину управляющего воздействия на очередном шаге «p» как

dU(p) = sign(K)*a(p), (10)

где

a(p) = 3σ_x/p. (11)

Применение стратегии выбора величины a(p) по соотношению (11) гарантирует сходимость алгоритма, но явно замедляет движение с ростом числа шагов. Поэтому следующий этап дуального управления состоит в том, чтобы определить оценку параметра «b», опираясь на результаты движения, осуществляемого указанным выше способом. Очевидно, при этом можно вновь использовать метод наименьших квадратов (или более примитивный метод прямого усреднения частных оценок), только в иной системе координат (Рисунок 4). В качестве данных берется Таблица 1.

Номер шага	^ k	dU	dk
1 2 . . r

Табл. 1

Данные из эксперимента

В простейшем случае рассчитывается оценка параметра «b» и средний квадрат этой оценки:

b_j = dkj / dUj, j = 1..r; b' = (12)

σ²_b = (13)

Завершающим этапом дуального управления является определение оптимального уровня сохранения флуктуаций входного сигнала вблизи экстремума.

Проблема состоит в следующем. Как следует из (5), потери тем меньше, чем меньше σ_x. Однако свести σ_x к нулю нельзя, т.к. флуктуации X(t) используются в качестве поискового сигнала для определения градиента в соответствии с соотношением (8). Если известна оценка параметра «b», то управляющее воздействие рассчитывается в соответствии с (7), (8) как

dU = -k / 2b (14)

Такое управляющее воздействие вывело бы объект прямо к экстремуму, будь точными оценки параметров «K» и «b». В силу того, что оценка градиента K имеет дисперсию, величина которой определяется соотношением (9) и не зависит от положения рабочей точки (абсолютного значения управляющего сигнала U), то из (9), (14) с очевидностью следует такое соотношение:

σ_u² = 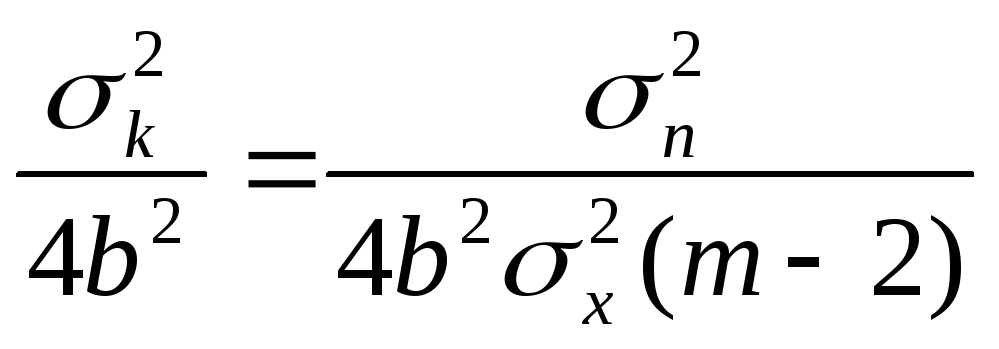(15)

при этом соотношение (5) преобразуется к виду:

F = 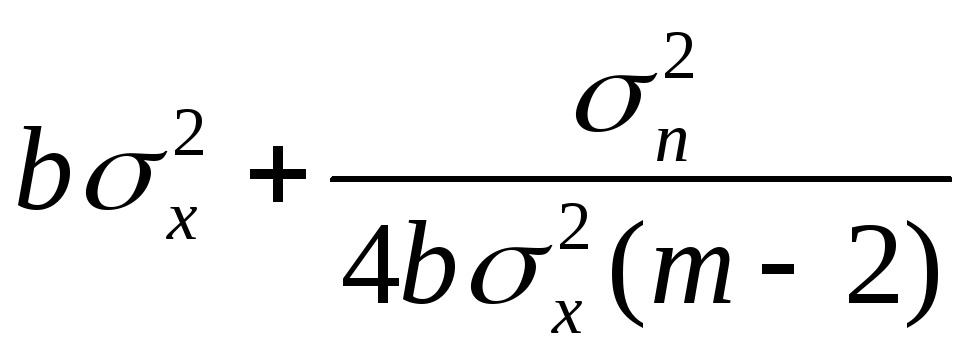(формула 16)

Нетрудно увидеть, что функция F() экстремальна:

(17)

(18)

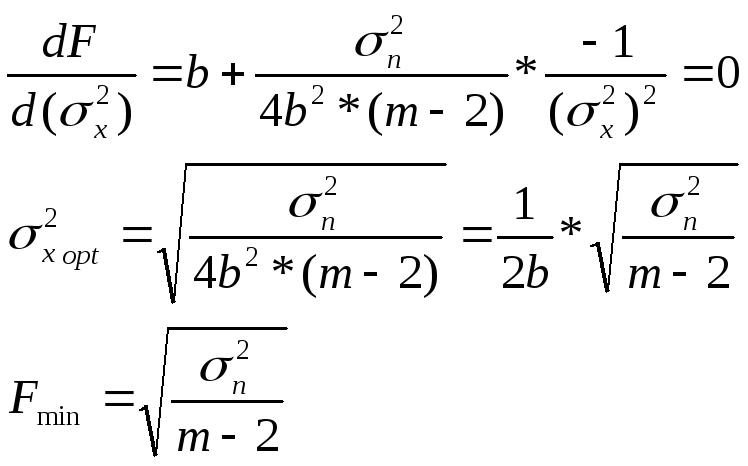
Таким образом соотношение (17) позволяет замкнуть цепочку в изучении характеристик объекта при ступенчато-непрерывном дуальном управлении: после определения оценки параметра "b" и эмпирического исследования зависимости F(σ_x²) с целью определения σ²_xopt при некотором фиксированном "m" (число отсчетов, используемых при расчете оценки градиента k), становится возможным определение и последнего неизвестного параметра – дисперсии помехи σ_n². Заметим, что для рассматриваемой модели объекта оценку величины σ_n² легко получить и в любой другой точке вдоль траектории управления: достаточно на некоторое время прекратить подачу сигнала X(t), застабилизировать текущее значение U(t) и измерить степень флуктуаций выходного сигнала Z(t). Поэтому возможны различные подходы к определению конечного эффекта дуального управления как в части приведения объекта к экстремуму, так и в части определения неизвестного параметра объекта "b".